Horizontal Projectile
Category : NEET
Horizontal Projectile
A body be projected horizontally from a certain height ?y? vertically above the ground with initial velocity u. If friction is considered to be absent, then there is no other horizontal force which can affect the horizontal motion. The horizontal velocity therefore remains constant and so the object covers equal distance in horizontal direction in equal intervals of time.
(1) Trajectory of horizontal projectile: The horizontal displacement x is governed by the equation
\[x\text{ }=\text{ }ut\,\,\,\,\Rightarrow \,\,t=\frac{x}{u}\] ?. (i)
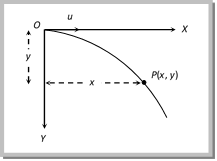
The vertical displacement y is governed by \[y=\frac{1}{2}g{{t}^{2}}\] ?. (ii)
(since initial vertical velocity is zero)
By substituting the value of t in equation (ii) \[y=\frac{1}{2}\frac{g\,{{x}^{2}}}{{{u}^{2}}}\]
Sample problems based on trajectory
Problem 66. An aeroplane is flying at a constant horizontal velocity of 600 km/hr at an elevation of 6 km towards a point directly above the target on the earth?s surface. At an appropriate time, the pilot releases a ball so that it strikes the target at the earth. The ball will appear to be falling [MP PET 1993]
(a) On a parabolic path as seen by pilot in the plane
(b) Vertically along a straight path as seen by an observer on the ground near the target
(c) On a parabolic path as seen by an observer on the ground near the target
(d) On a zig-zag path as seen by pilot in the plane
Solution: (c)
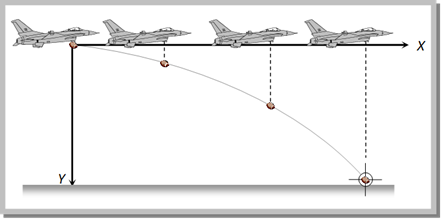
The path of the ball appears parabolic to a observer near the target because it is at rest. But to a Pilot the path appears straight line because the horizontal velocity of aeroplane and the ball are equal, so the relative horizontal displacement is zero.
Problem 67. The barrel of a gun and the target are at the same height. As soon as the gun is fired, the target is also released. In which of the following cases, the bullet will not strike the target
(a) Range of projectile is less than the initial distance between the gun and the target
(b) Range of projectile is more than the initial distance between the gun and the target
(c) Range of projectile is equal to the initial distance between the gun and target
(d) Bullet will always strike the target
Solution: (a) Condition for hitting of bullet with target initial distance between the gun and target \[\le \]Range of projectile.
Problem 68. A ball rolls off top of a staircase with a horizontal velocity u m/s. If the steps are h metre high and b mere wide, the ball will just hit the edge of nth step if n equals to
(a) \[\frac{h{{u}^{2}}}{g{{b}^{2}}}\] (b) \[\frac{{{u}^{2}}8}{g{{b}^{2}}}\] (c) \[\frac{2h{{u}^{2}}}{g{{b}^{2}}}\] (d) \[\frac{2{{u}^{2}}g}{h{{b}^{2}}}\].
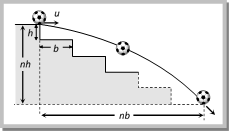
Solution: (c) By using equation of trajectory \[y=\frac{g{{x}^{2}}}{2{{u}^{2}}}\] for given condition
\[nh=\frac{g{{(nb)}^{2}}}{2{{u}^{2}}}\therefore \,\,n=\frac{2h{{u}^{2}}}{g{{b}^{2}}}\]
(2) Displacement of Projectile \[\mathbf{(}\vec{r}\mathbf{)}\]: After time t, horizontal displacement \[x=ut\] and vertical displacement \[y=\frac{1}{2}g{{t}^{2}}\].
So, the position vector \[\vec{r}=ut\,\hat{i}-\frac{1}{2}g{{t}^{2}}\,\hat{j}\]
Therefore \[r=ut\,\sqrt{1+{{\left( \frac{gt}{2u} \right)}^{2}}}\] and \[\alpha =\,{{\tan }^{-1}}\left( \frac{gt}{2u} \right)\]
\[\alpha ={{\tan }^{-1}}\left( {\sqrt{\frac{gy}{2}}}/{u}\; \right)\] \[\left( \text{as}\,\,t=\sqrt{\frac{2y}{g}} \right)\]
(3) Instantaneous velocity: Throughout the motion, the horizontal component of the velocity is \[{{\operatorname{v}}_{x}}= u\].
The vertical component of velocity increases with time and is given by
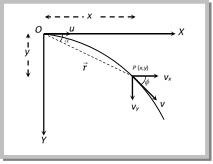
\[{{\operatorname{v}}_{y}}= 0 + g t = g t\] (From \[\operatorname{v} = u + g t\])
So, \[\vec{v}={{v}_{x}}\hat{i}-{{v}_{y}}\hat{j}=\vec{v}=u\,\hat{i}-g\,t\,\hat{j}\]
i.e. \[v=\sqrt{{{u}^{2}}+{{\left( gt \right)}^{2}}}=\,u\sqrt{1+{{\left( \frac{gt}{u} \right)}^{2}}}\]
Again \[\vec{v}=u\hat{i}-\sqrt{2gy}\,\hat{j}\]
i.e. \[v=\sqrt{{{u}^{2}}+2gy}\]
Direction of instantaneous velocity: \[\tan \,\varphi =\frac{{{v}_{y}}}{{{v}_{x}}}\Rightarrow \varphi ={{\tan }^{-1}}\left( \frac{{{v}_{y}}}{{{v}_{x}}} \right)={{\tan }^{-1}}\left( \frac{\sqrt{2gy}}{u} \right)\] or \[\varphi ={{\tan }^{-1}}\left( \frac{gt}{u} \right)\]
Where \[\phi \] is the angle of instantaneous velocity from the horizontal.
Sample problems based on velocity
Problem 69. A body is projected horizontally from the top of a tower with initial velocity \[18 m{{s}^{1}}\]. It hits the ground at angle\[{{45}^{o}}\]. What is the vertical component of velocity when it strikes the ground
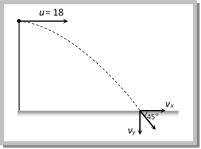
(a) \[9 m{{s}^{1}}\] (b) \[9\sqrt{2}~m{{s}^{1}}\] (c) \[18\text{ }m{{s}^{1}}\] (d) \[18\sqrt{2}\,m{{s}^{1}}\]
Solution: (c) When the body strikes the ground
\[\tan {{45}^{o}}\,=\frac{{{v}_{y}}}{{{v}_{x}}}=\frac{{{v}_{y}}}{18}=\text{ }1\]
\[{{v}_{y}}=18\,m/s.\]
Problem 70. A man standing on the roof of a house of height h throws one particle vertically downwards and another particle horizontally with the same velocity u. The ratio of their velocities when they reach the earth?s surface will be
(a) \[\sqrt{2gh+{{u}^{2}}}\,:\,\,u\] (b) 1 : 2 (c) 1 : 1 (d) \[\sqrt{2gh+{{u}^{2}}}\,\,:\,\,\,\sqrt{2gh}\]
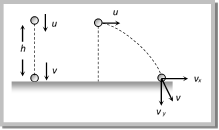
Solution: (c) For first particle: \[{{v}^{2}}={{u}^{2}}+2gh\Rightarrow v=\sqrt{{{u}^{2}}+2gh}\]
For second particle: \[v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{{{u}^{2}}+{{\left( \sqrt{2gh} \right)}^{2}}}=\sqrt{{{u}^{2}}+2gh}\]
So the ratio of velocities will be 1 : 1.
Problem 71. A staircase contains three steps each 10 cm high and 20 cm wide. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane
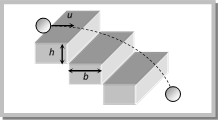
(a) 0.5 m/s (b) 1 m/s (c) 2 m/s (d) 4 m/s
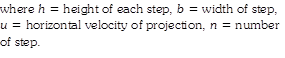Solution: (c) Formula for this condition is given by \[\,\,n=\frac{2h{{u}^{2}}}{g{{b}^{2}}}\]
\[\Rightarrow 3=\frac{2\times 10\times {{u}^{2}}}{10\times {{20}^{2}}}\,\Rightarrow \,{{u}^{2}}=200\,cm/sec=2\,m/sec\]
(4) Time of Flight: If a body is projected horizontally from a height h with velocity u and time taken by the body to reach the ground is T, then
\[h=0+\frac{1}{2}g{{T}^{2}}\] (for vertical motion)
\[T=\sqrt{\frac{2h}{g}}\]
Sample problems based on time of flight
Problem 72. Two bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit the ground first [Orissa JEE 2003]
(a) The faster one (b) Depends on their mass
(c) The slower one (d) Both will reach simultaneously
Solution: (d)
Problem 73. An aeroplane is flying at a height of 1960 m in horizontal direction with a velocity of 360 km/hr. When it is vertically above the point. A on the ground, it drops a bomb. The bomb strikes a point B on the ground, then the time taken by the bomb to reach the ground is
(a) \[20\sqrt{2}\] sec (b) 20 sec (c) \[10\sqrt{2}\,\,\sec \] (d) 10 sec
Solution: (b) \[t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times 1960}{9.8}}=\text{ }20\text{ }sec\]
You need to login to perform this action.
You will be redirected in
3 sec
