Maximum Height
Category : NEET
Maximum Height Maximum height: It is the maximum height from the point of projection, a projectile can reach. 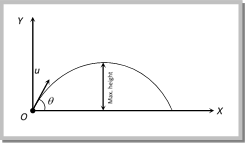 So, by using \[{{v}^{2}}={{u}^{2}}+2as\] \[0={{(u\sin \theta )}^{2}}-2gH\] \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] (i) Maximum height can also be expressed as \[H=\frac{u_{y}^{2}}{2g}\] (where \[{{u}_{y}}\] is the vertical component of initial velocity). (ii) \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}\] (when \[{{\sin }^{2}}\,\theta = max = 1\] i.e., \[\theta = 9{{0}^{o}}\]) i.e., for maximum height body should be projected vertically upward. So it falls back to the point of projection after reaching the maximum height. (iii) For complementary angles of projection \[\theta \,\,and\, 9{{0}^{o}}\theta \] Ratio of maximum height = \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta /2g}{{{u}^{2}}{{\sin }^{2}}({{90}^{o}}-\theta )2g}\] \[=\frac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }\] \[={{\tan }^{2}}\theta \] \[\therefore \,\,\,\,\,\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta \] Sample problem based on maximum height Problem 49. A cricketer can throw a ball to a maximum horizontal distance of 100 m. With the same effort, he throws the ball vertically upwards. The maximum height attained by the ball is [UPSEAT 2002] (a) 100 m (b) 80 m (c) 60 m (d) 50 m Solution: (d) \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=100\,m\] (when \[\theta =45{}^\circ \]) \[\therefore \,\,\,\,\,{{u}^{2}}=100\times 10=1000\] \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}=\frac{1000}{2\times 10}=50\,\,metre.\] (when \[\theta =90{}^\circ \]) Problem 50. A ball thrown by one player reaches the other in 2 sec. the maximum height attained by the ball above the point of projection will be about [Pb. PMT 2002] (a) 10 m (b) 7.5 m (c) 5 m (d) 2.5 m Solution: (c) \[T=\frac{2u\sin \theta }{g}=2\,sec\] (given) \[\therefore \,\,\,\,\,u\sin \theta =10\] Now \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{(10)}^{2}}}{2\times 10}=5\,m.\] Problem 51. Two stones are projected with the same magnitude of velocity, but making different angles with horizontal. The angle of projection of one is p/3 and its maximum height is Y, the maximum height attained by the other stone with as p/6 angle of projection is [J & K CET 2000] (a) Y (b) 2 Y (c) 3 Y (d) \[\frac{Y}{3}\] Solution: (d) When two stones are projected with same velocity then for complementary angles \[\theta \] and \[(9{{0}^{o}}\theta )\] Ratio of maximum heights: \[\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta ={{\tan }^{2}}\frac{\pi }{3}=3\Rightarrow {{H}_{2}}=\frac{{{H}_{1}}}{3}=\frac{Y}{3}\] Problem 52. If the initial velocity of a projectile be doubled. Keeping the angle of projection same, the maximum height reached by it will (a) Remain the same (b) Be doubled (c) Be quadrupled (d) Be halved Solution: (c) \[H=\frac{{{u}^{2}}\sin 2\theta }{2g}\] \[\therefore \,\,\,\,H\propto {{u}^{2}}\] [As \[\theta =cons\tan t\]] If initial velocity of a projectile be doubled then H will becomes 4 times. Problem 53. Pankaj and Sudhir are playing with two different balls of masses m and 2m respectively. If Pankaj throws his ball vertically up and Sudhir at an angle \[\theta \], both of them stay in our view for the same period. The height attained by the two balls are in the ratio (a) 2 : 1 (b) 1 : 1 (c) \[1:cos\,\theta \] (d) \[1:sec\,\theta \]
So, by using \[{{v}^{2}}={{u}^{2}}+2as\] \[0={{(u\sin \theta )}^{2}}-2gH\] \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] (i) Maximum height can also be expressed as \[H=\frac{u_{y}^{2}}{2g}\] (where \[{{u}_{y}}\] is the vertical component of initial velocity). (ii) \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}\] (when \[{{\sin }^{2}}\,\theta = max = 1\] i.e., \[\theta = 9{{0}^{o}}\]) i.e., for maximum height body should be projected vertically upward. So it falls back to the point of projection after reaching the maximum height. (iii) For complementary angles of projection \[\theta \,\,and\, 9{{0}^{o}}\theta \] Ratio of maximum height = \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta /2g}{{{u}^{2}}{{\sin }^{2}}({{90}^{o}}-\theta )2g}\] \[=\frac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }\] \[={{\tan }^{2}}\theta \] \[\therefore \,\,\,\,\,\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta \] Sample problem based on maximum height Problem 49. A cricketer can throw a ball to a maximum horizontal distance of 100 m. With the same effort, he throws the ball vertically upwards. The maximum height attained by the ball is [UPSEAT 2002] (a) 100 m (b) 80 m (c) 60 m (d) 50 m Solution: (d) \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=100\,m\] (when \[\theta =45{}^\circ \]) \[\therefore \,\,\,\,\,{{u}^{2}}=100\times 10=1000\] \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}=\frac{1000}{2\times 10}=50\,\,metre.\] (when \[\theta =90{}^\circ \]) Problem 50. A ball thrown by one player reaches the other in 2 sec. the maximum height attained by the ball above the point of projection will be about [Pb. PMT 2002] (a) 10 m (b) 7.5 m (c) 5 m (d) 2.5 m Solution: (c) \[T=\frac{2u\sin \theta }{g}=2\,sec\] (given) \[\therefore \,\,\,\,\,u\sin \theta =10\] Now \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{(10)}^{2}}}{2\times 10}=5\,m.\] Problem 51. Two stones are projected with the same magnitude of velocity, but making different angles with horizontal. The angle of projection of one is p/3 and its maximum height is Y, the maximum height attained by the other stone with as p/6 angle of projection is [J & K CET 2000] (a) Y (b) 2 Y (c) 3 Y (d) \[\frac{Y}{3}\] Solution: (d) When two stones are projected with same velocity then for complementary angles \[\theta \] and \[(9{{0}^{o}}\theta )\] Ratio of maximum heights: \[\frac{{{H}_{1}}}{{{H}_{2}}}={{\tan }^{2}}\theta ={{\tan }^{2}}\frac{\pi }{3}=3\Rightarrow {{H}_{2}}=\frac{{{H}_{1}}}{3}=\frac{Y}{3}\] Problem 52. If the initial velocity of a projectile be doubled. Keeping the angle of projection same, the maximum height reached by it will (a) Remain the same (b) Be doubled (c) Be quadrupled (d) Be halved Solution: (c) \[H=\frac{{{u}^{2}}\sin 2\theta }{2g}\] \[\therefore \,\,\,\,H\propto {{u}^{2}}\] [As \[\theta =cons\tan t\]] If initial velocity of a projectile be doubled then H will becomes 4 times. Problem 53. Pankaj and Sudhir are playing with two different balls of masses m and 2m respectively. If Pankaj throws his ball vertically up and Sudhir at an angle \[\theta \], both of them stay in our view for the same period. The height attained by the two balls are in the ratio (a) 2 : 1 (b) 1 : 1 (c) \[1:cos\,\theta \] (d) \[1:sec\,\theta \] 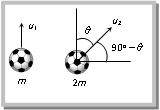 Solution: (b) Time of flight for the ball thrown by Pankaj \[{{T}_{1}}=\frac{2{{u}_{1}}}{g}\] Time of flight for the ball thrown by Sudhir \[{{T}_{2}}=\frac{2{{u}_{2}}\sin ({{90}^{o}}-\theta )}{g}=\frac{2{{u}_{2}}\cos \theta }{g}\] According to problem \[{{T}_{1}}={{T}_{2}}\Rightarrow \frac{2{{u}_{1}}}{g}=\frac{2{{u}_{2}}\cos \theta }{g}\Rightarrow {{u}_{1}}={{u}_{2}}\cos \theta \] Height of the ball thrown by Pankaj \[{{H}_{1}}=\frac{u_{1}^{2}}{2g}\] Height of the ball thrown by Sudhir \[{{H}_{2}}=\frac{u_{2}^{2}{{\sin }^{2}}({{90}^{o}}-\theta )}{2g}\]\[=\frac{u_{2}^{2}{{\cos }^{2}}\theta }{2g}\] \ \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{u_{1}^{2}/2g}{u_{2}^{2}{{\cos }^{2}}\theta /2g}\] = 1 [As \[{{u}_{1}}={{u}_{2}}\cos \theta \]] Short Trick: Maximum height H µ T2 \[\frac{{{H}_{1}}}{{{H}_{2}}}={{\left( \frac{{{T}_{1}}}{{{T}_{2}}} \right)}^{2}}\]. \ \[\frac{{{H}_{1}}}{{{H}_{2}}}=1\] (As \[{{T}_{1}}={{T}_{2}}\]) Problem 54. A boy aims a gun at a bird from a point, at a horizontal distance of 100 m. If the gun can impart a velocity of \[500 m{{s}^{1}}\] to the bullet. At what height above the bird must he aim his gun in order to hit it (take \[\operatorname{g} = 10 m{{s}^{2}}\]) [CPMT 1996] (a) 20 cm (b) 10 cm (c) 50 cm (d) 100 cm Solution: (a) Time taken by bullet to travel a horizontal distance of 100 m is given by \[t=\frac{100}{500}=\frac{1}{5}sec\] In this time the bullet also moves downward due to gravity its vertical displacement \[h=\frac{1}{2}g\,{{t}^{2}}=\frac{1}{2}\times 10\times {{\left( \frac{1}{5} \right)}^{2}}\]\[=1/5\,m= 20 cm\] So bullet should be fired aiming 20 cm above the bird to hit it. Problem 55. The maximum horizontal range of a projectile is 400 m. The maximum height attained by it will be (a) 100 m (b) 200 m (c) 400 m (d) 800 m Solution: (a) \[{{R}_{\max }}=400\,m\] [when \[\theta =45{}^\circ \]] So from the Relation \[R=4H\cot \theta \Rightarrow 400=4H\cot 45{}^\circ \Rightarrow \,H=100\,m.\] Problem 56. Two bodies are projected with the same velocity. If one is projected at an angle of \[{{30}^{o}}\] and the other at an angle of \[{{60}^{o}}\] to the horizontal, the ratio of the maximum heights reached is [EAMCET (Med.) 1995; Pb. PMT 2000; AIIMS 2001] (a) 3 : 1 (b) 1 : 3 (c) 1 : 2 (d) 2 : 1 Solution: (b) \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{{{\sin }^{2}}{{\theta }_{1}}}{{{\sin }^{2}}{{\theta }_{2}}}=\frac{{{\sin }^{2}}{{30}^{o}}}{{{\sin }^{2}}{{60}^{o}}}=\frac{1}{3}\] Problem 57. If time of flight of a projectile is 10 seconds. Range is 500 m. The maximum height attained by it will be [RPMT 1997; RPET 1998] (a) 125 m (b) 50 m (c) 100 m (d) 150 m Solution: (a) \[T=\frac{2u\sin \theta }{g}=10\,\sec \Rightarrow \,u\sin \theta =50\] so \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{(50)}^{2}}}{2\times 10}=125\,m\]. Problem 58. A man can throw a stone 80 m. The maximum height to which he can raise the stone is (a) 10 m (b) 15 m (c) 30 m (d) 40 m Solution: (d) The problem is different from problem no. (54). In that problem for a given angle of projection range was given and we had find maximum height for that angle. But in this problem angle of projection can vary, \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=80\,m\] [for \[\theta =45{}^\circ \]] But height can be maximum when body projected vertically up \[{{H}_{\max }}=\frac{{{u}^{2}}{{\sin }^{2}}{{90}^{o}}}{2g}=\frac{{{u}^{2}}}{2g}=\frac{1}{2}\left( \frac{{{u}^{2}}}{g} \right)=40\,m\] Problem 59. A ball is thrown at different angles with the same speed u and from the same points and it has same range in both the cases. If \[{{y}_{1}}and\text{ }{{y}_{2}}\] be the heights attained in the two cases, then \[{{y}_{1}}+{{y}_{2}}=\] (a) \[\frac{{{u}^{2}}}{g}\] (b) \[\frac{2{{u}^{2}}}{g}\] (c) \[\frac{{{u}^{2}}}{2g}\] (d) \[\frac{{{u}^{2}}}{4g}\] Solution (c) Same ranges can be obtained for complementary angles i.e. \[\theta \] and \[{{90}^{o}}\theta \] \[{{y}_{1}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[{{y}_{2}}=\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}\] \[\therefore \,\,\,\,{{y}_{1}}+{{y}_{2}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}+\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}=\frac{{{u}^{2}}}{2g}\]
Solution: (b) Time of flight for the ball thrown by Pankaj \[{{T}_{1}}=\frac{2{{u}_{1}}}{g}\] Time of flight for the ball thrown by Sudhir \[{{T}_{2}}=\frac{2{{u}_{2}}\sin ({{90}^{o}}-\theta )}{g}=\frac{2{{u}_{2}}\cos \theta }{g}\] According to problem \[{{T}_{1}}={{T}_{2}}\Rightarrow \frac{2{{u}_{1}}}{g}=\frac{2{{u}_{2}}\cos \theta }{g}\Rightarrow {{u}_{1}}={{u}_{2}}\cos \theta \] Height of the ball thrown by Pankaj \[{{H}_{1}}=\frac{u_{1}^{2}}{2g}\] Height of the ball thrown by Sudhir \[{{H}_{2}}=\frac{u_{2}^{2}{{\sin }^{2}}({{90}^{o}}-\theta )}{2g}\]\[=\frac{u_{2}^{2}{{\cos }^{2}}\theta }{2g}\] \ \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{u_{1}^{2}/2g}{u_{2}^{2}{{\cos }^{2}}\theta /2g}\] = 1 [As \[{{u}_{1}}={{u}_{2}}\cos \theta \]] Short Trick: Maximum height H µ T2 \[\frac{{{H}_{1}}}{{{H}_{2}}}={{\left( \frac{{{T}_{1}}}{{{T}_{2}}} \right)}^{2}}\]. \ \[\frac{{{H}_{1}}}{{{H}_{2}}}=1\] (As \[{{T}_{1}}={{T}_{2}}\]) Problem 54. A boy aims a gun at a bird from a point, at a horizontal distance of 100 m. If the gun can impart a velocity of \[500 m{{s}^{1}}\] to the bullet. At what height above the bird must he aim his gun in order to hit it (take \[\operatorname{g} = 10 m{{s}^{2}}\]) [CPMT 1996] (a) 20 cm (b) 10 cm (c) 50 cm (d) 100 cm Solution: (a) Time taken by bullet to travel a horizontal distance of 100 m is given by \[t=\frac{100}{500}=\frac{1}{5}sec\] In this time the bullet also moves downward due to gravity its vertical displacement \[h=\frac{1}{2}g\,{{t}^{2}}=\frac{1}{2}\times 10\times {{\left( \frac{1}{5} \right)}^{2}}\]\[=1/5\,m= 20 cm\] So bullet should be fired aiming 20 cm above the bird to hit it. Problem 55. The maximum horizontal range of a projectile is 400 m. The maximum height attained by it will be (a) 100 m (b) 200 m (c) 400 m (d) 800 m Solution: (a) \[{{R}_{\max }}=400\,m\] [when \[\theta =45{}^\circ \]] So from the Relation \[R=4H\cot \theta \Rightarrow 400=4H\cot 45{}^\circ \Rightarrow \,H=100\,m.\] Problem 56. Two bodies are projected with the same velocity. If one is projected at an angle of \[{{30}^{o}}\] and the other at an angle of \[{{60}^{o}}\] to the horizontal, the ratio of the maximum heights reached is [EAMCET (Med.) 1995; Pb. PMT 2000; AIIMS 2001] (a) 3 : 1 (b) 1 : 3 (c) 1 : 2 (d) 2 : 1 Solution: (b) \[\frac{{{H}_{1}}}{{{H}_{2}}}=\frac{{{\sin }^{2}}{{\theta }_{1}}}{{{\sin }^{2}}{{\theta }_{2}}}=\frac{{{\sin }^{2}}{{30}^{o}}}{{{\sin }^{2}}{{60}^{o}}}=\frac{1}{3}\] Problem 57. If time of flight of a projectile is 10 seconds. Range is 500 m. The maximum height attained by it will be [RPMT 1997; RPET 1998] (a) 125 m (b) 50 m (c) 100 m (d) 150 m Solution: (a) \[T=\frac{2u\sin \theta }{g}=10\,\sec \Rightarrow \,u\sin \theta =50\] so \[H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{{{(50)}^{2}}}{2\times 10}=125\,m\]. Problem 58. A man can throw a stone 80 m. The maximum height to which he can raise the stone is (a) 10 m (b) 15 m (c) 30 m (d) 40 m Solution: (d) The problem is different from problem no. (54). In that problem for a given angle of projection range was given and we had find maximum height for that angle. But in this problem angle of projection can vary, \[{{R}_{\max }}=\frac{{{u}^{2}}}{g}=80\,m\] [for \[\theta =45{}^\circ \]] But height can be maximum when body projected vertically up \[{{H}_{\max }}=\frac{{{u}^{2}}{{\sin }^{2}}{{90}^{o}}}{2g}=\frac{{{u}^{2}}}{2g}=\frac{1}{2}\left( \frac{{{u}^{2}}}{g} \right)=40\,m\] Problem 59. A ball is thrown at different angles with the same speed u and from the same points and it has same range in both the cases. If \[{{y}_{1}}and\text{ }{{y}_{2}}\] be the heights attained in the two cases, then \[{{y}_{1}}+{{y}_{2}}=\] (a) \[\frac{{{u}^{2}}}{g}\] (b) \[\frac{2{{u}^{2}}}{g}\] (c) \[\frac{{{u}^{2}}}{2g}\] (d) \[\frac{{{u}^{2}}}{4g}\] Solution (c) Same ranges can be obtained for complementary angles i.e. \[\theta \] and \[{{90}^{o}}\theta \] \[{{y}_{1}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] and \[{{y}_{2}}=\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}\] \[\therefore \,\,\,\,{{y}_{1}}+{{y}_{2}}=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}+\frac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}=\frac{{{u}^{2}}}{2g}\]
You need to login to perform this action.
You will be redirected in
3 sec
