NEET Physics Two Dimensional Motion Circular Motion

Circular Motion Circular motion is another example of motion in two dimensions. To create circular motion in a body it must be given some initial velocity and a force must then act on the body which is always directed at right angles to instantaneous velocity. Since this force is always at right angles to the displacement due to the initial velocity therefore no work is done by the force on the particle. Hence, its kinetic energy and thus speed is unaffected. But due to simultaneous action of the force and the velocity the particle follows resultant path, which in this case is a circle. Circular motion can be classified into two types ? Uniform circular motion and non-uniform circular motion. 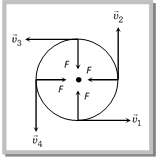Variables of Circular Motion. (1) Displacement and Distance: When particle moves in a circular path describing an angle q during time t (as shown in the figure) from the position A to the position B, we see that the magnitude of the position vector \[\vec{r}\] (that is equal to the radius of the circle) remains constant. i.e., \[\left| {{{\vec{r}}}_{1}} \right|\,=\,\left| {{{\vec{r}}}_{2}} \right|=r\] and the direction of the position vector changes from time to time. (i) Displacement: The change of position vector or the displacement \[\Delta \vec{r}\] of the particle from position A to the position B is given by referring the figure.             \[\Delta \,\vec{r}={{\vec{r}}_{2}}-{{\vec{r}}_{1}}\]             \[\Rightarrow \,\,\Delta r=\,\left| \Delta \vec{r} \right|\,=\,\left| {{{\vec{r}}}_{2}}-{{{\bar{r}}}_{1}} \right|\,\,\,\,\,\Delta r=\,\sqrt{r_{1}^{2}+r_{2}^{2}-2{{r}_{1}}{{r}_{2}}\,\cos \theta }\]  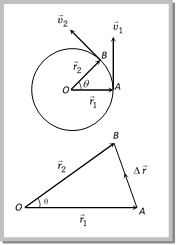                       Putting \[{{r}_{1}}={{r}_{2}}=r\] we obtain             \[\Delta r=\sqrt{{{r}^{2}}+{{r}^{2}}-2r.r\,\cos \theta }\]             \[\Rightarrow \Delta r=\sqrt{2{{r}^{2}}\left( 1-\cos \theta  \right)}\,=\,\sqrt{2{{r}^{2}}\left( 2{{\sin }^{2}}\frac{\theta }{2} \right)}\] \[\Delta \,r=2r\,\sin \frac{\theta }{2}\] (ii) Distance: The distanced covered by the particle during the time t is given as             \[\operatorname{d} = length of the arc AB = r\,\theta \] (iii) Ratio of distance and displacement: \[\frac{d}{\Delta r}=\frac{r\theta }{2r\,\sin \theta /2}=\frac{\theta }{2}\text{cosec}\,(\theta /2)\] Sample problems based on distance and displacement Problem 80. A particle is rotating in a circle of radius r. The distance traversed by it in completing half circle would be              (a) r                  (b) \[\pi r\]                      (c) \[2\pi r\]                    (d) Zero Solution: (b) Distance travelled by particle = Semi-circumference \[=\pi r\]. Problem 81. An athlete completes one round of a circular track of radius 10 m in 40 sec. The distance covered by him in 2 min 20 sec is [Kerala PMT 2002] (a) 70 m            (b) 140 m          (c) 110 m           (d) 220 m Solution: (d) \[\text{No}\text{. of revolution}\,\text{(}n\text{)}=\frac{\text{Total time of mo}\text{tion}}{\text{Time}\,\text{period}}=\frac{140\,\sec }{40\,\sec }=3.5\,\] Distance covered by an athlete in revolution \[=\,\,\,n\,(2\pi \,r)=3.5\,(2\pi \,r)=3.5\times 2\times \frac{22}{7}\times 10=220\,m.\] Problem 82. A wheel covers a distance of 9.5 km in 2000 revolutions. The diameter of the wheel is [RPMT 1999; BHU 2000] (a) 15                (b) 7.5 m           (c) 1.5 m           (d) 7.5 m Solution: (c) Distance \[=n\,(2\pi \,r)\Rightarrow 9.5\times {{10}^{3}}=2000\times (\pi D)\Rightarrow D=\frac{9.5\times {{10}^{3}}}{2000\times \pi }=1.5\,m.\]             (2) Angular displacement (q): The angle turned by a body moving on a circle from some reference line is called angular displacement. (i) Dimension = \[\left[ {{M}^{0}}{{L}^{0}}{{T}^{0}} \right]\] (as \[\theta =arc/\text{radius)}\]. (ii) Units = Radian or Degree. It is sometimes also specified in terms of fraction or multiple of revolution. (iii) \[2\pi \,\text{rad}\,=\,{{360}^{o}}=1\,\text{Revolution}\] (iv) Angular displacement is a axial vector quantity.                             Its direction depends upon the sense of rotation of the object and can be given by Right Hand Rule; which states that if the curvature of the fingers of right hand represents the sense of rotation of the object, then the thumb, held perpendicular to the curvature of the fingers, represents the direction of angular displacement vector.  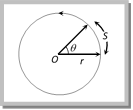           (v) Relation between linear displacement and angular displacement \[\overrightarrow{s}=\overrightarrow{\theta }\times \overrightarrow{r}\] or         \[s=r\theta \] Sample problem based on angular displacement Problem 83. A flywheel rotates at a constant speed of 3000 rpm. The angle described by the shaft in radian in one second is (a) 2 p               (b) 30 p             (c) 100 p            (d) 3000 p Solution: (c) Angular speed \[=3000\,rpm\]\[=50\,rps\] \[=50\times 2\pi \,rad/\sec \]\[=100\pi \,rad/\sec \] i.e. angle described by the shaft in one second is \[100\,\pi \]rad. Problem 84. A particle completes 1.5 revolutions in a circular path of radius 2 cm. The angular displacement of the particle will be ? (in radian) (a) \[6\,\pi \]                   (b) \[3\,\pi \]                   (c) \[2\,\pi \]                   (d) \[\pi \] Solution: (b) 1 revolution mean the angular displacement of \[2\pi \,rad\] \[\therefore 1.5\] revolution means \[1.5\times 2\pi =3\,\pi \,rad\]. (3) Angular velocity (w): Angular velocity of an object in circular motion is defined as the time rate of change of its angular displacement. (i) Angular velocity \[\omega =\frac{\text{angle}\,\text{ traced}}{\text{time}\,\text{ taken}}=\underset{\Delta t\to 0}{\mathop{Lt}}\,\frac{\Delta \theta }{\Delta t}=\frac{d\theta }{dt}\] \[\therefore \,\,\,\,\omega =\frac{d\theta }{dt}\] (ii) Dimension: \[\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]\] (iii) Units: Radians per second \[\left( rad.{{s}^{1}} \right)\] or Degree per second. (iv) Angular velocity is an axial vector. (v) Relation between angular velocity and linear velocity \[\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{\,r}\] Its direction is the same as that of \[\Delta \theta \]. For anticlockwise rotation of the point object on the circular path, the direction of w, according to Right hand rule is along the axis of circular path directed upwards.  For clockwise rotation of the point object on the circular path, the direction of \[\omega \] is along the axis of circular path directed downwards. Note: It is important to note that nothing actually moves in the direction of the angular velocity vector \[\overrightarrow{\omega }\]. The direction of \[\overrightarrow{\omega }\] simply represents that the rotational motion is taking place in a plane perpendicular to it. (vi) For uniform circular motion w remains constant whereas for non-uniform motion w varies with respect to time.   Sample problems based on angular velocity Problem 85. A scooter is going round a circular road of radius 100 m at a speed of 10 m/s.  The angular speed of the scooter will be [Pb. PMT 2002] (a) 0.01 rad/s     (b) 0.1 rad/s       (c) 1 rad/s          (d) 10 rad/s Solution: (b) \[\omega =\frac{v}{r}=\frac{10}{100}=0.1\,rad/sec\] Problem 86. The ratio of angular velocity of rotation of minute hand of a clock with the angular velocity of rotation of the earth about its own axis is (a) 12    (b) 6      (c) 24    (d) None of these Solution: (c) \[{{\omega }_{Minute\,hand}}=\frac{2\pi }{60}\frac{rad}{\min }\] and \[{{\omega }_{Earth}}=\frac{2\pi }{24}\frac{Rad}{hr}=\frac{2\pi }{24\times 60}\frac{rad}{\min }\] \[\therefore \frac{{{\omega }_{Minute\,hand}}}{{{\omega }_{Earth}}}=24:1\] Problem 87. A particle P is moving in a circle of radius ?a? with a uniform speed v. C is the centre of the circle and AB is a diameter. When passing through B the angular velocity of P about A and C are in the ratio [NCERT 1982] (a) 1 : 1             (b) 1 : 2             (c) 2 : 1             (d) 4 : 1 Solution: (b) Angular velocity of P about A \[{{\omega }_{A}}=\frac{v}{2a}\] Angular velocity of P about C 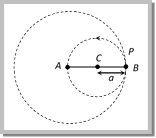\[{{\omega }_{C}}=\frac{v}{a}\] \[\therefore \,\,\,\frac{{{\omega }_{A}}}{{{\omega }_{C}}}=1:2\] Problem 88. The length of the seconds hand of a watch is 10 mm. What is the change in the angular speed of the watch after 15 seconds (a) Zero             (b) \[(10\pi /2)\,\,mm{{s}^{-1}}\]           (c) \[(20/\pi )\,\,mm{{s}^{-1}}\] (d) \[10\sqrt{2}\,\,mm{{s}^{-1}}\] Solution: (a) Angular speed of seconds hand of watch is constant and equal to \[\frac{2\pi }{60}\frac{rad}{sec}\]\[=\frac{\pi }{30}rad/sec\]. So change in angular speed will be zero. (4) Change in velocity: We want to know the magnitude and direction of the change in velocity of the particle which is performing uniform circular motion as it moves from A to B during time t as shown in figure. The change in velocity vector is given as  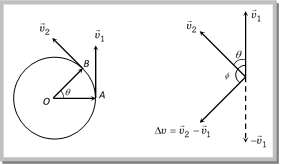                       \[\Delta \vec{v}={{\bar{v}}_{2}}-{{\vec{v}}_{1}}\] or \[\left| \Delta \vec{v} \right|\,=\,\left| {{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}} \right|\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\Delta v\,=\,\sqrt{v_{1}^{2}+v_{2}^{2}-2{{v}_{1}}{{v}_{2}}\cos \theta }\] For uniform circular motion \[{{v}_{1}}={{v}_{2}}=v\] So  \[\Delta v=\sqrt{2{{v}^{2}}\left( 1-\cos \theta  \right)}=2v\,\sin \frac{\theta }{2}\] The direction of \[\Delta \vec{v}\] is shown in figure that can be given as \[\varphi \,=\frac{{{180}^{o}}-\theta }{2}=\left( {{90}^{o}}-\theta /2 \right)\] Note: q Relation between linear velocity and angular velocity.         In vector form \[\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}\] Sample problems based on velocity Problem 89. If a particle moves in a circle describing equal angles in equal times, its velocity vector [CPMT 1972, 74; JIPMER 1997] (a) Remains constant                               (b) Changes in magnitude (c) Changes in direction                            (d) Changes both in magnitude and direction Solution: (c) In uniform circular motion velocity vector changes in direction but its magnitude always remains constant. \[|\overrightarrow{{{v}_{1}}}|\,=\,|\overrightarrow{{{v}_{2}}}|\,=\,|\overrightarrow{{{v}_{3}}}|\,=\,|\overrightarrow{{{v}_{4}}}|\,\,=\,\,cons\tan t\] 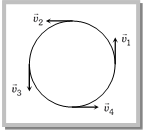Problem 90. A body is whirled in a horizontal circle of radius 20 cm. It has angular velocity of 10 rad/s. What is its linear velocity at any point on circular path [CBSE PMT 1996; JIPMER 2000] (a) 10 m/s          (b) 2 m/s            (c) 20 m/s          (d) \[\sqrt{2}\]m/s Solution: (b) \[v=r\,\omega =0.2\times 10\,=2\,m/s\]             Problem 91. The linear velocity of a point on the equator is nearly (radius of the earth is 6400 km) (a) 800 km/hr     (b) 1600 km/hr   (c) 3200 km/hr    (d) 6400 km/hr Solution: (b) \[v=r\,w=6400\,km\times \frac{2\pi }{24}\frac{rad}{hr}\]\[=1675\,km/hr\]\[=1600\,km/hr\] Problem 92. A particle moves along a circle with a uniform speed v. After it has made an angle of 60o its speed will be [RPMT 1998] (a) \[v\sqrt{2}\]  (b) \[\frac{v}{\sqrt{2}}\]             (c) \[\frac{v}{\sqrt{3}}\]             (d) v Solution: (d) Uniform speed means speed of the particle remains always constant. Problem 93. A particle is moving along a circular path of radius 2 m and with uniform speed of \[5 m{{s}^{1}}\]. What will be the change in velocity when the particle completes half of the revolution  . (a) Zero             (b) \[10 m{{s}^{1}}\]   (c) \[10\sqrt{2}\,m{{s}^{-1}}\]  (d) \[10/\sqrt{2}\,m{{s}^{-1}}\] Solution: (b) \[\Delta v=2v\sin \left( \frac{\theta }{2} \right)=2\times 5\sin \left( \frac{{{180}^{o}}}{2} \right)\]  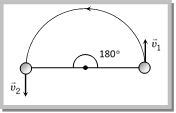            \[=2\times 5\sin {{90}^{o}}=10\,m/s\]             Problem 94. What is the value of linear velocity, if \[\vec{\omega }=3\hat{i}-4\hat{j}+\hat{k}\] and \[\vec{r}=5\hat{i}-6\hat{j}+6\hat{k}\] [Pb. PMT 2000] (a) \[6\hat{i}+2\hat{j}-3\hat{k}\]            (b) \[18\hat{i}+13\hat{j}-2\hat{k}\]         (c) \[4\hat{i}-13\hat{j}+6\hat{k}\]                  (d) \[6\hat{i}-2\hat{j}+8\hat{k}\] Solution: (b) \[\vec{v}=\vec{\omega }\times \vec{r}=\,\left| \,\begin{matrix}    {\hat{i}} & \,\,\,\,\hat{J} & \,\hat{k}  \\    3 & \,\,\,-4\,\,\, & 1  \\    5 & \,\,\,\,-6\,\,\,\, & 6  \\ \end{matrix}\, \right|\] \[\vec{v}=(-24+6)\,i-(18-5)\,\hat{J}+(-18+20)\,\hat{k}=18\,\hat{i}+13\,\hat{J}-2\hat{k}\] Problem 95. A particle comes round circle of radius 1 m once. The time taken by it is 10 sec. The average velocity of motion is [JIPMER 1999] (a) \[0.2\,\,\pi \,m/s\]       (b) \[2\,\,\pi \,\,m/s\]        (c) 2 m/s            (d) Zero Solution: (d) In complete revolution total displacement becomes zero. So the average velocity will be zero. Problem 96. Two particles of mass M and m are moving in a circle of radii R and r. If their time-periods are same, what will be the ratio of their linear velocities [CBSE PMT 2001] (a) MR : mr        (b) M : m           (c) R : r              (d) 1 : 1 Solution: (c) \[\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{{{r}_{1}}{{\omega }_{1}}}{{{r}_{2}}{{\omega }_{2}}}\]. Time periods are equal i.e. \[{{\omega }_{1}}={{\omega }_{2}}\therefore \,\,\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{R}{r}\] (5) Time period (T): In circular motion, the time period is defined as the time taken by the object to complete one revolution on its circular path. (i) Units: second. (ii) Dimension: \[\left[ {{M}^{0}}{{L}^{0}}T \right]\] (iii) Time period of second?s hand of watch = 60 second. (iv) Time period of minute?s hand of watch = 60 minute (v) Time period of hour?s hand of watch = 12 hour (6) Frequency (n): In circular motion, the frequency is defined as the number of revolutions completed by the object on its circular path in a unit time. (i) Units: s?1 or hertz (Hz). (ii) Dimension: \[\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]\]             · Note:  Relation between time period and frequency: If n is the frequency of revolution of an object in circular motion, then the object completes n revolutions in 1 second. Therefore, the object will complete one revolution in 1/n second. \[\therefore \,\,\,\,T=1/n\] · Relation between angular velocity, frequency and time period: Consider a point object describing a uniform circular motion with frequency n and time period T. When the object completes one revolution, the angle traced at its axis of circular motion is \[2\pi \] radians. It means, when time t = T, \[\theta =2\pi \] radians. Hence, angular velocity \[\omega =\frac{\theta }{t}=\frac{2\pi }{T}=2\pi n\]         \[\left( \because \,\,\,\operatorname{T} = 1/n \right)\] \[\omega =\frac{2\pi }{T}=2\pi n\] · If two particles are moving on same circle or different coplanar concentric circles in same direction with different uniform angular speeds \[{{\omega }_{A}}\,and\,\,{{\omega }_{B}}\] respectively, the angular velocity of B relative to A will be \[{{\omega }_{\text{rel}}}={{\omega }_{B}}-{{\omega }_{A}}\] So the time taken by one to complete one revolution around O with respect to the other (i.e., time in which B complete one revolution around O with respect to the other (i.e., time in which B completes one more or less revolution around O than A) \[T=\frac{2\pi }{{{\omega }_{\text{rel}}}}=\frac{2\pi }{{{\omega }_{2}}-{{\omega }_{1}}}=\frac{{{T}_{1}}{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\]             \[\left[ \text{as }T=\frac{2\pi }{\omega } \right]\] Special case: If \[{{\omega }_{B}}={{\omega }_{A}},\,{{\omega }_{\text{rel}}}=0\] and so \[T=\infty \]., particles will maintain their position relative to each other. This is what actually happens in case of geostationary satellite \[({{\omega }_{1}}={{\omega }_{2}}= constant)\]                         (7) Angular acceleration (a): Angular acceleration of an object in circular motion is defined as the time rate of change of its angular velocity. (i) If \[\Delta \omega \] be the change in angular velocity of the object in time interval t and \[t+\Delta t\], while moving on a circular path, then angular acceleration of the object will be             \[\alpha =\underset{\Delta t\to 0}{\mathop{Lt}}\,\,\frac{\Delta \omega }{\Delta t}=\frac{d\omega }{dt}\,=\frac{{{d}^{2}}\theta }{d{{t}^{2}}}\] (ii) Units: \[\operatorname{rad}. {{s}^{2}}\] (iii) Dimension: \[\left[ {{M}^{0}}{{L}^{0}}{{T}^{2}} \right]\] (iv) Relation between linear acceleration and angular acceleration \[\overrightarrow{a}=\overrightarrow{\alpha }\times \overrightarrow{r}\]         (v) For uniform circular motion since \[\omega \] is constant so \[\alpha =\frac{d\omega }{dt}=0\] (vi) For non-uniform circular motion \[\alpha \ne 0\]                         · Note:  Relation between linear (tangential) acceleration and angular acceleration \[\overrightarrow{a}=\overrightarrow{\alpha }\times \overrightarrow{r}\] · For uniform circular motion angular acceleration is zero, so tangential acceleration also is equal to zero. · For non-uniform circular motion \[\operatorname{a}\ne 0\] (because \[\operatorname{a}\ne 0\]).         Sample problems based on angular acceleration Problem 97. A body is revolving with a uniform speed v in a circle of radius r. The angular acceleration of the body is (a) \[\frac{v}{r}\]                                                                       (b) Zero (c) \[\frac{{{v}^{2}}}{r}\] along the radius and towards the centre (d) \[\frac{{{v}^{2}}}{r}\] along the radius and away from the centre Solution: (b) In uniform circular motion \[\omega \] constant so \[\alpha =\frac{d\omega }{dt}=0\] Problem 98. The linear acceleration of a car is \[10m/{{s}^{2}}\]. If the wheels of the car have a diameter of 1 m, the angular acceleration of the wheels will be (a) \[10 rad/se{{c}^{2}}\]                      (b) \[20\text{ }rad/se{{c}^{2}}\]            (c) \[1\text{ }rad/se{{c}^{2}}\]                   (d) \[2\text{ }rad/se{{c}^{2}}\] Solution: (b) \[\text{Angular acceleration}=\frac{\text{linear acceleration}}{\text{radius}}=\frac{10}{0.5}=20\,rad/se{{c}^{2}}\]             Problem 99. The angular speed of a motor increases from 600 rpm to 1200 rpm in 10 s. What is the angular acceleration of the motor. (a) \[600\,\,rad\,se{{c}^{-2}}\]   (b) \[60\pi \,rad\,se{{c}^{-2}}\]  (c) \[60\,rad\,se{{c}^{-2}}\]                   (d) \[2\pi \,rad\,se{{c}^{-2}}\] Solution: (d) \[\alpha =\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}=\frac{2\pi ({{n}_{2}}-{{n}_{1}})}{t}=\frac{2\pi (1200-600)}{10\times 60}\frac{rad}{se{{c}^{2}}}=2\pi \,rad/se{{c}^{2}}\]