Motion in Vertical Circle
Category : NEET
Motion in Vertical Circle This is an example of non-uniform circular motion. In this motion body is under the influence of gravity of earth. When body moves from lowest point to highest point. Its speed decrease and becomes minimum at highest point. Total mechanical energy of the body remains conserved and KE converts into PE and vice versa. (1) Velocity at any point on vertical loop: If u is the initial velocity imparted to body at lowest point then. Velocity of body at height h is given by 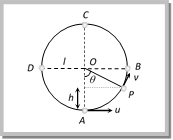 \[v=\sqrt{{{u}^{2}}-2gh}=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\] \[[As h = l l cos\,\theta = l (1 cos\,\theta )]\] where l in the length of the string (2) Tension at any point on vertical loop: Tension at general point P, According to Newton?s second law of motion. Net force towards centre = centripetal force \[T-mg\cos \theta =\frac{m{{v}^{2}}}{l}\] or \[T=mg\cos \theta +\frac{m{{v}^{2}}}{l}\] \[T=\frac{m}{l}[{{u}^{2}}-gl(2-3\cos \theta )]\] [As \[v=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\]
\[v=\sqrt{{{u}^{2}}-2gh}=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\] \[[As h = l l cos\,\theta = l (1 cos\,\theta )]\] where l in the length of the string (2) Tension at any point on vertical loop: Tension at general point P, According to Newton?s second law of motion. Net force towards centre = centripetal force \[T-mg\cos \theta =\frac{m{{v}^{2}}}{l}\] or \[T=mg\cos \theta +\frac{m{{v}^{2}}}{l}\] \[T=\frac{m}{l}[{{u}^{2}}-gl(2-3\cos \theta )]\] [As \[v=\sqrt{{{u}^{2}}-2gl(1-\cos \theta )}\]  (3) Velocity and tension in a vertical loop at different positions
(3) Velocity and tension in a vertical loop at different positions
| Position | Angle | Velocity | Tension |
| A | 0o | u | \[\frac{m{{u}^{2}}}{l}+mg\] |
| B | 90o | \[\sqrt{{{u}^{2}}-2gl}\] | \[\frac{m{{u}^{2}}}{l}-2mg\] |
| C | 180o | \[\sqrt{{{u}^{2}}-4gl}\] | \[\frac{m{{u}^{2}}}{l}-5mg\] |
| D | 270o | \[\sqrt{{{u}^{2}}-2gl}\] | \[\frac{m{{u}^{2}}}{l}-2mg\] |
| Velocity at lowest point | Condition |
| \[{{u}_{A}}>\sqrt{5gl}\] | Tension in the string will not be zero at any of the point and body will continue the circular motion. |
| \[{{u}_{A}}=\sqrt{5gl},\] | Tension at highest point C will be zero and body will just complete the circle. |
| \[\sqrt{2gl}<{{u}_{A}}<\sqrt{5gl},\] | Particle will not follow circular motion. Tension in string become zero somewhere between points B and C whereas velocity remain positive. Particle leaves circular path and follow parabolic trajectory. |
| \[{{u}_{A}}=\sqrt{2gl}\] | Both velocity and tension in the string becomes zero between A and B and particle will oscillate along semi-circular path. |
| \[{{u}_{A}}<\sqrt{2gl}\] | velocity of particle becomes zero between A and B but tension will not be zero and the particle will oscillate about the point A. |
| Quantity | Point A | Point B | Point C | Point D | Point P |
| Linear velocity (v) | \[\sqrt{5gl}\] | \[\sqrt{3gl}\] | \[\sqrt{gl}\] | \[\sqrt{3gl}\] | \[\sqrt{gl\,(3+2\cos \theta )}\] |
| Angular velocity (w) | \[\sqrt{\frac{5g}{l}}\] | \[\sqrt{\frac{3g}{l}}\] | \[\sqrt{\frac{g}{l}}\] | \[\sqrt{\frac{3g}{l}}\] | \[\sqrt{\frac{g}{l}\,(3+2\cos \theta )}\] |
| Tension in String (T) | 6 mg | 3 mg | 0 | 3 mg | \[3mg\,(1+\cos \theta )\] |
| Kinetic Energy (KE) | \[\frac{5}{2}mgl\] | \[\frac{3}{2}mgl\] | \[\frac{1}{2}mgl\] | \[\frac{3}{2}mgl\] | \[\frac{m{{u}^{2}}}{l}-5mg=0\] |
| Potential Energy (PE) | 0 | mgl | 2 mgl | mgl | \[mgl\,(1-\cos \theta )\] |
| Total Energy (TE) | \[\frac{5}{2}mgl\] | \[\frac{5}{2}mgl\] | \[\frac{5}{2}mgl\] | \[\frac{5}{2}mgl\] | \[\frac{5}{2}mgl\] |
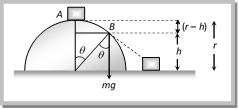 For point A and B, by law of conservation of energy Total energy at point A = Total energy at point B \[\operatorname{K}.E{{.}_{(A)}}+ P.E{{.}_{(A)}}= K.E{{.}_{(B)}}+ P.E{{.}_{(B)}}\] \[0+mgr=\frac{1}{2}m{{v}^{2}}+mgh\Rightarrow v=\sqrt{2g(r-h)}\] ..... (ii) and from the given figure \[h=r\cos \theta \] .....(iii) By substituting the value of v and h from \[e{{q}^{n}}\] (ii) and (iii) in \[e{{q}^{n}}\] (i) \[mg\,\left( \frac{h}{r} \right)=\frac{m}{r}{{\left( \sqrt{2g\,(r-h)}\, \right)}^{2}}\] \[\Rightarrow h=2\,(r-h)\Rightarrow h=\frac{2}{3}r\] i.e. the block lose contact at the height of \[\frac{2}{3}r\] from the ground. and angle from the vertical can be given by \[\cos \theta =\frac{h}{r}=\frac{2}{3}\] \[\therefore \,\,\,\theta ={{\cos }^{-1}}\frac{2}{3}\]. Sample problems based on vertical looping Problem 156. A small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in [IIT-JEE (Screening) 2001] (a)
For point A and B, by law of conservation of energy Total energy at point A = Total energy at point B \[\operatorname{K}.E{{.}_{(A)}}+ P.E{{.}_{(A)}}= K.E{{.}_{(B)}}+ P.E{{.}_{(B)}}\] \[0+mgr=\frac{1}{2}m{{v}^{2}}+mgh\Rightarrow v=\sqrt{2g(r-h)}\] ..... (ii) and from the given figure \[h=r\cos \theta \] .....(iii) By substituting the value of v and h from \[e{{q}^{n}}\] (ii) and (iii) in \[e{{q}^{n}}\] (i) \[mg\,\left( \frac{h}{r} \right)=\frac{m}{r}{{\left( \sqrt{2g\,(r-h)}\, \right)}^{2}}\] \[\Rightarrow h=2\,(r-h)\Rightarrow h=\frac{2}{3}r\] i.e. the block lose contact at the height of \[\frac{2}{3}r\] from the ground. and angle from the vertical can be given by \[\cos \theta =\frac{h}{r}=\frac{2}{3}\] \[\therefore \,\,\,\theta ={{\cos }^{-1}}\frac{2}{3}\]. Sample problems based on vertical looping Problem 156. A small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in [IIT-JEE (Screening) 2001] (a)  (b)
(b)  (c)
(c)  (d)
(d)  Solution: (a) Normal reaction at the highest point of the path \[R=\frac{m{{v}^{2}}}{r}-mg\] For maximum R, value of the radius of curvature (r) should be minimum and it is minimum in first condition. Problem 157. A stone tied to string is rotated in a vertical circle. The minimum speed with which the string has to be rotated [EAMCET (Engg.) 1998; CBSE PMT 1999] (a) Decreases with increasing mass of the stone (b) Is independent of the mass of the stone (c) Decreases with increasing in length of the string (d) Is independent of the length of the string Solution: (b) \[v=\sqrt{5g\,r}\] for lowest point of vertical loop. \[v\propto {{m}^{0}}\] i.e. it does not depends on the mass of the body. Problem 158. A mass m is revolving in a vertical circle at the end of a string of length 20 cms. By how much does the tension of the string at the lowest point exceed the tension at the topmost point (a) 2 mg (b) 4 mg (c) 6 mg (d) 8 mg Solution: (c) \[{{T}_{\text{Lowest}\,\text{point}}}-{{T}_{\text{Highest}\,\text{point}}}=6\,mg\] (Always) Problem 159. In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle \[\theta \] with the vertical (a) \[\theta \ =\ {{\cos }^{-1}}(1/3)\] (b) \[\theta ={{60}^{o}}\] (c) \[\theta \ =\ {{\cos }^{-1}}(2/3)\] (d) \[\theta \ =\ {{0}^{o}}\] Solution: (c) Let the string breaks at point B. Tension \[=\,\,mg\cos \theta +\frac{m\,v_{B}^{2}}{r}=\] Breaking strength \[=mg\cos \theta +\frac{m\,v_{B}^{2}}{r}=2\,mg\] ?. (i) If the bob is released from rest (from point A) then velocity acquired by it at point B \[{{v}_{B}}=\sqrt{2gh}\]
Solution: (a) Normal reaction at the highest point of the path \[R=\frac{m{{v}^{2}}}{r}-mg\] For maximum R, value of the radius of curvature (r) should be minimum and it is minimum in first condition. Problem 157. A stone tied to string is rotated in a vertical circle. The minimum speed with which the string has to be rotated [EAMCET (Engg.) 1998; CBSE PMT 1999] (a) Decreases with increasing mass of the stone (b) Is independent of the mass of the stone (c) Decreases with increasing in length of the string (d) Is independent of the length of the string Solution: (b) \[v=\sqrt{5g\,r}\] for lowest point of vertical loop. \[v\propto {{m}^{0}}\] i.e. it does not depends on the mass of the body. Problem 158. A mass m is revolving in a vertical circle at the end of a string of length 20 cms. By how much does the tension of the string at the lowest point exceed the tension at the topmost point (a) 2 mg (b) 4 mg (c) 6 mg (d) 8 mg Solution: (c) \[{{T}_{\text{Lowest}\,\text{point}}}-{{T}_{\text{Highest}\,\text{point}}}=6\,mg\] (Always) Problem 159. In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle \[\theta \] with the vertical (a) \[\theta \ =\ {{\cos }^{-1}}(1/3)\] (b) \[\theta ={{60}^{o}}\] (c) \[\theta \ =\ {{\cos }^{-1}}(2/3)\] (d) \[\theta \ =\ {{0}^{o}}\] Solution: (c) Let the string breaks at point B. Tension \[=\,\,mg\cos \theta +\frac{m\,v_{B}^{2}}{r}=\] Breaking strength \[=mg\cos \theta +\frac{m\,v_{B}^{2}}{r}=2\,mg\] ?. (i) If the bob is released from rest (from point A) then velocity acquired by it at point B \[{{v}_{B}}=\sqrt{2gh}\] 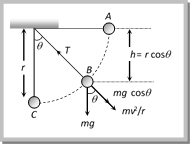 \[{{v}_{B}}=\sqrt{2g\,r\cos \theta }\] .... (ii) \[[As h= r cos\,\,\theta ]\] By substituting this value in equation (i) \[mg\cos \theta +\frac{m}{r}(2g\,r\,\cos \theta )=2\,mg\] or \[3mg\cos \theta =2\,mg\Rightarrow \cos \theta =\frac{2}{3}\] \[\therefore \,\,\theta ={{\cos }^{-1}}\left( \frac{2}{3} \right)\] Problem 160. A toy car rolls down the inclined plane as shown in the fig. It goes around the loop at the bottom. What is the relation between \[H\] and \[h\]
\[{{v}_{B}}=\sqrt{2g\,r\cos \theta }\] .... (ii) \[[As h= r cos\,\,\theta ]\] By substituting this value in equation (i) \[mg\cos \theta +\frac{m}{r}(2g\,r\,\cos \theta )=2\,mg\] or \[3mg\cos \theta =2\,mg\Rightarrow \cos \theta =\frac{2}{3}\] \[\therefore \,\,\theta ={{\cos }^{-1}}\left( \frac{2}{3} \right)\] Problem 160. A toy car rolls down the inclined plane as shown in the fig. It goes around the loop at the bottom. What is the relation between \[H\] and \[h\] 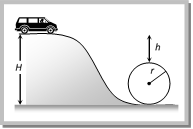 (a) \[\frac{H}{h}=2\] (b) \[\frac{H}{h}=3\] (c) \[\frac{H}{h}=4\] (d) \[\frac{H}{h}=5\] Solution: (d) When car rolls down the inclined plane from height H, then velocity acquired by it at the lowest point \[v=\sqrt{2g\,H}\] ?. (i) and for looping of loop, velocity at the lowest point should be \[v=\sqrt{5g\,r}\] ?. (ii) From \[e{{q}^{n}}\] (i) and (ii) \[v=\sqrt{2gH}=\sqrt{5gr}\] \[\therefore \,\,\,H=\frac{5r}{2}\] ?. (iii) From the figure \[H=h+2r\,\Rightarrow r=\frac{H-h}{2}\] Substituting the value of r in equation (iii) we get \[H=\frac{5}{2}\left[ \frac{H-h}{2} \right]\Rightarrow \frac{H}{h}=5\] Problem 161. The mass of the bob of a simple pendulum of length \[L\] is \[m\]. If the bob is left from its horizontal position then the speed of the bob and the tension in the thread in the lowest position of the bob will be respectively. (a) \[\sqrt{2gL}\,and\,\,3mg\] (b) \[3mg\,\,and\,\,\sqrt{2gL}\] (c) \[2mg\,\,and\,\,\sqrt{2gl}\] (d) \[2gl\,\,and\,\,3mg\]
(a) \[\frac{H}{h}=2\] (b) \[\frac{H}{h}=3\] (c) \[\frac{H}{h}=4\] (d) \[\frac{H}{h}=5\] Solution: (d) When car rolls down the inclined plane from height H, then velocity acquired by it at the lowest point \[v=\sqrt{2g\,H}\] ?. (i) and for looping of loop, velocity at the lowest point should be \[v=\sqrt{5g\,r}\] ?. (ii) From \[e{{q}^{n}}\] (i) and (ii) \[v=\sqrt{2gH}=\sqrt{5gr}\] \[\therefore \,\,\,H=\frac{5r}{2}\] ?. (iii) From the figure \[H=h+2r\,\Rightarrow r=\frac{H-h}{2}\] Substituting the value of r in equation (iii) we get \[H=\frac{5}{2}\left[ \frac{H-h}{2} \right]\Rightarrow \frac{H}{h}=5\] Problem 161. The mass of the bob of a simple pendulum of length \[L\] is \[m\]. If the bob is left from its horizontal position then the speed of the bob and the tension in the thread in the lowest position of the bob will be respectively. (a) \[\sqrt{2gL}\,and\,\,3mg\] (b) \[3mg\,\,and\,\,\sqrt{2gL}\] (c) \[2mg\,\,and\,\,\sqrt{2gl}\] (d) \[2gl\,\,and\,\,3mg\] 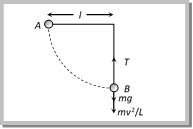 Solution: (a) By the conservation of energy Potential energy at point A = Kinetic energy at point B \[mg\,l=\frac{1}{2}m\,{{v}^{2}}\Rightarrow v=\sqrt{2\,gl}\] and tension \[=mg+\frac{m{{v}^{2}}}{l}\Rightarrow T=mg+\frac{m}{l}(2gl)\Rightarrow T=3\,\,mg\] Problem 162. A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolutions per minute. The total tension in the string when the stone is at its lowest point is [Kerala (Engg.) 2001] (a) \[m\,\{g+({{\pi }^{2}}{{n}^{2}}r)/900\}\] (b) \[m\,(g+\pi \,n{{r}^{2}})\] (c) \[m\,(g+\pi \,nr)\] (d) \[m\,(g+{{n}^{2}}{{r}^{2}})\] Solution: (a) Tension at lowest point \[T=mg+m\,{{w}^{2}}r=mg+m4{{\pi }^{2}}{{n}^{2}}r\] If n is revolution per minute then \[T=mg+m4{{\pi }^{2}}\frac{{{n}^{2}}}{3600}r=mg+\frac{m{{\pi }^{2}}{{n}^{2}}r}{900}=m\left[ g+\frac{{{\pi }^{2}}{{n}^{2}}r}{900} \right]\] Problem 163. A particle is kept at rest at the top of a sphere of diameter 42m. When disturbed slightly, it slides down. At what height \[h\] from the bottom, the particle will leave the sphere [IMS-BHU 2003] (a) 14 m (b) 28 m (c) 35 m (d) 7 m Solution: (c) Let the particle leave the sphere at height ?h? from the bottom
Solution: (a) By the conservation of energy Potential energy at point A = Kinetic energy at point B \[mg\,l=\frac{1}{2}m\,{{v}^{2}}\Rightarrow v=\sqrt{2\,gl}\] and tension \[=mg+\frac{m{{v}^{2}}}{l}\Rightarrow T=mg+\frac{m}{l}(2gl)\Rightarrow T=3\,\,mg\] Problem 162. A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolutions per minute. The total tension in the string when the stone is at its lowest point is [Kerala (Engg.) 2001] (a) \[m\,\{g+({{\pi }^{2}}{{n}^{2}}r)/900\}\] (b) \[m\,(g+\pi \,n{{r}^{2}})\] (c) \[m\,(g+\pi \,nr)\] (d) \[m\,(g+{{n}^{2}}{{r}^{2}})\] Solution: (a) Tension at lowest point \[T=mg+m\,{{w}^{2}}r=mg+m4{{\pi }^{2}}{{n}^{2}}r\] If n is revolution per minute then \[T=mg+m4{{\pi }^{2}}\frac{{{n}^{2}}}{3600}r=mg+\frac{m{{\pi }^{2}}{{n}^{2}}r}{900}=m\left[ g+\frac{{{\pi }^{2}}{{n}^{2}}r}{900} \right]\] Problem 163. A particle is kept at rest at the top of a sphere of diameter 42m. When disturbed slightly, it slides down. At what height \[h\] from the bottom, the particle will leave the sphere [IMS-BHU 2003] (a) 14 m (b) 28 m (c) 35 m (d) 7 m Solution: (c) Let the particle leave the sphere at height ?h? from the bottom 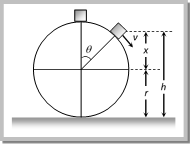 We know for given condition \[x=\frac{2}{3}\,r\] and \[h=r+x\,\,=r+\frac{2}{3}\,r=\frac{5}{3}\,r=\frac{5}{3}\times 21=35\,m\] [As r= 21 m] Problem 164. A bucket tied at the end of a 1.6 m long string is whirled in a vertical circle with constant speed. What should be the minimum speed so that the water from the bucket does not spill, when the bucket is at the highest position (Take \[\operatorname{g} = 10 m/se{{c}^{2}}\]) [AIIMS 1987] (a) \[4\,m/\sec \] (b) \[6.25\,m/sec\] (c) \[16m/sec\] (d) None of these Solution: (a) \[v=\sqrt{g\ r}\,\,=\sqrt{10\times 1.6}\,\,=\sqrt{16}\,\,=4\,m/s\] Problem 165. The ratio of velocities at points A, B and C in vertical circular motion is
We know for given condition \[x=\frac{2}{3}\,r\] and \[h=r+x\,\,=r+\frac{2}{3}\,r=\frac{5}{3}\,r=\frac{5}{3}\times 21=35\,m\] [As r= 21 m] Problem 164. A bucket tied at the end of a 1.6 m long string is whirled in a vertical circle with constant speed. What should be the minimum speed so that the water from the bucket does not spill, when the bucket is at the highest position (Take \[\operatorname{g} = 10 m/se{{c}^{2}}\]) [AIIMS 1987] (a) \[4\,m/\sec \] (b) \[6.25\,m/sec\] (c) \[16m/sec\] (d) None of these Solution: (a) \[v=\sqrt{g\ r}\,\,=\sqrt{10\times 1.6}\,\,=\sqrt{16}\,\,=4\,m/s\] Problem 165. The ratio of velocities at points A, B and C in vertical circular motion is 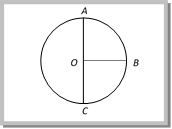 (a) \[1:9:25\] (b) \[1:2:3\] (c) \[1:3:5\] (d) \[1:\sqrt{3}:\sqrt{5}\] Solution: (d) \[{{v}_{A}}:{{v}_{B}}:{{v}_{c}}=\sqrt{g\,r}:\sqrt{3\,g\,r}:\sqrt{5g\,r}=1:\sqrt{3}:\sqrt{5}\] Problem 166. The minimum speed for a particle at the lowest point of a vertical circle of radius R, to describe the circle is ?v?. If the radius of the circle is reduced to one-fourth its value, the corresponding minimum speed will be [EAMCET (Engg.) 1999] (a) \[\frac{v}{4}\] (b) \[\frac{v}{2}\] (c) 2v (d) 4v Solution: (b) \[v=\sqrt{5g\,r}\] \[\therefore \,\,v\propto \sqrt{r}\] So \[\frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{{{r}_{2}}}{{{r}_{1}}}}=\sqrt{\frac{r/4}{r}}=\frac{1}{2}\Rightarrow {{v}_{2}}=v/2\] Problem 167. A body slides down a frictionless track which ends in a circular loop of diameter D, then the minimum height h of the body in term of D so that it may just complete the loop, is [AIIMS 2000] (a) \[h=\frac{5D}{2}\] (b) \[h=\frac{5D}{4}\] (c) \[h=\frac{3D}{4}\] (d) \[h=\frac{D}{4}\] Solution: (b) We know \[h=\frac{5}{2}r=\frac{5}{2}\left( \frac{D}{2} \right)=\frac{5D}{4}\] [For critical condition of vertical looping] Problem 168. A can filled with water is revolved in a vertical circle of radius 4m and the water just does not fall down. The time period of revolution will be [CPMT 1985; RPET 1999] (a) 1 sec (b) 10 sec (c) 8 sec (d) 4 sec Solution: (d) At highest point \[mg=m{{\omega }^{2}}r\Rightarrow g=\frac{4{{\pi }^{2}}}{{{T}^{2}}}\,r\Rightarrow 10=\frac{4{{\pi }^{2}}4}{{{T}^{2}}}\Rightarrow {{T}^{2}}=16\,\,\,\,\,\therefore T=4\,sec\] Problem 169. A particle is moving in a vertical circle. The tensions in the string when passing through two positions at angles \[3{{0}^{o}}\,and 6{{0}^{o}}\] from vertical (lowest position) are \[{{\operatorname{T}}_{1}}\,\,and {{T}_{2}}\] respectively, Then [Orissa JEE 2002] (a) \[{{T}_{1}}={{T}_{2}}\] (b) \[{{T}_{1}}>{{T}_{2}}\] (c) \[{{T}_{1}}<{{T}_{2}}\] (d) \[{{T}_{1}}\ge {{T}_{2}}\] Solution: (b) \[T=mg\cos \theta +\frac{m{{v}^{2}}}{r}\]
(a) \[1:9:25\] (b) \[1:2:3\] (c) \[1:3:5\] (d) \[1:\sqrt{3}:\sqrt{5}\] Solution: (d) \[{{v}_{A}}:{{v}_{B}}:{{v}_{c}}=\sqrt{g\,r}:\sqrt{3\,g\,r}:\sqrt{5g\,r}=1:\sqrt{3}:\sqrt{5}\] Problem 166. The minimum speed for a particle at the lowest point of a vertical circle of radius R, to describe the circle is ?v?. If the radius of the circle is reduced to one-fourth its value, the corresponding minimum speed will be [EAMCET (Engg.) 1999] (a) \[\frac{v}{4}\] (b) \[\frac{v}{2}\] (c) 2v (d) 4v Solution: (b) \[v=\sqrt{5g\,r}\] \[\therefore \,\,v\propto \sqrt{r}\] So \[\frac{{{v}_{2}}}{{{v}_{1}}}=\sqrt{\frac{{{r}_{2}}}{{{r}_{1}}}}=\sqrt{\frac{r/4}{r}}=\frac{1}{2}\Rightarrow {{v}_{2}}=v/2\] Problem 167. A body slides down a frictionless track which ends in a circular loop of diameter D, then the minimum height h of the body in term of D so that it may just complete the loop, is [AIIMS 2000] (a) \[h=\frac{5D}{2}\] (b) \[h=\frac{5D}{4}\] (c) \[h=\frac{3D}{4}\] (d) \[h=\frac{D}{4}\] Solution: (b) We know \[h=\frac{5}{2}r=\frac{5}{2}\left( \frac{D}{2} \right)=\frac{5D}{4}\] [For critical condition of vertical looping] Problem 168. A can filled with water is revolved in a vertical circle of radius 4m and the water just does not fall down. The time period of revolution will be [CPMT 1985; RPET 1999] (a) 1 sec (b) 10 sec (c) 8 sec (d) 4 sec Solution: (d) At highest point \[mg=m{{\omega }^{2}}r\Rightarrow g=\frac{4{{\pi }^{2}}}{{{T}^{2}}}\,r\Rightarrow 10=\frac{4{{\pi }^{2}}4}{{{T}^{2}}}\Rightarrow {{T}^{2}}=16\,\,\,\,\,\therefore T=4\,sec\] Problem 169. A particle is moving in a vertical circle. The tensions in the string when passing through two positions at angles \[3{{0}^{o}}\,and 6{{0}^{o}}\] from vertical (lowest position) are \[{{\operatorname{T}}_{1}}\,\,and {{T}_{2}}\] respectively, Then [Orissa JEE 2002] (a) \[{{T}_{1}}={{T}_{2}}\] (b) \[{{T}_{1}}>{{T}_{2}}\] (c) \[{{T}_{1}}<{{T}_{2}}\] (d) \[{{T}_{1}}\ge {{T}_{2}}\] Solution: (b) \[T=mg\cos \theta +\frac{m{{v}^{2}}}{r}\] 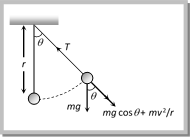 As \[\theta \] increases T decreases So \[{{T}_{1}}>{{T}_{2}}\] Problem 170. A mass of \[2kg\] is tied to the end of a string of length 1m. It is, then, whirled in a vertical circle with a constant speed of \[5\ m{{s}^{-1}}\]. Given that \[g=10\ m{{s}^{-2}}\]. At which of the following locations of tension in the string will be \[70\ N\]. (a) At the top (b) At the bottom (c) When the string is horizontal (d) At none of the above locations Solution: (b) Centrifugal force \[F=\frac{m{{v}^{2}}}{r}=\frac{2\times {{(5)}^{2}}}{1}=50\,Newton\]
As \[\theta \] increases T decreases So \[{{T}_{1}}>{{T}_{2}}\] Problem 170. A mass of \[2kg\] is tied to the end of a string of length 1m. It is, then, whirled in a vertical circle with a constant speed of \[5\ m{{s}^{-1}}\]. Given that \[g=10\ m{{s}^{-2}}\]. At which of the following locations of tension in the string will be \[70\ N\]. (a) At the top (b) At the bottom (c) When the string is horizontal (d) At none of the above locations Solution: (b) Centrifugal force \[F=\frac{m{{v}^{2}}}{r}=\frac{2\times {{(5)}^{2}}}{1}=50\,Newton\] 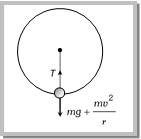 \[Weight=mg=2\times 10=20\,Newton\] Tension = 70 N (sum of above two forces) i.e. the mass is at the bottom of the vertical circular path Problem 171. With what angular velocity should a 20 m long cord be rotated such that tension in it, while reaching the highest point, is zero [RPMT 1999] (a) 0.5 rad/sec (b) 0.2 rad/sec (c) 7.5 rad/sec (d) 0.7 rad/sec Solution: (d) \[\omega =\sqrt{\frac{g}{r}}=\sqrt{\frac{10}{20}}\,\,=\sqrt{0.5}=0.7\,rad/sec\] Problem 172. A body of mass of \[100g\] is attached to a \[1m\] long string and it is revolving in a vertical circle. When the string makes an angle of \[{{60}^{o}}\] with the vertical then its speed is \[2\ m/s\]. The tension in the string at \[\theta ={{60}^{o}}\] will be (a) \[89\ N\] (b) \[0.89\ N\] (c) \[8.9\ N\] (d) \[0.089\ N\] Solution: (b) \[T=mg\cos \theta +\frac{m{{v}^{2}}}{r}\]\[=0.1\times 9.8\times \cos 60+\frac{0.1\times {{(2)}^{2}}}{1}\]\[=0.49+0.4\]\[=0.89\,Newton\] Problem 173. A body of mass \[2kg\] is moving in a vertical circle of radius \[2m\]. The work done when it moves from the lowest point to the highest point is (a) \[80\ J\] (b) \[40\ J\] (c) \[20\ J\] (d) 0 Solution: (a) work done = change in potential energy \[=2\,mgr\]\[=2\times 2\times 10\times 2\]\[=80\,J\] Problem 174. A body of mass \[m\] is tied to one end of a string of length \[l\] and revolves vertically in a circular path. At the lowest point of circle, what must be the K.E. of the body so as to complete the circle [RPMT 1996] (a) \[5\ mgl\] (b) \[4\ mgl\] (c) \[2.5\ mgl\] (d) \[2\ mgl\] Solution: (c) Minimum velocity at lowest point to complete vertical loop \[=\sqrt{5\,gl}\] So minimum kinetic energy \[=\frac{1}{2}m\,({{v}^{2}})\] \[=\frac{1}{2}m\,{{(\sqrt{5gl})}^{2}}\]\[=\frac{5}{2}mgl\]\[=2.5\,mgl\]
\[Weight=mg=2\times 10=20\,Newton\] Tension = 70 N (sum of above two forces) i.e. the mass is at the bottom of the vertical circular path Problem 171. With what angular velocity should a 20 m long cord be rotated such that tension in it, while reaching the highest point, is zero [RPMT 1999] (a) 0.5 rad/sec (b) 0.2 rad/sec (c) 7.5 rad/sec (d) 0.7 rad/sec Solution: (d) \[\omega =\sqrt{\frac{g}{r}}=\sqrt{\frac{10}{20}}\,\,=\sqrt{0.5}=0.7\,rad/sec\] Problem 172. A body of mass of \[100g\] is attached to a \[1m\] long string and it is revolving in a vertical circle. When the string makes an angle of \[{{60}^{o}}\] with the vertical then its speed is \[2\ m/s\]. The tension in the string at \[\theta ={{60}^{o}}\] will be (a) \[89\ N\] (b) \[0.89\ N\] (c) \[8.9\ N\] (d) \[0.089\ N\] Solution: (b) \[T=mg\cos \theta +\frac{m{{v}^{2}}}{r}\]\[=0.1\times 9.8\times \cos 60+\frac{0.1\times {{(2)}^{2}}}{1}\]\[=0.49+0.4\]\[=0.89\,Newton\] Problem 173. A body of mass \[2kg\] is moving in a vertical circle of radius \[2m\]. The work done when it moves from the lowest point to the highest point is (a) \[80\ J\] (b) \[40\ J\] (c) \[20\ J\] (d) 0 Solution: (a) work done = change in potential energy \[=2\,mgr\]\[=2\times 2\times 10\times 2\]\[=80\,J\] Problem 174. A body of mass \[m\] is tied to one end of a string of length \[l\] and revolves vertically in a circular path. At the lowest point of circle, what must be the K.E. of the body so as to complete the circle [RPMT 1996] (a) \[5\ mgl\] (b) \[4\ mgl\] (c) \[2.5\ mgl\] (d) \[2\ mgl\] Solution: (c) Minimum velocity at lowest point to complete vertical loop \[=\sqrt{5\,gl}\] So minimum kinetic energy \[=\frac{1}{2}m\,({{v}^{2}})\] \[=\frac{1}{2}m\,{{(\sqrt{5gl})}^{2}}\]\[=\frac{5}{2}mgl\]\[=2.5\,mgl\]
You need to login to perform this action.
You will be redirected in
3 sec
