Conical Pendulum
Category : NEET
Conical Pendulum This is the example of uniform circular motion in horizontal plane. A bob of mass m attached to a light and in-extensible string rotates in a horizontal circle of radius r with constant angular speed w about the vertical. The string makes angle \[\theta \] with vertical and appears tracing the surface of a cone. So this arrangement is called conical pendulum. The force acting on the bob are tension and weight of the bob. 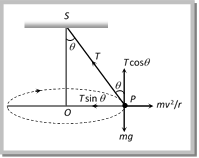 From the figure \[T\sin \theta =\frac{m{{v}^{2}}}{r}\] ?. (i) and \[T\cos \theta =mg\] ?. (ii) Tension in the string: \[T=mg\sqrt{1+{{\left( \frac{{{v}^{2}}}{rg} \right)}^{2}}}\]
From the figure \[T\sin \theta =\frac{m{{v}^{2}}}{r}\] ?. (i) and \[T\cos \theta =mg\] ?. (ii) Tension in the string: \[T=mg\sqrt{1+{{\left( \frac{{{v}^{2}}}{rg} \right)}^{2}}}\] 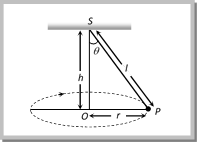 \[T=\frac{mg}{\cos \theta }=\frac{mgl}{\sqrt{{{l}^{2}}-{{r}^{2}}}}\] [As \[\cos \theta =\frac{h}{l}=\frac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}\]] (2) Angle of string from the vertical: \[\tan \theta =\frac{{{v}^{2}}}{rg}\] (3) Linear velocity of the bob: \[v=\sqrt{gr\tan \theta }\] (4) Angular velocity of the bob: \[\omega =\sqrt{\frac{g}{r}\tan \theta }=\sqrt{\frac{g}{h}}=\sqrt{\frac{g}{l\cos \theta }}\] (5) Time period of revolution: \[{{T}_{P}}=2\pi \sqrt{\frac{l\cos \theta }{g}}=2\pi \sqrt{\frac{h}{g}}=2\pi \sqrt{\frac{{{l}^{2}}-{{r}^{2}}}{g}}=2\pi \sqrt{\frac{r}{g\tan \theta }}\] Sample problems based on conical pendulum Problem 175. A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are [AMU (Med.) 2001]
\[T=\frac{mg}{\cos \theta }=\frac{mgl}{\sqrt{{{l}^{2}}-{{r}^{2}}}}\] [As \[\cos \theta =\frac{h}{l}=\frac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}\]] (2) Angle of string from the vertical: \[\tan \theta =\frac{{{v}^{2}}}{rg}\] (3) Linear velocity of the bob: \[v=\sqrt{gr\tan \theta }\] (4) Angular velocity of the bob: \[\omega =\sqrt{\frac{g}{r}\tan \theta }=\sqrt{\frac{g}{h}}=\sqrt{\frac{g}{l\cos \theta }}\] (5) Time period of revolution: \[{{T}_{P}}=2\pi \sqrt{\frac{l\cos \theta }{g}}=2\pi \sqrt{\frac{h}{g}}=2\pi \sqrt{\frac{{{l}^{2}}-{{r}^{2}}}{g}}=2\pi \sqrt{\frac{r}{g\tan \theta }}\] Sample problems based on conical pendulum Problem 175. A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are [AMU (Med.) 2001] 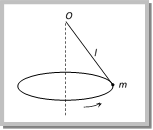 (a)
(a) 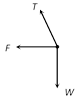 (b)
(b) ![]() (c)
(c) 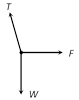 (d)
(d) 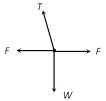 Solution: (c) Centrifugal force (F) works radially outward, Weight (w) works downward Tension (T) work along the string and towards the point of suspension Problem 176. A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/p revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is [BHU 2002]
Solution: (c) Centrifugal force (F) works radially outward, Weight (w) works downward Tension (T) work along the string and towards the point of suspension Problem 176. A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/p revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is [BHU 2002] 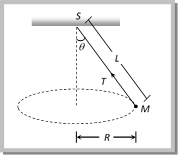 (a) ML (b) 2 ML (c) 4 ML (d) 16 ML Solution: (d) \[T\sin \theta =M{{\omega }^{2}}R\] ..... (i) \[T\,\sin \,\theta \,=\,M{{\omega }^{2}}L\sin \theta \] ..... (ii)
(a) ML (b) 2 ML (c) 4 ML (d) 16 ML Solution: (d) \[T\sin \theta =M{{\omega }^{2}}R\] ..... (i) \[T\,\sin \,\theta \,=\,M{{\omega }^{2}}L\sin \theta \] ..... (ii) 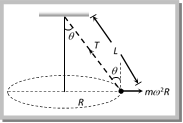 From (i) and (ii) \[T=M{{\omega }^{2}}L\]\[=M4{{\pi }^{2}}{{n}^{2}}L\] \[=M4{{\pi }^{2}}{{\left( \frac{2}{\pi } \right)}^{2}}L\]\[=16ML\] Problem 177. A string of length \[1m\] is fixed at one end and a mass of \[100gm\] is attached at the other end. The string makes \[2/\pi \] rev/sec around a vertical axis through the fixed point. The angle of inclination of the string with the vertical is (\[g=10\ m/{{\sec }^{2}}\]) (a) \[{{\tan }^{-1}}\frac{5}{8}\] (b) \[{{\tan }^{-1}}\frac{8}{5}\] (c) \[{{\cos }^{-1}}\frac{8}{5}\] (d) \[{{\cos }^{-1}}\frac{5}{8}\]
From (i) and (ii) \[T=M{{\omega }^{2}}L\]\[=M4{{\pi }^{2}}{{n}^{2}}L\] \[=M4{{\pi }^{2}}{{\left( \frac{2}{\pi } \right)}^{2}}L\]\[=16ML\] Problem 177. A string of length \[1m\] is fixed at one end and a mass of \[100gm\] is attached at the other end. The string makes \[2/\pi \] rev/sec around a vertical axis through the fixed point. The angle of inclination of the string with the vertical is (\[g=10\ m/{{\sec }^{2}}\]) (a) \[{{\tan }^{-1}}\frac{5}{8}\] (b) \[{{\tan }^{-1}}\frac{8}{5}\] (c) \[{{\cos }^{-1}}\frac{8}{5}\] (d) \[{{\cos }^{-1}}\frac{5}{8}\] 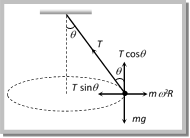 Solution: (d) For the critical condition, in equilibrium \[T\sin \theta =m\,{{\omega }^{2}}r\] and \[T\cos \theta =mg\] \[\therefore \,\,\tan \theta =\frac{{{\omega }^{2}}r}{g}\] \[\Rightarrow \,\,\frac{4{{\pi }^{2}}{{n}^{2}}r}{g}=\frac{4{{\pi }^{2}}{{(2/\pi )}^{2}}\,.\,1}{10}=\frac{8}{5}\] Sample problems (Miscellaneous) Problem 178. If the frequency of the rotating platform is f and the distance of a boy from the centre is r, which is the area swept out per second by line connecting the boy to the centre (a) \[\pi rf\] (b) \[2\pi rf\] (c) \[\pi {{r}^{2}}f\] (d) \[2\pi {{r}^{2}}f\] Solution: (c) Area swept by line in complete revolution \[=\pi {{r}^{2}}\] If frequency of rotating platform is f per second, then Area swept will be \[\pi \,{{r}^{2}}f\] per second. Problem 179. Figure below shows a body of mass M moving with uniform speed v along a circle of radius R. What is the change in speed in going from \[{{\operatorname{P}}_{1}}\,\,to\, {{P}_{2}}\].
Solution: (d) For the critical condition, in equilibrium \[T\sin \theta =m\,{{\omega }^{2}}r\] and \[T\cos \theta =mg\] \[\therefore \,\,\tan \theta =\frac{{{\omega }^{2}}r}{g}\] \[\Rightarrow \,\,\frac{4{{\pi }^{2}}{{n}^{2}}r}{g}=\frac{4{{\pi }^{2}}{{(2/\pi )}^{2}}\,.\,1}{10}=\frac{8}{5}\] Sample problems (Miscellaneous) Problem 178. If the frequency of the rotating platform is f and the distance of a boy from the centre is r, which is the area swept out per second by line connecting the boy to the centre (a) \[\pi rf\] (b) \[2\pi rf\] (c) \[\pi {{r}^{2}}f\] (d) \[2\pi {{r}^{2}}f\] Solution: (c) Area swept by line in complete revolution \[=\pi {{r}^{2}}\] If frequency of rotating platform is f per second, then Area swept will be \[\pi \,{{r}^{2}}f\] per second. Problem 179. Figure below shows a body of mass M moving with uniform speed v along a circle of radius R. What is the change in speed in going from \[{{\operatorname{P}}_{1}}\,\,to\, {{P}_{2}}\]. 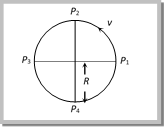 (a) Zero (b) \[\sqrt{2v}\] (c) \[v/\sqrt{2}\] (d) \[2\,v\] Solution: (a) In uniform circular motion speed remain constant. \[\therefore \] change in speed is zero. Problem 180. In the above problem, what is change in velocity in going from \[{{\operatorname{P}}_{1\,\,}}to {{P}_{2}}\] (a) Zero (b) \[\sqrt{2v}\] (c) \[v/\sqrt{2}\] (d) 2 v Solution: (b) Change in velocity \[=2v\sin (\theta /2)\]\[=2v\sin \left( \frac{90}{2} \right)\]\[=2v\sin 45\]\[=\frac{2v}{\sqrt{2}}\]\[=\sqrt{2}\,v\] Problem 181. In the above problem, what is the change in angular velocity in going from P1 to P2 (a) Zero (b) \[\sqrt{2}\,v/R\] (c) \[v/\sqrt{2}\,R\] (d) \[2\,v/R\] Solution: (a) Angular velocity remains constant, so change in angular velocity = Zero. Problem 182. A particle of mass \[m\] is fixed to one end of a light spring of force constant \[k\] and unstretched length \[l\]. The system is rotated about the other end of the spring with an angular velocity \[\omega \], in gravity free space. The increase in length of the spring will be (a) \[\frac{m{{\omega }^{2}}l}{k}\] (b) \[\frac{m{{\omega }^{2}}l}{k-m{{\omega }^{2}}}\] (c) \[\frac{m{{\omega }^{2}}l}{k+m{{\omega }^{2}}}\] (d) None of these
(a) Zero (b) \[\sqrt{2v}\] (c) \[v/\sqrt{2}\] (d) \[2\,v\] Solution: (a) In uniform circular motion speed remain constant. \[\therefore \] change in speed is zero. Problem 180. In the above problem, what is change in velocity in going from \[{{\operatorname{P}}_{1\,\,}}to {{P}_{2}}\] (a) Zero (b) \[\sqrt{2v}\] (c) \[v/\sqrt{2}\] (d) 2 v Solution: (b) Change in velocity \[=2v\sin (\theta /2)\]\[=2v\sin \left( \frac{90}{2} \right)\]\[=2v\sin 45\]\[=\frac{2v}{\sqrt{2}}\]\[=\sqrt{2}\,v\] Problem 181. In the above problem, what is the change in angular velocity in going from P1 to P2 (a) Zero (b) \[\sqrt{2}\,v/R\] (c) \[v/\sqrt{2}\,R\] (d) \[2\,v/R\] Solution: (a) Angular velocity remains constant, so change in angular velocity = Zero. Problem 182. A particle of mass \[m\] is fixed to one end of a light spring of force constant \[k\] and unstretched length \[l\]. The system is rotated about the other end of the spring with an angular velocity \[\omega \], in gravity free space. The increase in length of the spring will be (a) \[\frac{m{{\omega }^{2}}l}{k}\] (b) \[\frac{m{{\omega }^{2}}l}{k-m{{\omega }^{2}}}\] (c) \[\frac{m{{\omega }^{2}}l}{k+m{{\omega }^{2}}}\] (d) None of these 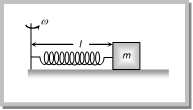 Solution: (b) In the given condition elastic force will provides the required centripetal force
Solution: (b) In the given condition elastic force will provides the required centripetal force 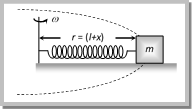 \[k\,x=m\,{{\omega }^{2}}r\] \[k\,x=m\,{{\omega }^{2}}(l+x)\Rightarrow k\,x=m{{\omega }^{2}}l+m\,{{\omega }^{2}}x\] \[\Rightarrow \] \[x(k-m\,{{\omega }^{2}})=m\,{{\omega }^{2}}l\] \[\therefore \,\,x=\frac{m\,{{\omega }^{2}}l}{k-m\,{{\omega }^{2}}}\] Problem 183. A uniform rod of mass \[m\] and length \[l\] rotates in a horizontal plane with an angular velocity \[\omega \] about a vertical axis passing through one end. The tension in the rod at a distance \[x\] from the axis is (a) \[\frac{1}{2}\ m{{\omega }^{2}}x\] (b) \[\frac{1}{2}\ m{{\omega }^{2}}\frac{{{x}^{2}}}{l}\] (c) \[\frac{1}{2}m{{\omega }^{2}}l\left( 1-\frac{x}{l} \right)\] (d) \[\frac{1}{2}\frac{m{{\omega }^{2}}}{l}[{{l}^{2}}-{{x}^{2}}]\] Solution: (d) Let rod AB performs uniform circular motion about point A. We have to calculate the tension in the rod at a distance x from the axis of rotation. Let mass of the small segment at a distance x is dm
\[k\,x=m\,{{\omega }^{2}}r\] \[k\,x=m\,{{\omega }^{2}}(l+x)\Rightarrow k\,x=m{{\omega }^{2}}l+m\,{{\omega }^{2}}x\] \[\Rightarrow \] \[x(k-m\,{{\omega }^{2}})=m\,{{\omega }^{2}}l\] \[\therefore \,\,x=\frac{m\,{{\omega }^{2}}l}{k-m\,{{\omega }^{2}}}\] Problem 183. A uniform rod of mass \[m\] and length \[l\] rotates in a horizontal plane with an angular velocity \[\omega \] about a vertical axis passing through one end. The tension in the rod at a distance \[x\] from the axis is (a) \[\frac{1}{2}\ m{{\omega }^{2}}x\] (b) \[\frac{1}{2}\ m{{\omega }^{2}}\frac{{{x}^{2}}}{l}\] (c) \[\frac{1}{2}m{{\omega }^{2}}l\left( 1-\frac{x}{l} \right)\] (d) \[\frac{1}{2}\frac{m{{\omega }^{2}}}{l}[{{l}^{2}}-{{x}^{2}}]\] Solution: (d) Let rod AB performs uniform circular motion about point A. We have to calculate the tension in the rod at a distance x from the axis of rotation. Let mass of the small segment at a distance x is dm 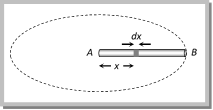 So \[dT=dm\,{{\omega }^{2}}x\]\[=\left( \frac{m}{l} \right)\,dx\,.\,{{\omega }^{2}}x\]\[=\frac{m\,{{\omega }^{2}}}{l}\] [x d x] Integrating both sides \[\int\limits_{x}^{l}{dT}=\frac{m\,{{\omega }^{2}}}{l}\int\limits_{x}^{l}{x\,dx}\]\[\Rightarrow \]\[T=\frac{m{{\omega }^{2}}}{l}\left[ \frac{{{x}^{2}}}{2} \right]_{x}^{l}\] \[\therefore \,\,\,T=\frac{m\,{{\omega }^{2}}}{2l}\left[ \,{{l}^{2}}-{{x}^{2}} \right]\] Problem 184. A long horizontal rod has a bead which can slide along its length, and initially placed at a distance \[L\] from one end \[A\] of the rod. The rod is set in angular motion about A with constant angular acceleration \[\alpha \]. If the coefficient of friction between the rod and the bead is \[\mu \], and gravity is neglected, then the time after which the bead starts slipping is [IIT-JEE (Screening) 2000] (a) \[\sqrt{\frac{\mu }{\alpha }}\] (b) \[\frac{\mu }{\sqrt{\alpha }}\] (c) \[\frac{1}{\sqrt{\mu \alpha }}\] (d) Infinitesimal Solution: (a) Let the bead starts slipping after time t
So \[dT=dm\,{{\omega }^{2}}x\]\[=\left( \frac{m}{l} \right)\,dx\,.\,{{\omega }^{2}}x\]\[=\frac{m\,{{\omega }^{2}}}{l}\] [x d x] Integrating both sides \[\int\limits_{x}^{l}{dT}=\frac{m\,{{\omega }^{2}}}{l}\int\limits_{x}^{l}{x\,dx}\]\[\Rightarrow \]\[T=\frac{m{{\omega }^{2}}}{l}\left[ \frac{{{x}^{2}}}{2} \right]_{x}^{l}\] \[\therefore \,\,\,T=\frac{m\,{{\omega }^{2}}}{2l}\left[ \,{{l}^{2}}-{{x}^{2}} \right]\] Problem 184. A long horizontal rod has a bead which can slide along its length, and initially placed at a distance \[L\] from one end \[A\] of the rod. The rod is set in angular motion about A with constant angular acceleration \[\alpha \]. If the coefficient of friction between the rod and the bead is \[\mu \], and gravity is neglected, then the time after which the bead starts slipping is [IIT-JEE (Screening) 2000] (a) \[\sqrt{\frac{\mu }{\alpha }}\] (b) \[\frac{\mu }{\sqrt{\alpha }}\] (c) \[\frac{1}{\sqrt{\mu \alpha }}\] (d) Infinitesimal Solution: (a) Let the bead starts slipping after time t 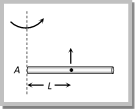 For critical condition Frictional force provides the centripetal force \[m{{\omega }^{2}}L=\mu \,R\]\[=\mu \,m\times {{a}_{t}}=\mu mL\alpha \] m (at)2L = mmLa Þ \[t=\sqrt{\frac{\mu }{\alpha }}\] (As w = at) Problem 185. A smooth table is placed horizontally and an ideal spring of spring constant \[k=1000\ N/m\] and unextended length of \[0.5m\] has one end fixed to its centre. The other end is attached to a mass of \[5kg\] which is moving in a circle with constant speed \[20m/s\]. Then the tension in the spring and the extension of this spring beyond its normal length are (a) \[500\ N,\ 0.5\ m\] (b) \[600\ N,\ 0.6\ m\] (c) \[700\ N,\ 0.7\ m\] (d) \[800\ N,\ 0.8\ m\] Solution: (a) \[k=1000,\] \[m=5\,kg,\] \[l=0.5\,m,\] \[v=20\,m/s\] (given) Restoring force \[= kx=\frac{m\,{{v}^{2}}}{r}=\frac{m\,{{v}^{2}}}{l+x}\Rightarrow 1000\,x=\frac{5\,{{(20)}^{2}}}{0.5+x}\Rightarrow x=0.5\,\,m\] and Tension in the spring \[=kx=1000\times \frac{1}{2}=500\,N\] Problem 186. A particle describes a horizontal circle at the mouth of a funnel type vessel as shown in figure. The surface of the funnel is frictionless. The velocity \[v\] of the particle in terms of \[r\] and \[\theta \] will be
For critical condition Frictional force provides the centripetal force \[m{{\omega }^{2}}L=\mu \,R\]\[=\mu \,m\times {{a}_{t}}=\mu mL\alpha \] m (at)2L = mmLa Þ \[t=\sqrt{\frac{\mu }{\alpha }}\] (As w = at) Problem 185. A smooth table is placed horizontally and an ideal spring of spring constant \[k=1000\ N/m\] and unextended length of \[0.5m\] has one end fixed to its centre. The other end is attached to a mass of \[5kg\] which is moving in a circle with constant speed \[20m/s\]. Then the tension in the spring and the extension of this spring beyond its normal length are (a) \[500\ N,\ 0.5\ m\] (b) \[600\ N,\ 0.6\ m\] (c) \[700\ N,\ 0.7\ m\] (d) \[800\ N,\ 0.8\ m\] Solution: (a) \[k=1000,\] \[m=5\,kg,\] \[l=0.5\,m,\] \[v=20\,m/s\] (given) Restoring force \[= kx=\frac{m\,{{v}^{2}}}{r}=\frac{m\,{{v}^{2}}}{l+x}\Rightarrow 1000\,x=\frac{5\,{{(20)}^{2}}}{0.5+x}\Rightarrow x=0.5\,\,m\] and Tension in the spring \[=kx=1000\times \frac{1}{2}=500\,N\] Problem 186. A particle describes a horizontal circle at the mouth of a funnel type vessel as shown in figure. The surface of the funnel is frictionless. The velocity \[v\] of the particle in terms of \[r\] and \[\theta \] will be 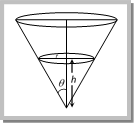 (a) \[v=\sqrt{rg/\tan \ \theta }\] (b) \[v=\sqrt{rg\ \tan \theta }\] (c) \[v=\sqrt{rg\ \cot \theta }\] (d) \[v=\sqrt{rg}/\cot \theta \] Solution: (c) For uniform circular motion of a particle \[\frac{m\,{{v}^{2}}}{r}=R\cos \theta \] ?. (i)
(a) \[v=\sqrt{rg/\tan \ \theta }\] (b) \[v=\sqrt{rg\ \tan \theta }\] (c) \[v=\sqrt{rg\ \cot \theta }\] (d) \[v=\sqrt{rg}/\cot \theta \] Solution: (c) For uniform circular motion of a particle \[\frac{m\,{{v}^{2}}}{r}=R\cos \theta \] ?. (i) 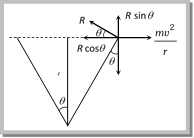 and \[mg=R\sin \theta \] ?. (ii) Dividing (i) by (ii) \[\frac{{{v}^{2}}}{rg}=\cot \theta \]\[\Rightarrow \,\,v=\sqrt{rg\cot \theta }\] Problem 187. Figure shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring constant \[k\] fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P [see. Fig], where the radius of the track is horizontal
and \[mg=R\sin \theta \] ?. (ii) Dividing (i) by (ii) \[\frac{{{v}^{2}}}{rg}=\cot \theta \]\[\Rightarrow \,\,v=\sqrt{rg\cot \theta }\] Problem 187. Figure shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring constant \[k\] fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P [see. Fig], where the radius of the track is horizontal 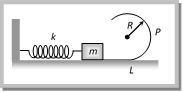 (a) \[\sqrt{\frac{mgR}{3k}}\] (b) \[\sqrt{\frac{3gR}{mk}}\] (c) \[\sqrt{\frac{3mgR}{k}}\] (d) \[\sqrt{\frac{3mg}{kR}}\] Solution: (c) For the given condition, centrifugal force at P should be equal to mg i.e. \[\frac{mv_{P}^{2}}{R}=mg\]\[\therefore \,\,{{v}_{P}}=\sqrt{Rg}\] From this we can easily calculate the required velocity at the lowest point of circular track. \[v_{p}^{2}=v_{L}^{2}-2gR\] (by using formula : \[{{v}^{2}}={{u}^{2}}-2gh\]) \[{{v}_{L}}=\sqrt{v_{P}^{2}+2gR}=\sqrt{Rg+2gR}=\sqrt{3gR}\] It means the block should possess kinetic energy \[=\frac{1}{2}\,mv_{L}^{2}\]\[=\frac{1}{2}\,m\,\times 3gR\] And by the law of conservation of energy \[\frac{1}{2}k{{x}^{2}}=\frac{1}{2}\,3m\times \,g\,R\Rightarrow \,x=\sqrt{\frac{3m\,g\,R}{k}}\].
(a) \[\sqrt{\frac{mgR}{3k}}\] (b) \[\sqrt{\frac{3gR}{mk}}\] (c) \[\sqrt{\frac{3mgR}{k}}\] (d) \[\sqrt{\frac{3mg}{kR}}\] Solution: (c) For the given condition, centrifugal force at P should be equal to mg i.e. \[\frac{mv_{P}^{2}}{R}=mg\]\[\therefore \,\,{{v}_{P}}=\sqrt{Rg}\] From this we can easily calculate the required velocity at the lowest point of circular track. \[v_{p}^{2}=v_{L}^{2}-2gR\] (by using formula : \[{{v}^{2}}={{u}^{2}}-2gh\]) \[{{v}_{L}}=\sqrt{v_{P}^{2}+2gR}=\sqrt{Rg+2gR}=\sqrt{3gR}\] It means the block should possess kinetic energy \[=\frac{1}{2}\,mv_{L}^{2}\]\[=\frac{1}{2}\,m\,\times 3gR\] And by the law of conservation of energy \[\frac{1}{2}k{{x}^{2}}=\frac{1}{2}\,3m\times \,g\,R\Rightarrow \,x=\sqrt{\frac{3m\,g\,R}{k}}\].
You need to login to perform this action.
You will be redirected in
3 sec
