Centripetal Acceleration and Force
Category : NEET
Centripetal Acceleration and Force (1) Acceleration acting on the object undergoing uniform circular motion is called centripetal acceleration. (2) It always acts on the object along the radius towards the centre of the circular path. (3) Magnitude of centripetal acceleration \[a\,=\frac{{{v}^{2}}}{r}={{\omega }^{2}}r=4\pi {{n}^{2}}r=\frac{4{{\pi }^{2}}}{{{T}^{2}}}r\] 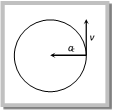 (4) Direction of centripetal acceleration: It is always the same as that of \[\Delta \overrightarrow{\upsilon }\]. When Dt decreases, Dq also decreases. Due to which \[\Delta \vec{\upsilon }\] becomes more and more perpendicular to \[\overrightarrow{\upsilon }\]. When \[\Delta t\to 0\], \[\Delta \overrightarrow{\upsilon }\] becomes perpendicular to the velocity vector. As the velocity vector of the particle at an instant acts along the tangent to the circular path, therefore \[\Delta \overrightarrow{\upsilon }\] and hence the centripetal acceleration vector acts along the radius of the circular path at that point and is directed towards the centre of the circular path. Sample problems based on centripetal acceleration Problem 100. If a cycle wheel of radius 4 m completes one revolution in two seconds. Then acceleration of the cycle will be [Pb. PMT 2001] (a) \[{{\pi }^{2}}m/{{s}^{2}}\] (b) \[2{{\pi }^{2}}m/{{s}^{2}}\] (c) \[4{{\pi }^{2}}m/{{s}^{2}}\] (d) \[8\pi \,m/{{s}^{2}}\] Solution: (c) Given \[r=4\,m\] and \[T=2\,\,\sec onds.\] \[\therefore \,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}4=4{{\pi }^{2}}\,m/{{s}^{2}}\] Problem 101. A stone is tied to one end of a spring 50 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 10 revolutions in 20 s, what is the magnitude of acceleration of the stone [Pb. PMT 2000] (a) \[493 cm/se{{c}^{2}}\] (b) \[720\text{ }cm/se{{c}^{2}}\] (c) \[860 cm/se{{c}^{2}}\] (d) \[990 cm/se{{c}^{2}}\] Solution: (a) \[=\frac{\text{Total time}}{\text{No}\text{. of revolution}}=\frac{20}{10}=2\,sec\] \[\therefore \,\,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}.r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}\times (1/2)\,m/{{s}^{2}}=4.93\,m/{{s}^{2}}=493\,cm/{{s}^{2}}\] Problem 102. A particle moves with a constant speed v along a circular path of radius r and completes the circle in time T. What is the acceleration of the particle [Orissa JEE 2002] (a) \[mg\] (b) \[\frac{2\pi v}{T}\] (c) \[\frac{\pi {{r}^{2}}}{T}\] (d) \[\frac{\pi {{v}^{2}}}{T}\] Solution: (b) \[{{a}_{c}}=\frac{{{v}^{2}}}{r}={{\omega }^{2}}r=v\omega =v\,\left( \frac{2\pi }{T} \right)=\frac{2\pi \,v}{T}\] Problem 103. If the speed of revolution of a particle on the circumference of a circle and the speed gained in falling through a distance equal to half the radius are equal, then the centripetal acceleration will be (a) \[\frac{g}{2}\] (b) \[\frac{g}{4}\] (c) \[\frac{g}{3}\] (d) g Solution: (d) Speed gain by body falling through a distance h is equal to \[v=\sqrt{2gh}=\sqrt{2g\frac{r}{2}}\] [As \[h=\frac{r}{2}\] given] \[\Rightarrow v=\sqrt{gr}\Rightarrow \,\,\frac{{{v}^{2}}}{r}=g\] Problem 104. Two cars going round curve with speeds one at 90 km/h and other at 15 km/h. Each car experiences same acceleration. The radii of curves are in the ratio of [EAMCET (Med.) 1998] (a) 4 : 1 (b) 2 : 1 (c) 16 : 1 (d) 36 : 1 Solution: (d) Centripetal acceleration \[=\frac{v_{1}^{2}}{{{r}_{1}}}=\frac{v_{2}^{2}}{{{r}_{2}}}\] (given) \[\therefore \,\,\,\,\frac{{{r}_{1}}}{{{r}_{2}}}={{\left( \frac{{{v}_{1}}}{{{v}_{2}}} \right)}^{2}}={{\left( \frac{90}{15} \right)}^{2}}=\frac{36}{1}\] Problem 105. A wheel of radius \[0.20\,\,m\] is accelerated from rest with an angular acceleration of \[1\ rad/{{s}^{2}}\]. After a rotation of \[{{90}^{o}}\] the radial acceleration of a particle on its rim will be (a) \[\pi \ m/{{s}^{2}}\] (b) \[0.5\ \pi \ m/{{s}^{2}}\] (c) \[2.0\,\,\pi \ m/{{s}^{2}}\] (d) \[0.2\ \pi \ m/{{s}^{2}}\] Solution: (d) From the equation of motion Angular speed acquired by the wheel, \[\omega _{2}^{2}=\omega _{1}^{2}+2\alpha \theta =0+2\times 1\times \frac{\pi }{2}\Rightarrow \omega _{2}^{2}=\pi \] Now radial acceleration \[{{\omega }^{2}}r=\pi \times 0.2=0.2\pi \,m/{{s}^{2}}\] Centripetal Force. According to Newton?s first law of motion, whenever a body moves in a straight line with uniform velocity, no force is required to maintain this velocity. But when a body moves along a circular path with uniform speed, its direction changes continuously i.e. velocity keeps on changing on account of a change in direction. According to Newton?s second law of motion, a change in the direction of motion of the body can take place only if some external force acts on the body. Due to inertia, at every point of the circular path; the body tends to move along the tangent to the circular path at that point (in figure). Since everybody has directional inertia, a velocity cannot change by itself and as such we have to apply a force. But this force should be such that it changes the direction of velocity and not its magnitude. This is possible only if the force acts perpendicular to the direction of velocity. Because the velocity is along the tangent, this force must be along the radius (because the radius of a circle at any point is perpendicular to the tangent at that point). Further, as this force is to move the body in a circular path, it must acts towards the centre. This centre-seeking force is called the centripetal force.
(4) Direction of centripetal acceleration: It is always the same as that of \[\Delta \overrightarrow{\upsilon }\]. When Dt decreases, Dq also decreases. Due to which \[\Delta \vec{\upsilon }\] becomes more and more perpendicular to \[\overrightarrow{\upsilon }\]. When \[\Delta t\to 0\], \[\Delta \overrightarrow{\upsilon }\] becomes perpendicular to the velocity vector. As the velocity vector of the particle at an instant acts along the tangent to the circular path, therefore \[\Delta \overrightarrow{\upsilon }\] and hence the centripetal acceleration vector acts along the radius of the circular path at that point and is directed towards the centre of the circular path. Sample problems based on centripetal acceleration Problem 100. If a cycle wheel of radius 4 m completes one revolution in two seconds. Then acceleration of the cycle will be [Pb. PMT 2001] (a) \[{{\pi }^{2}}m/{{s}^{2}}\] (b) \[2{{\pi }^{2}}m/{{s}^{2}}\] (c) \[4{{\pi }^{2}}m/{{s}^{2}}\] (d) \[8\pi \,m/{{s}^{2}}\] Solution: (c) Given \[r=4\,m\] and \[T=2\,\,\sec onds.\] \[\therefore \,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}4=4{{\pi }^{2}}\,m/{{s}^{2}}\] Problem 101. A stone is tied to one end of a spring 50 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 10 revolutions in 20 s, what is the magnitude of acceleration of the stone [Pb. PMT 2000] (a) \[493 cm/se{{c}^{2}}\] (b) \[720\text{ }cm/se{{c}^{2}}\] (c) \[860 cm/se{{c}^{2}}\] (d) \[990 cm/se{{c}^{2}}\] Solution: (a) \[=\frac{\text{Total time}}{\text{No}\text{. of revolution}}=\frac{20}{10}=2\,sec\] \[\therefore \,\,\,\,\,{{a}_{c}}=\frac{4{{\pi }^{2}}}{{{T}^{2}}}.r=\frac{4{{\pi }^{2}}}{{{(2)}^{2}}}\times (1/2)\,m/{{s}^{2}}=4.93\,m/{{s}^{2}}=493\,cm/{{s}^{2}}\] Problem 102. A particle moves with a constant speed v along a circular path of radius r and completes the circle in time T. What is the acceleration of the particle [Orissa JEE 2002] (a) \[mg\] (b) \[\frac{2\pi v}{T}\] (c) \[\frac{\pi {{r}^{2}}}{T}\] (d) \[\frac{\pi {{v}^{2}}}{T}\] Solution: (b) \[{{a}_{c}}=\frac{{{v}^{2}}}{r}={{\omega }^{2}}r=v\omega =v\,\left( \frac{2\pi }{T} \right)=\frac{2\pi \,v}{T}\] Problem 103. If the speed of revolution of a particle on the circumference of a circle and the speed gained in falling through a distance equal to half the radius are equal, then the centripetal acceleration will be (a) \[\frac{g}{2}\] (b) \[\frac{g}{4}\] (c) \[\frac{g}{3}\] (d) g Solution: (d) Speed gain by body falling through a distance h is equal to \[v=\sqrt{2gh}=\sqrt{2g\frac{r}{2}}\] [As \[h=\frac{r}{2}\] given] \[\Rightarrow v=\sqrt{gr}\Rightarrow \,\,\frac{{{v}^{2}}}{r}=g\] Problem 104. Two cars going round curve with speeds one at 90 km/h and other at 15 km/h. Each car experiences same acceleration. The radii of curves are in the ratio of [EAMCET (Med.) 1998] (a) 4 : 1 (b) 2 : 1 (c) 16 : 1 (d) 36 : 1 Solution: (d) Centripetal acceleration \[=\frac{v_{1}^{2}}{{{r}_{1}}}=\frac{v_{2}^{2}}{{{r}_{2}}}\] (given) \[\therefore \,\,\,\,\frac{{{r}_{1}}}{{{r}_{2}}}={{\left( \frac{{{v}_{1}}}{{{v}_{2}}} \right)}^{2}}={{\left( \frac{90}{15} \right)}^{2}}=\frac{36}{1}\] Problem 105. A wheel of radius \[0.20\,\,m\] is accelerated from rest with an angular acceleration of \[1\ rad/{{s}^{2}}\]. After a rotation of \[{{90}^{o}}\] the radial acceleration of a particle on its rim will be (a) \[\pi \ m/{{s}^{2}}\] (b) \[0.5\ \pi \ m/{{s}^{2}}\] (c) \[2.0\,\,\pi \ m/{{s}^{2}}\] (d) \[0.2\ \pi \ m/{{s}^{2}}\] Solution: (d) From the equation of motion Angular speed acquired by the wheel, \[\omega _{2}^{2}=\omega _{1}^{2}+2\alpha \theta =0+2\times 1\times \frac{\pi }{2}\Rightarrow \omega _{2}^{2}=\pi \] Now radial acceleration \[{{\omega }^{2}}r=\pi \times 0.2=0.2\pi \,m/{{s}^{2}}\] Centripetal Force. According to Newton?s first law of motion, whenever a body moves in a straight line with uniform velocity, no force is required to maintain this velocity. But when a body moves along a circular path with uniform speed, its direction changes continuously i.e. velocity keeps on changing on account of a change in direction. According to Newton?s second law of motion, a change in the direction of motion of the body can take place only if some external force acts on the body. Due to inertia, at every point of the circular path; the body tends to move along the tangent to the circular path at that point (in figure). Since everybody has directional inertia, a velocity cannot change by itself and as such we have to apply a force. But this force should be such that it changes the direction of velocity and not its magnitude. This is possible only if the force acts perpendicular to the direction of velocity. Because the velocity is along the tangent, this force must be along the radius (because the radius of a circle at any point is perpendicular to the tangent at that point). Further, as this force is to move the body in a circular path, it must acts towards the centre. This centre-seeking force is called the centripetal force. 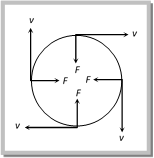 Hence, centripetal force is that force which is required to move a body in a circular path with uniform speed. The force acts on the body along the radius and towards centre. (1) Formulae for centripetal force: \[F=\frac{m{{v}^{2}}}{r}=m{{\omega }^{2}}r=m\,4{{\pi }^{2}}{{n}^{2}}r=\frac{m4{{\pi }^{2}}r}{{{T}^{2}}}\] (2) Centripetal force in different situation
Hence, centripetal force is that force which is required to move a body in a circular path with uniform speed. The force acts on the body along the radius and towards centre. (1) Formulae for centripetal force: \[F=\frac{m{{v}^{2}}}{r}=m{{\omega }^{2}}r=m\,4{{\pi }^{2}}{{n}^{2}}r=\frac{m4{{\pi }^{2}}r}{{{T}^{2}}}\] (2) Centripetal force in different situation
| Situation | Centripetal Force |
| A particle tied to a string and whirled in a horizontal circle | Tension in the string |
| Vehicle taking a turn on a level road | Frictional force exerted by the road on the tyres |
| A vehicle on a speed breaker | Weight of the body or a component of weight |
| Revolution of earth around the sun | Gravitational force exerted by the sun |
| Electron revolving around the nucleus in an atom | Coulomb attraction exerted by the protons in the nucleus |
| A charged particle describing a circular path in a magnetic field | Magnetic force exerted by the agent that sets up the magnetic field |
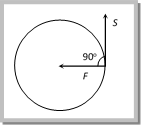 Also \[W=\overrightarrow{F}\,.\,\overrightarrow{S}=\text{ }F\,.\,S\,cos\,\theta \] \[=\,\, F\,.\,S cos{{90}^{o}}=\text{ }0\] Example: (i) When an electron revolve around the nucleus in hydrogen atom in a particular orbit, it neither absorb nor emit any energy means its energy remains constant. (ii) When a satellite established once in a orbit around the earth and it starts revolving with particular speed, then no fuel is required for its circular motion. Sample problem based on work done Problem 121. A particle does uniform circular motion in a horizontal plane. The radius of the circle is 20 cm. The centripetal force acting on the particle is 10 N. It?s kinetic energy is (a) 0.1 Joule (b) 0.2 Joule (c) 2.0 Joule (d) 1.0 Joule Solution: (d) \[\frac{m\,{{v}^{2}}}{r}=10\,N\] (given) \[\Rightarrow m\,{{v}^{2}}=10\times r=10\times 0.2=2\] Kinetic energy \[\frac{1}{2}m\,{{v}^{2}}=\frac{1}{2}(2)=1\,Joule.\] Problem 122. A body of mass 100 g is rotating in a circular path of radius r with constant velocity. The work done in one complete revolution is [AFMC 1998] (a) 100r Joule (b) (r/100) Joule (c) (100/r) Joule (d) Zero Solution: (d) Because in uniform circular motion work done by the centripetal force is always zero. Problem 123. A particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle about the axis of the circle, the kinetic energy of the particle is given by [CPMT 1995] (a) \[{{L}^{2}}/m{{r}^{2}}\] (b) \[{{L}^{2}}/2m{{r}^{2}}\] (c) \[2{{L}^{2}}/m{{r}^{2}}\] (d) \[m{{r}^{2}}L\] Solution: (b) Rotational kinetic energy \[E=\frac{{{L}^{2}}}{2I}=\frac{{{L}^{2}}}{2m\,{{r}^{2}}}\] (As for a particle \[I=m\,{{r}^{2}}\])
Also \[W=\overrightarrow{F}\,.\,\overrightarrow{S}=\text{ }F\,.\,S\,cos\,\theta \] \[=\,\, F\,.\,S cos{{90}^{o}}=\text{ }0\] Example: (i) When an electron revolve around the nucleus in hydrogen atom in a particular orbit, it neither absorb nor emit any energy means its energy remains constant. (ii) When a satellite established once in a orbit around the earth and it starts revolving with particular speed, then no fuel is required for its circular motion. Sample problem based on work done Problem 121. A particle does uniform circular motion in a horizontal plane. The radius of the circle is 20 cm. The centripetal force acting on the particle is 10 N. It?s kinetic energy is (a) 0.1 Joule (b) 0.2 Joule (c) 2.0 Joule (d) 1.0 Joule Solution: (d) \[\frac{m\,{{v}^{2}}}{r}=10\,N\] (given) \[\Rightarrow m\,{{v}^{2}}=10\times r=10\times 0.2=2\] Kinetic energy \[\frac{1}{2}m\,{{v}^{2}}=\frac{1}{2}(2)=1\,Joule.\] Problem 122. A body of mass 100 g is rotating in a circular path of radius r with constant velocity. The work done in one complete revolution is [AFMC 1998] (a) 100r Joule (b) (r/100) Joule (c) (100/r) Joule (d) Zero Solution: (d) Because in uniform circular motion work done by the centripetal force is always zero. Problem 123. A particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle about the axis of the circle, the kinetic energy of the particle is given by [CPMT 1995] (a) \[{{L}^{2}}/m{{r}^{2}}\] (b) \[{{L}^{2}}/2m{{r}^{2}}\] (c) \[2{{L}^{2}}/m{{r}^{2}}\] (d) \[m{{r}^{2}}L\] Solution: (b) Rotational kinetic energy \[E=\frac{{{L}^{2}}}{2I}=\frac{{{L}^{2}}}{2m\,{{r}^{2}}}\] (As for a particle \[I=m\,{{r}^{2}}\])
You need to login to perform this action.
You will be redirected in
3 sec
