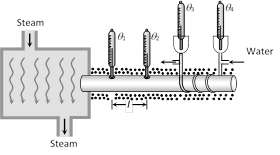
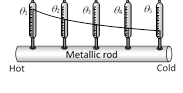
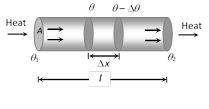
 (1) In this experiment a temperature difference \[({{\theta }_{1}}-{{\theta }_{2}})\] is maintained across a rod of length l and area of cross section A. If the thermal conductivity of the material of the rod is K, then the amount of heat transmitted by the rod from the hot end to the cold end in time t is given by, \[Q=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\] ......(i)
(2) In Searle's experiment, this heat reaching the other end is utilized to raise the temperature of certain amount of water flowing through pipes circulating around the other end of the rod. If temperature of the water at the inlet is \[{{\theta }_{3}}\] and at the outlet is \[{{\theta }_{4}}\], then the amount of heat absorbed by water is given by, \[Q=mc({{\theta }_{4}}-{{\theta }_{3}})\] ......(ii)
(3) Where, m is the mass of the water which has absorbed this heat and temperature is raised and c is the specific heat of the water
Equating (i) and (ii), K can be determined i.e., \[K=\frac{mc({{\theta }_{4}}-{{\theta }_{3}})\,l}{A\,({{\theta }_{1}}-{{\theta }_{2}})\,t}\]
(4) In numericals we may have the situation where the amount of heat travelling to the other end may be required to do some other work e.g., it may be required to melt the given amount of ice. In that case equation (i) will have to be equated to mL.
i.e. \[mL=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\]
(1) In this experiment a temperature difference \[({{\theta }_{1}}-{{\theta }_{2}})\] is maintained across a rod of length l and area of cross section A. If the thermal conductivity of the material of the rod is K, then the amount of heat transmitted by the rod from the hot end to the cold end in time t is given by, \[Q=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\] ......(i)
(2) In Searle's experiment, this heat reaching the other end is utilized to raise the temperature of certain amount of water flowing through pipes circulating around the other end of the rod. If temperature of the water at the inlet is \[{{\theta }_{3}}\] and at the outlet is \[{{\theta }_{4}}\], then the amount of heat absorbed by water is given by, \[Q=mc({{\theta }_{4}}-{{\theta }_{3}})\] ......(ii)
(3) Where, m is the mass of the water which has absorbed this heat and temperature is raised and c is the specific heat of the water
Equating (i) and (ii), K can be determined i.e., \[K=\frac{mc({{\theta }_{4}}-{{\theta }_{3}})\,l}{A\,({{\theta }_{1}}-{{\theta }_{2}})\,t}\]
(4) In numericals we may have the situation where the amount of heat travelling to the other end may be required to do some other work e.g., it may be required to melt the given amount of ice. In that case equation (i) will have to be equated to mL.
i.e. \[mL=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\] 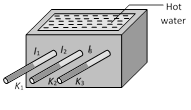 \[\Rightarrow \] Thermal conductivity \[(K)\propto {{(\text{Melted length }l)}^{2}}\]
\[\Rightarrow \] Thermal conductivity \[(K)\propto {{(\text{Melted length }l)}^{2}}\] 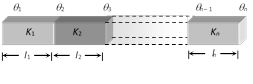 (i) Heat current : Heat current is the same in all the conductors.i.e., \[\frac{Q}{t}={{H}_{1}}={{H}_{2}}={{H}_{3}}.........={{H}_{n}}\]
\[\frac{{{K}_{1}}A({{\theta }_{1}}-{{\theta }_{2}})}{{{l}_{1}}}=\frac{{{K}_{2}}A({{\theta }_{2}}-{{\theta }_{3}})}{{{l}_{2}}}\]\[=\frac{{{K}_{n}}A({{\theta }_{n-1}}-{{\theta }_{n}})}{{{l}_{n}}}\]
(ii) Equivalent thermal resistance : \[R={{R}_{1}}+{{R}_{2}}+.....{{R}_{n}}\]
(iii) Equivalent thermal conductivity : It can be calculated as follows
From \[{{R}_{S}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+...\]
\[\frac{{{l}_{1}}+{{l}_{2}}+...{{l}_{n}}}{{{K}_{s}}}=\frac{{{l}_{1}}}{{{K}_{1}}A}+\frac{{{l}_{2}}}{{{K}_{2}}A}+....+\frac{{{l}_{n}}}{{{K}_{n}}A}\]
\[\Rightarrow \] \[{{K}_{s}}=\frac{{{l}_{1}}+{{l}_{2}}+......\,{{l}_{n}}}{\frac{{{l}_{1}}}{{{K}_{1}}}+\frac{{{l}_{2}}}{{{K}_{2}}}+........\frac{{{l}_{n}}}{{{K}_{n}}}}\]
(a) For n slabs of equal length \[{{K}_{s}}=\frac{n}{\frac{1}{{{K}_{1}}}+\frac{1}{{{K}_{2}}}+\frac{1}{{{K}_{3}}}+.....\frac{1}{{{K}_{n}}}}\]
(b) For two slabs of equal length, \[{{K}_{s}}=\frac{2{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}}\]
(iv) Temperature of interface of composite bar : Let the two bars are arranged in series as shown in the figure.
(i) Heat current : Heat current is the same in all the conductors.i.e., \[\frac{Q}{t}={{H}_{1}}={{H}_{2}}={{H}_{3}}.........={{H}_{n}}\]
\[\frac{{{K}_{1}}A({{\theta }_{1}}-{{\theta }_{2}})}{{{l}_{1}}}=\frac{{{K}_{2}}A({{\theta }_{2}}-{{\theta }_{3}})}{{{l}_{2}}}\]\[=\frac{{{K}_{n}}A({{\theta }_{n-1}}-{{\theta }_{n}})}{{{l}_{n}}}\]
(ii) Equivalent thermal resistance : \[R={{R}_{1}}+{{R}_{2}}+.....{{R}_{n}}\]
(iii) Equivalent thermal conductivity : It can be calculated as follows
From \[{{R}_{S}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+...\]
\[\frac{{{l}_{1}}+{{l}_{2}}+...{{l}_{n}}}{{{K}_{s}}}=\frac{{{l}_{1}}}{{{K}_{1}}A}+\frac{{{l}_{2}}}{{{K}_{2}}A}+....+\frac{{{l}_{n}}}{{{K}_{n}}A}\]
\[\Rightarrow \] \[{{K}_{s}}=\frac{{{l}_{1}}+{{l}_{2}}+......\,{{l}_{n}}}{\frac{{{l}_{1}}}{{{K}_{1}}}+\frac{{{l}_{2}}}{{{K}_{2}}}+........\frac{{{l}_{n}}}{{{K}_{n}}}}\]
(a) For n slabs of equal length \[{{K}_{s}}=\frac{n}{\frac{1}{{{K}_{1}}}+\frac{1}{{{K}_{2}}}+\frac{1}{{{K}_{3}}}+.....\frac{1}{{{K}_{n}}}}\]
(b) For two slabs of equal length, \[{{K}_{s}}=\frac{2{{K}_{1}}{{K}_{2}}}{{{K}_{1}}+{{K}_{2}}}\]
(iv) Temperature of interface of composite bar : Let the two bars are arranged in series as shown in the figure.
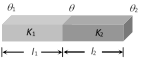 Then heat current is same in the two conductors.
i.e., \[\frac{Q}{t}=\frac{{{K}_{1}}A({{\theta }_{1}}-\theta )}{{{l}_{1}}}=\frac{{{K}_{2}}A(\theta -{{\theta }_{2}})}{{{l}_{2}}}\]
By solving we get \[\theta =\frac{\frac{{{K}_{1}}}{{{l}_{1}}}{{\theta }_{1}}+\frac{{{K}_{2}}}{{{l}_{2}}}{{\theta }_{2}}}{\frac{{{K}_{1}}}{{{l}_{1}}}+\frac{{{K}_{2}}}{{{l}_{2}}}}\]
(a) If \[{{l}_{1}}={{l}_{2}}\] then \[\theta =\frac{{{K}_{1}}{{\theta }_{1}}+{{K}_{2}}{{\theta }_{2}}}{{{K}_{1}}+{{K}_{2}}}\]
(b) If \[{{K}_{1}}={{K}_{2}}\] and \[{{l}_{1}}={{l}_{2}}\] then \[\theta =\frac{{{\theta }_{1}}+{{\theta }_{2}}}{2}\]
(2) Parallel Combination : Let n slabs each of length l, areas \[{{A}_{1}},{{A}_{2}},{{A}_{3}},.....{{A}_{n}}\] and thermal conductivities \[{{K}_{1}},{{K}_{2}},{{K}_{3}},.....{{K}_{n}}\] are connected in parallel then
Then heat current is same in the two conductors.
i.e., \[\frac{Q}{t}=\frac{{{K}_{1}}A({{\theta }_{1}}-\theta )}{{{l}_{1}}}=\frac{{{K}_{2}}A(\theta -{{\theta }_{2}})}{{{l}_{2}}}\]
By solving we get \[\theta =\frac{\frac{{{K}_{1}}}{{{l}_{1}}}{{\theta }_{1}}+\frac{{{K}_{2}}}{{{l}_{2}}}{{\theta }_{2}}}{\frac{{{K}_{1}}}{{{l}_{1}}}+\frac{{{K}_{2}}}{{{l}_{2}}}}\]
(a) If \[{{l}_{1}}={{l}_{2}}\] then \[\theta =\frac{{{K}_{1}}{{\theta }_{1}}+{{K}_{2}}{{\theta }_{2}}}{{{K}_{1}}+{{K}_{2}}}\]
(b) If \[{{K}_{1}}={{K}_{2}}\] and \[{{l}_{1}}={{l}_{2}}\] then \[\theta =\frac{{{\theta }_{1}}+{{\theta }_{2}}}{2}\]
(2) Parallel Combination : Let n slabs each of length l, areas \[{{A}_{1}},{{A}_{2}},{{A}_{3}},.....{{A}_{n}}\] and thermal conductivities \[{{K}_{1}},{{K}_{2}},{{K}_{3}},.....{{K}_{n}}\] are connected in parallel then
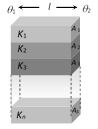 (i) Equivalent resistance : \[\frac{1}{{{R}_{s}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}+.....\frac{1}{{{R}_{n}}}\]
For two slabs \[{{R}_{s}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\]
(ii) Temperature gradient : Same across each slab. (iii) Heat current : in each slab will be different. Net heat current will be the sum of heat currents through individual slabs. i.e., \[H={{H}_{1}}+{{H}_{2}}+{{H}_{3}}+....{{H}_{n}}\] \[\frac{K({{A}_{1}}+{{A}_{2}}+.....+{{A}_{n}})\,({{\theta }_{1}}-{{\theta }_{2}})}{l}\]
\[=\frac{{{K}_{1}}{{A}_{1}}({{\theta }_{1}}-{{\theta }_{2}})}{l}+\frac{{{K}_{2}}{{A}_{2}}({{\theta }_{1}}-{{\theta }_{2}})}{l}+...+\frac{{{K}_{n}}{{A}_{n}}\,({{\theta }_{1}}-{{\theta }_{2}})}{l}\]
\[\Rightarrow \] \[K=\frac{{{K}_{1}}{{A}_{1}}+{{K}_{2}}{{A}_{2}}+{{K}_{3}}{{A}_{3}}+.....{{K}_{n}}{{A}_{n}}}{{{A}_{1}}+{{A}_{2}}+{{A}_{3}}+.....{{A}_{n}}}\]
(a) For n slabs of equal area \[K=\frac{{{K}_{1}}+{{K}_{2}}+{{K}_{3}}+.....{{K}_{n}}}{n}\]
(b) For two slabs of equal area \[K=\frac{{{K}_{1}}+{{K}_{2}}}{2}\].
(i) Equivalent resistance : \[\frac{1}{{{R}_{s}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}+.....\frac{1}{{{R}_{n}}}\]
For two slabs \[{{R}_{s}}=\frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}\]
(ii) Temperature gradient : Same across each slab. (iii) Heat current : in each slab will be different. Net heat current will be the sum of heat currents through individual slabs. i.e., \[H={{H}_{1}}+{{H}_{2}}+{{H}_{3}}+....{{H}_{n}}\] \[\frac{K({{A}_{1}}+{{A}_{2}}+.....+{{A}_{n}})\,({{\theta }_{1}}-{{\theta }_{2}})}{l}\]
\[=\frac{{{K}_{1}}{{A}_{1}}({{\theta }_{1}}-{{\theta }_{2}})}{l}+\frac{{{K}_{2}}{{A}_{2}}({{\theta }_{1}}-{{\theta }_{2}})}{l}+...+\frac{{{K}_{n}}{{A}_{n}}\,({{\theta }_{1}}-{{\theta }_{2}})}{l}\]
\[\Rightarrow \] \[K=\frac{{{K}_{1}}{{A}_{1}}+{{K}_{2}}{{A}_{2}}+{{K}_{3}}{{A}_{3}}+.....{{K}_{n}}{{A}_{n}}}{{{A}_{1}}+{{A}_{2}}+{{A}_{3}}+.....{{A}_{n}}}\]
(a) For n slabs of equal area \[K=\frac{{{K}_{1}}+{{K}_{2}}+{{K}_{3}}+.....{{K}_{n}}}{n}\]
(b) For two slabs of equal area \[K=\frac{{{K}_{1}}+{{K}_{2}}}{2}\].
 (2) We feel warmer in a fur coat. The air enclosed in the fur coat being bad conductor heat does not allow the body heat to flow outside. Hence we feel warmer in a fur coat.
(3) Eskimos make double walled houses of the blocks of ice. Air enclosed in between the double walls prevents transmission of heat from the house to the cold surroundings.
(2) We feel warmer in a fur coat. The air enclosed in the fur coat being bad conductor heat does not allow the body heat to flow outside. Hence we feel warmer in a fur coat.
(3) Eskimos make double walled houses of the blocks of ice. Air enclosed in between the double walls prevents transmission of heat from the house to the cold surroundings.
 For exactly the same reason, two thin blankets are warmer than one blanket of their combined thickness. The layer of air enclosed in between the two blankets makes the difference.
(4) Wire gauze is placed over the flame of Bunsen burner while heating the flask or a beaker so that the flame does not go beyond the gauze and hence there is no direct contact between the flame and the flask. The wire gauze being a good conductor of heat, absorb the heat of the flame and transmit it to the flask.
For exactly the same reason, two thin blankets are warmer than one blanket of their combined thickness. The layer of air enclosed in between the two blankets makes the difference.
(4) Wire gauze is placed over the flame of Bunsen burner while heating the flask or a beaker so that the flame does not go beyond the gauze and hence there is no direct contact between the flame and the flask. The wire gauze being a good conductor of heat, absorb the heat of the flame and transmit it to the flask.
 Davy's safety lamp has been designed on this principle. The gases in the mines burn inside the gauze placed around the flame of the lamp. The temperature outside the gauze is not high, so the gases outside the gauze do not catch fire.
(5) Birds often swell their feathers in winter. By doing so, they enclose more air between their bodies and the feathers. The air, being bad conductor of heat prevents the out flow of their body heat. Thus, birds feel warmer in winter by swelling their feathers.
Davy's safety lamp has been designed on this principle. The gases in the mines burn inside the gauze placed around the flame of the lamp. The temperature outside the gauze is not high, so the gases outside the gauze do not catch fire.
(5) Birds often swell their feathers in winter. By doing so, they enclose more air between their bodies and the feathers. The air, being bad conductor of heat prevents the out flow of their body heat. Thus, birds feel warmer in winter by swelling their feathers. 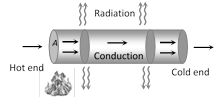 (1) Variable state : In this state Temperature of every part of the rod increases.
Heat received by each cross-section of the rod from hotter end used in three ways.
(i) A part increases temperature of itself.
(ii) Another part transferred to neighbouring cross-section.
(iii) Remaining part radiates.
(1) Variable state : In this state Temperature of every part of the rod increases.
Heat received by each cross-section of the rod from hotter end used in three ways.
(i) A part increases temperature of itself.
(ii) Another part transferred to neighbouring cross-section.
(iii) Remaining part radiates.
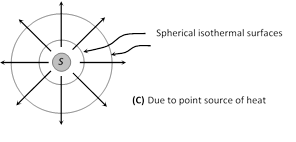 (4) Temperature gradient (T.G.) : The rate of change of temperature with distance between two isothermal surfaces is called temperature gradient. Hence
(4) Temperature gradient (T.G.) : The rate of change of temperature with distance between two isothermal surfaces is called temperature gradient. Hence
 (i) Temperature gradient \[=\frac{-\Delta \theta }{\Delta x}\]
(ii) The negative sign show that temperature \[\theta \] decreases as the distance x increases in the direction of heat flow.
(iii) For uniform temperature fall \[\frac{{{\theta }_{1}}-{{\theta }_{2}}}{l}=\frac{\Delta \theta }{\Delta x}\]
(iv) Unit : K/m or \[^{o}C/m\] (S.I.) and Dimensions \[[{{L}^{-1}}\theta ]\]
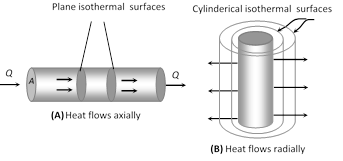
(5) Law of thermal conductivity : Consider a rod of length l and area of cross-section A whose faces are maintained at temperature \[{{\theta }_{1}}\] and \[{{\theta }_{2}}\] respectively. The curved surface of rod is kept insulated from surrounding to avoid leakage of heat
(i) Temperature gradient \[=\frac{-\Delta \theta }{\Delta x}\]
(ii) The negative sign show that temperature \[\theta \] decreases as the distance x increases in the direction of heat flow.
(iii) For uniform temperature fall \[\frac{{{\theta }_{1}}-{{\theta }_{2}}}{l}=\frac{\Delta \theta }{\Delta x}\]
(iv) Unit : K/m or \[^{o}C/m\] (S.I.) and Dimensions \[[{{L}^{-1}}\theta ]\]
(5) Law of thermal conductivity : Consider a rod of length l and area of cross-section A whose faces are maintained at temperature \[{{\theta }_{1}}\] and \[{{\theta }_{2}}\] respectively. The curved surface of rod is kept insulated from surrounding to avoid leakage of heat
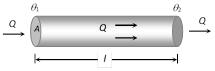 (i) In steady state the amount of heat flowing from one face to the other face in time t is given by \[Q=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\]
where K is coefficient of thermal conductivity of material of rod.
(ii) Rate of flow of heat i.e. heat current \[\frac{Q}{t}=H\]\[=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,}{l}\]
(iii) In case of non-steady state or variable cross-section, a more general equation can be used to solve problems.
\[\frac{dQ}{dt}=-\,KA\frac{d\theta }{dx}\]
(6) More about K : It is the measure of the ability of a substance to conduct heat through it.
(i) Units : Cal/cm-sec \[^{o}C\] (in C.G.S.), kcal/m-sec-K (in M.K.S.) and W/m- K (in S.I.). Dimension : \[[ML{{T}^{-3}}{{\theta }^{-1}}]\]
(ii) The magnitude of K depends only on nature of the material.
(iii) Substances in which heat flows quickly and easily are known as good conductor of heat. They possesses large thermal conductivity due to large number of free more...
(i) In steady state the amount of heat flowing from one face to the other face in time t is given by \[Q=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,t}{l}\]
where K is coefficient of thermal conductivity of material of rod.
(ii) Rate of flow of heat i.e. heat current \[\frac{Q}{t}=H\]\[=\frac{KA({{\theta }_{1}}-{{\theta }_{2}})\,}{l}\]
(iii) In case of non-steady state or variable cross-section, a more general equation can be used to solve problems.
\[\frac{dQ}{dt}=-\,KA\frac{d\theta }{dx}\]
(6) More about K : It is the measure of the ability of a substance to conduct heat through it.
(i) Units : Cal/cm-sec \[^{o}C\] (in C.G.S.), kcal/m-sec-K (in M.K.S.) and W/m- K (in S.I.). Dimension : \[[ML{{T}^{-3}}{{\theta }^{-1}}]\]
(ii) The magnitude of K depends only on nature of the material.
(iii) Substances in which heat flows quickly and easily are known as good conductor of heat. They possesses large thermal conductivity due to large number of free more...  (1) Heat flows from hot end to cold end. Particles of the medium simply oscillate but do not leave their place.
(2) Medium is necessary for conduction
(3) It is a slow process
(4) The temperature of the medium increases through which heat flows
(5) Conduction is a process which is possible in all states of matter.
(6) When liquid and gases are heated from the top, they conduct heat from top to bottom.
(7) In solids only conduction takes place
(8) In non-metallic solids and fluids the conduction takes place only due to vibrations of molecules, therefore they are poor conductors.
(9) In metallic solids free electrons carry the heat energy, therefore they are good conductor of heat.
(1) Heat flows from hot end to cold end. Particles of the medium simply oscillate but do not leave their place.
(2) Medium is necessary for conduction
(3) It is a slow process
(4) The temperature of the medium increases through which heat flows
(5) Conduction is a process which is possible in all states of matter.
(6) When liquid and gases are heated from the top, they conduct heat from top to bottom.
(7) In solids only conduction takes place
(8) In non-metallic solids and fluids the conduction takes place only due to vibrations of molecules, therefore they are poor conductors.
(9) In metallic solids free electrons carry the heat energy, therefore they are good conductor of heat. 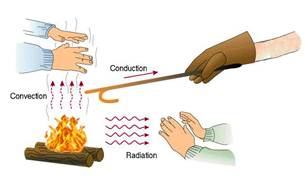
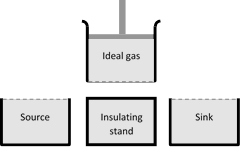 It consists of the following parts
(i) A cylinder with perfectly non-conducting walls and a perfectly conducting base containing a perfect gas as working substance and fitted with a non-conducting frictionless piston
(ii) A source of infinite thermal capacity maintained at constant higher temperature \[{{T}_{1}}\].
(iii) A sink of infinite thermal capacity maintained at constant lower temperature \[{{T}_{2}}\].
(iv) A perfectly non-conducting stand for the cylinder.
(2) Carnot cycle : As the engine works, the working substance of the engine undergoes a cycle known as Carnot cycle. The Carnot cycle consists of the following four strokes
It consists of the following parts
(i) A cylinder with perfectly non-conducting walls and a perfectly conducting base containing a perfect gas as working substance and fitted with a non-conducting frictionless piston
(ii) A source of infinite thermal capacity maintained at constant higher temperature \[{{T}_{1}}\].
(iii) A sink of infinite thermal capacity maintained at constant lower temperature \[{{T}_{2}}\].
(iv) A perfectly non-conducting stand for the cylinder.
(2) Carnot cycle : As the engine works, the working substance of the engine undergoes a cycle known as Carnot cycle. The Carnot cycle consists of the following four strokes
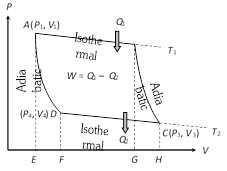 (i) First stroke (Isothermal expansion) (curve AB) :
The cylinder containing ideal gas as working substance allowed to expand slowly at this constant temperature \[{{T}_{1}}\].
Work done = Heat absorbed by the system
\[{{W}_{1}}={{Q}_{1}}=\int_{\,{{V}_{1}}}^{\,{{V}_{2}}}{P\,dV}=R{{T}_{1}}{{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)=\]Area ABGE
(ii) Second stroke (Adiabatic expansion) (curve BC) :
The cylinder is then placed on the non conducting stand and the gas is allowed to expand adiabatically till the temperature falls from \[{{T}_{1}}\] to \[{{T}_{2}}\].
\[{{W}_{2}}=\int_{\,{{V}_{2}}}^{\,{{V}_{3}}}{P\,dV}=\frac{R}{(\gamma -1)}[{{T}_{1}}-{{T}_{2}}]=\]Area BCHG
(iii) Third stroke (Isothermal compression) (curve CD) :
The cylinder is placed on the sink and the gas is compressed at constant temperature \[{{T}_{2}}\].
Work done = Heat released by the system
\[{{W}_{3}}={{Q}_{2}}=-\int_{\,{{V}_{3}}}^{\,{{V}_{4}}}{\,P\,dV}=-R{{T}_{2}}{{\log }_{e}}\frac{{{V}_{4}}}{{{V}_{3}}}\]
\[=R{{T}_{2}}{{\log }_{e}}\frac{{{V}_{3}}}{{{V}_{4}}}=\text{Area }CDFH\,\]
(iv) Fourth stroke (adiabatic compression) (curve DA) : Finally the cylinder is again placed on non-conducting stand and the compression is continued so that gas returns to its initial stage.
\[{{W}_{4}}=-\int_{\,{{V}_{4}}}^{\,{{V}_{1}}}{P\,dV}=-\frac{R}{\gamma -1}({{T}_{2}}-{{T}_{1}})\]\[=\frac{R}{\gamma -1}({{T}_{1}}-{{T}_{2}})=\text{Area }ADFE\]
(3) Efficiency of Carnot cycle : The efficiency of engine is defined as the ratio of work done to the heat supplied i.e.
\[\eta =\frac{\text{Work done}}{\text{Heat input}}=\frac{W}{{{Q}_{1}}}\]
Net work done during the complete cycle
\[W={{W}_{1}}+{{W}_{2}}+(-{{W}_{3}})+(-{{W}_{4}})\]\[={{W}_{1}}-{{W}_{3}}=\text{Area }ABCD\] [As \[{{W}_{2}}={{W}_{4}}\]]
\[\therefore \] \[\eta =\frac{W}{{{Q}_{1}}}=\frac{{{W}_{1}}-{{W}_{3}}}{{{W}_{1}}}=\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{W}_{3}}}{{{W}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
or \[\eta =1-\frac{R{{T}_{2}}{{\log }_{e}}({{V}_{3}}/{{V}_{4}})}{R{{T}_{1}}{{\log }_{e}}({{V}_{2}}/{{V}_{1}})}\]
Since points B and C lie on same adiabatic curve
\[\therefore \] \[{{T}_{1}}V_{2}^{\gamma -1}={{T}_{2}}V_{3}^{\gamma -1}\] or \[\frac{{{T}_{1}}}{{{T}_{2}}}={{\left( \frac{{{V}_{3}}}{{{V}_{2}}} \right)}^{\gamma -1}}\] ...(i)
Also point D and A lie on the same adiabatic curve
\[\therefore \] \[{{T}_{1}}V_{1}^{\gamma -1}={{T}_{2}}V_{4}^{\gamma -1}\] or \[\frac{{{T}_{1}}}{{{T}_{2}}}={{\left( \frac{{{V}_{4}}}{{{V}_{1}}} \right)}^{\gamma -1}}\] ...(ii)
From (i) and (ii), \[\frac{{{V}_{3}}}{{{V}_{2}}}=\frac{{{V}_{4}}}{{{V}_{1}}}\] or \[\frac{{{V}_{3}}}{{{V}_{4}}}=\frac{{{V}_{2}}}{{{V}_{1}}}\]\[\Rightarrow \]\[{{\log }_{e}}\left( \frac{{{V}_{3}}}{{{V}_{4}}} \right)={{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\]
So efficiency of Carnot engine \[\eta =1-\frac{{{T}_{2}}}{{{T}_{1}}}\]
(i) Efficiency of a heat engine depends only on temperatures of source and sink and is independent of all other factors.
(ii) All reversible heat engines working between same temperatures are equally efficient and no heat engine can be more efficient than Carnot engine (as it is ideal).
(iii) As on Kelvin scale, temperature can never be negative (as 0 K is more...
(i) First stroke (Isothermal expansion) (curve AB) :
The cylinder containing ideal gas as working substance allowed to expand slowly at this constant temperature \[{{T}_{1}}\].
Work done = Heat absorbed by the system
\[{{W}_{1}}={{Q}_{1}}=\int_{\,{{V}_{1}}}^{\,{{V}_{2}}}{P\,dV}=R{{T}_{1}}{{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)=\]Area ABGE
(ii) Second stroke (Adiabatic expansion) (curve BC) :
The cylinder is then placed on the non conducting stand and the gas is allowed to expand adiabatically till the temperature falls from \[{{T}_{1}}\] to \[{{T}_{2}}\].
\[{{W}_{2}}=\int_{\,{{V}_{2}}}^{\,{{V}_{3}}}{P\,dV}=\frac{R}{(\gamma -1)}[{{T}_{1}}-{{T}_{2}}]=\]Area BCHG
(iii) Third stroke (Isothermal compression) (curve CD) :
The cylinder is placed on the sink and the gas is compressed at constant temperature \[{{T}_{2}}\].
Work done = Heat released by the system
\[{{W}_{3}}={{Q}_{2}}=-\int_{\,{{V}_{3}}}^{\,{{V}_{4}}}{\,P\,dV}=-R{{T}_{2}}{{\log }_{e}}\frac{{{V}_{4}}}{{{V}_{3}}}\]
\[=R{{T}_{2}}{{\log }_{e}}\frac{{{V}_{3}}}{{{V}_{4}}}=\text{Area }CDFH\,\]
(iv) Fourth stroke (adiabatic compression) (curve DA) : Finally the cylinder is again placed on non-conducting stand and the compression is continued so that gas returns to its initial stage.
\[{{W}_{4}}=-\int_{\,{{V}_{4}}}^{\,{{V}_{1}}}{P\,dV}=-\frac{R}{\gamma -1}({{T}_{2}}-{{T}_{1}})\]\[=\frac{R}{\gamma -1}({{T}_{1}}-{{T}_{2}})=\text{Area }ADFE\]
(3) Efficiency of Carnot cycle : The efficiency of engine is defined as the ratio of work done to the heat supplied i.e.
\[\eta =\frac{\text{Work done}}{\text{Heat input}}=\frac{W}{{{Q}_{1}}}\]
Net work done during the complete cycle
\[W={{W}_{1}}+{{W}_{2}}+(-{{W}_{3}})+(-{{W}_{4}})\]\[={{W}_{1}}-{{W}_{3}}=\text{Area }ABCD\] [As \[{{W}_{2}}={{W}_{4}}\]]
\[\therefore \] \[\eta =\frac{W}{{{Q}_{1}}}=\frac{{{W}_{1}}-{{W}_{3}}}{{{W}_{1}}}=\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{W}_{3}}}{{{W}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
or \[\eta =1-\frac{R{{T}_{2}}{{\log }_{e}}({{V}_{3}}/{{V}_{4}})}{R{{T}_{1}}{{\log }_{e}}({{V}_{2}}/{{V}_{1}})}\]
Since points B and C lie on same adiabatic curve
\[\therefore \] \[{{T}_{1}}V_{2}^{\gamma -1}={{T}_{2}}V_{3}^{\gamma -1}\] or \[\frac{{{T}_{1}}}{{{T}_{2}}}={{\left( \frac{{{V}_{3}}}{{{V}_{2}}} \right)}^{\gamma -1}}\] ...(i)
Also point D and A lie on the same adiabatic curve
\[\therefore \] \[{{T}_{1}}V_{1}^{\gamma -1}={{T}_{2}}V_{4}^{\gamma -1}\] or \[\frac{{{T}_{1}}}{{{T}_{2}}}={{\left( \frac{{{V}_{4}}}{{{V}_{1}}} \right)}^{\gamma -1}}\] ...(ii)
From (i) and (ii), \[\frac{{{V}_{3}}}{{{V}_{2}}}=\frac{{{V}_{4}}}{{{V}_{1}}}\] or \[\frac{{{V}_{3}}}{{{V}_{4}}}=\frac{{{V}_{2}}}{{{V}_{1}}}\]\[\Rightarrow \]\[{{\log }_{e}}\left( \frac{{{V}_{3}}}{{{V}_{4}}} \right)={{\log }_{e}}\left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)\]
So efficiency of Carnot engine \[\eta =1-\frac{{{T}_{2}}}{{{T}_{1}}}\]
(i) Efficiency of a heat engine depends only on temperatures of source and sink and is independent of all other factors.
(ii) All reversible heat engines working between same temperatures are equally efficient and no heat engine can be more efficient than Carnot engine (as it is ideal).
(iii) As on Kelvin scale, temperature can never be negative (as 0 K is more... You need to login to perform this action.
You will be redirected in
3 sec
