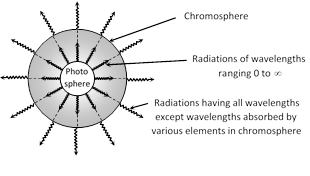
 (iv) During total solar eclipse these lines appear bright because the gases and vapour present in the chromosphere start emitting those radiation which they had absorbed.
(iv) During total solar eclipse these lines appear bright because the gases and vapour present in the chromosphere start emitting those radiation which they had absorbed. 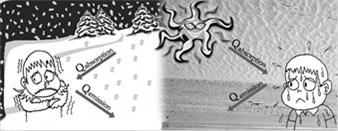 (1) Every body emits heat radiations at all finite temperature (Except 0 K) as well as it absorbs radiations from the surroundings.
(2) Exchange of energy along various bodies takes place via radiation.
(3) The process of heat exchange among various bodies is a continuous phenomenon.
(4) At absolute zero temperature \[(0\,\,K\,\,\text{or}\,\,-{{273}^{o}}C)\] this law is not applicable because at this temperature the heat exchange among various bodies ceases.
(5) If \[{{Q}_{emission}}>{{Q}_{absorbed}}\to \] temperature of body decreases and consequently the body appears colder.
If \[{{Q}_{emission}}
(1) Every body emits heat radiations at all finite temperature (Except 0 K) as well as it absorbs radiations from the surroundings.
(2) Exchange of energy along various bodies takes place via radiation.
(3) The process of heat exchange among various bodies is a continuous phenomenon.
(4) At absolute zero temperature \[(0\,\,K\,\,\text{or}\,\,-{{273}^{o}}C)\] this law is not applicable because at this temperature the heat exchange among various bodies ceases.
(5) If \[{{Q}_{emission}}>{{Q}_{absorbed}}\to \] temperature of body decreases and consequently the body appears colder.
If \[{{Q}_{emission}}  (6) A perfectly black body can not be realised in practice but materials like Platinum black or Lamp black come close to being ideal black bodies. Such materials absorbs 96% to 85% of the incident radiations.
(6) A perfectly black body can not be realised in practice but materials like Platinum black or Lamp black come close to being ideal black bodies. Such materials absorbs 96% to 85% of the incident radiations. 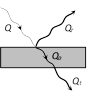 (1) \[Q={{Q}_{a}}+{{Q}_{r}}+{{Q}_{t}}\]
(2) \[\frac{{{Q}_{a}}}{Q}+\frac{{{Q}_{r}}}{Q}+\frac{{{Q}_{t}}}{Q}=a+r+t=1\]
(3) \[a=\frac{{{Q}_{a}}}{Q}\]= Absorptance or absorbing power
\[r=\frac{{{Q}_{r}}}{Q}\] = Reflectance or reflecting power
\[t=\frac{{{Q}_{t}}}{Q}\]= Transmittance or transmitting power
(4) r, a and t all are the pure ratios so they have no unit and dimension.
(5) Different bodies
(i) If \[a=t=0\] and \[r=1\to \] body is perfect reflector
(ii) If \[r=t=0\] and \[a=1\to \] body is perfectly black body
(iii) If, \[a=r=0\] and \[t=1\to \] body is perfect transmitter
(iv) If \[t=0\Rightarrow r+a=1\,\,\text{or}\,\,a=1-r\] i.e. good reflectors are bad absorbers.
(1) \[Q={{Q}_{a}}+{{Q}_{r}}+{{Q}_{t}}\]
(2) \[\frac{{{Q}_{a}}}{Q}+\frac{{{Q}_{r}}}{Q}+\frac{{{Q}_{t}}}{Q}=a+r+t=1\]
(3) \[a=\frac{{{Q}_{a}}}{Q}\]= Absorptance or absorbing power
\[r=\frac{{{Q}_{r}}}{Q}\] = Reflectance or reflecting power
\[t=\frac{{{Q}_{t}}}{Q}\]= Transmittance or transmitting power
(4) r, a and t all are the pure ratios so they have no unit and dimension.
(5) Different bodies
(i) If \[a=t=0\] and \[r=1\to \] body is perfect reflector
(ii) If \[r=t=0\] and \[a=1\to \] body is perfectly black body
(iii) If, \[a=r=0\] and \[t=1\to \] body is perfect transmitter
(iv) If \[t=0\Rightarrow r+a=1\,\,\text{or}\,\,a=1-r\] i.e. good reflectors are bad absorbers. | Temperature | Colour |
| \[{{525}^{o}}C\] | Dull red |
| \[{{900}^{o}}C\] | Cherry red |
| \[{{1100}^{o}}C\] | Orange red |
| \[{{1200}^{o}}C\] | Yellow |
| \[{{1600}^{o}}C\] | White |
 (2) Precisely it is electromagnetic energy transfer in the form of electromagnetic wave through any medium. It is possible even in vacuum e.g. the heat from the sun reaches the earth through radiation.
(3) The wavelength of thermal radiations ranges from \[7.8\times {{10}^{-7}}\,m\] to \[4\times {{10}^{-4}}\,m\]. They belong to infra-red region of the electromagnetic spectrum. That is why thermal radiations are also called infra-red radiations.
(4) Medium is not required for the propagation of these radiations.
(5) They produce sensation of warmth in us but we can't see them.
(6) Every body whose temperature is above zero Kelvin emits thermal radiation.
(7) Their speed is equal to that of light i.e. \[(=3\times {{10}^{8}}\,m/s)\].
(8) Their intensity is inversely proportional to the square of distance of point of observation from the source (i.e. \[I\propto 1/{{d}^{2}}\]).
(9) Just as light waves, they follow laws of reflection, refraction, interference, diffraction and polarisation.
(10) When these radiations fall on a surface then exert pressure on that surface which is known as radiation pressure.
(11) While travelling these radiations travel just like photons of other electromagnetic waves. They manifest themselves as heat only when they are absorbed by a substance.
(12) Spectrum of these radiations can not be obtained with the help of glass prism because it absorbs heat radiations. It is obtained by quartz or rock salt prism because these materials do not have free electrons and interatomic vibrational frequency is greater than the radiation frequency, hence they do not absorb heat radiations.
(13) Diathermanous Medium : A medium which allows heat radiations to pass through it without absorbing them is called diathermanous medium. Thus the temperature of a diathermanous medium does not increase irrespective of the amount of the thermal radiations passing through it e.g., dry air, \[S{{O}_{2}}\], rock salt \[(NaCl)\].
(i) Dry air does not get heated in summers by absorbing heat radiations from sun. It gets heated through convection by receiving heat from the surface of earth.
(ii) In winters heat from sun is directly absorbed by human flesh while the surrounding air being diathermanous is still cool. This is the reason that sun's warmth in winter season appears very satisfying to us.
(14) Athermanous medium : A medium which partly absorbs heat rays is called a thermous medium As a result temperature of an athermanous medium increases when heat radiations pass through it e.g., wood, metal, moist air, simple glass, human flesh etc.
(2) Precisely it is electromagnetic energy transfer in the form of electromagnetic wave through any medium. It is possible even in vacuum e.g. the heat from the sun reaches the earth through radiation.
(3) The wavelength of thermal radiations ranges from \[7.8\times {{10}^{-7}}\,m\] to \[4\times {{10}^{-4}}\,m\]. They belong to infra-red region of the electromagnetic spectrum. That is why thermal radiations are also called infra-red radiations.
(4) Medium is not required for the propagation of these radiations.
(5) They produce sensation of warmth in us but we can't see them.
(6) Every body whose temperature is above zero Kelvin emits thermal radiation.
(7) Their speed is equal to that of light i.e. \[(=3\times {{10}^{8}}\,m/s)\].
(8) Their intensity is inversely proportional to the square of distance of point of observation from the source (i.e. \[I\propto 1/{{d}^{2}}\]).
(9) Just as light waves, they follow laws of reflection, refraction, interference, diffraction and polarisation.
(10) When these radiations fall on a surface then exert pressure on that surface which is known as radiation pressure.
(11) While travelling these radiations travel just like photons of other electromagnetic waves. They manifest themselves as heat only when they are absorbed by a substance.
(12) Spectrum of these radiations can not be obtained with the help of glass prism because it absorbs heat radiations. It is obtained by quartz or rock salt prism because these materials do not have free electrons and interatomic vibrational frequency is greater than the radiation frequency, hence they do not absorb heat radiations.
(13) Diathermanous Medium : A medium which allows heat radiations to pass through it without absorbing them is called diathermanous medium. Thus the temperature of a diathermanous medium does not increase irrespective of the amount of the thermal radiations passing through it e.g., dry air, \[S{{O}_{2}}\], rock salt \[(NaCl)\].
(i) Dry air does not get heated in summers by absorbing heat radiations from sun. It gets heated through convection by receiving heat from the surface of earth.
(ii) In winters heat from sun is directly absorbed by human flesh while the surrounding air being diathermanous is still cool. This is the reason that sun's warmth in winter season appears very satisfying to us.
(14) Athermanous medium : A medium which partly absorbs heat rays is called a thermous medium As a result temperature of an athermanous medium increases when heat radiations pass through it e.g., wood, metal, moist air, simple glass, human flesh etc.  Mode of transfer of heat by means of migration of material particles of medium is called convection. It is of two types.
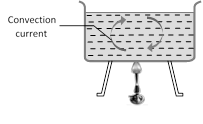
(1) Natural convection : This arise due to difference of densities at two places and is a consequence of gravity because on account of gravity the hot light particles rise up and cold heavy particles try setting down. It mostly occurs on heating a liquid/fluid.
Mode of transfer of heat by means of migration of material particles of medium is called convection. It is of two types.
(1) Natural convection : This arise due to difference of densities at two places and is a consequence of gravity because on account of gravity the hot light particles rise up and cold heavy particles try setting down. It mostly occurs on heating a liquid/fluid.
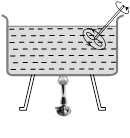
 (2) Forced convection : If a fluid is forced to move to take up heat from a hot body then the convection process is called forced convection. In this case Newton's law of cooling holds good. According to which rate of loss of heat from a hot body due to moving fluid is directly proportional to the surface area of body and excess temperature of body over its surroundings i.e.
(2) Forced convection : If a fluid is forced to move to take up heat from a hot body then the convection process is called forced convection. In this case Newton's law of cooling holds good. According to which rate of loss of heat from a hot body due to moving fluid is directly proportional to the surface area of body and excess temperature of body over its surroundings i.e.
 \[\frac{Q}{t}\propto A(T-{{T}_{0}})\]\[\Rightarrow \] \[\frac{Q}{t}=h\,A(T-{{T}_{0}})\]
where h = Constant of proportionality called convection coefficient, T = Temperature of body and \[{{T}_{0}}=\] Temperature of surrounding
Convection coefficient (h) depends on properties of fluid such as density, viscosity, specific heat and thermal conductivity.
(3) Natural convection takes place from bottom to top while forced convection in any direction.
(4) In case of natural convection, convection currents move warm air upwards and cool air downwards. That is why heating is done from base, while cooling from the top.
(5) Natural convection plays an important role in ventilation, in changing climate and weather and in forming land and sea breezes and trade winds.
(6) Natural convection is not possible in a gravity free region such as a free falling lift or an orbiting satellite.
(7) The force of blood in our body by heart helps in keeping the temperature of body constant.
(8) If liquids and gases are heated from the top (so that convection is not possible) they transfer heat (from top to bottom) by conduction.
(9) Mercury though a liquid is heated by conduction and not by convection.
\[\frac{Q}{t}\propto A(T-{{T}_{0}})\]\[\Rightarrow \] \[\frac{Q}{t}=h\,A(T-{{T}_{0}})\]
where h = Constant of proportionality called convection coefficient, T = Temperature of body and \[{{T}_{0}}=\] Temperature of surrounding
Convection coefficient (h) depends on properties of fluid such as density, viscosity, specific heat and thermal conductivity.
(3) Natural convection takes place from bottom to top while forced convection in any direction.
(4) In case of natural convection, convection currents move warm air upwards and cool air downwards. That is why heating is done from base, while cooling from the top.
(5) Natural convection plays an important role in ventilation, in changing climate and weather and in forming land and sea breezes and trade winds.
(6) Natural convection is not possible in a gravity free region such as a free falling lift or an orbiting satellite.
(7) The force of blood in our body by heart helps in keeping the temperature of body constant.
(8) If liquids and gases are heated from the top (so that convection is not possible) they transfer heat (from top to bottom) by conduction.
(9) Mercury though a liquid is heated by conduction and not by convection.  (5) As \[d{{Q}_{1}}=d{{Q}_{2}}\], hence, rate of growth of ice will be \[(dy/dt)=(K\theta /\rho Ly)\]
So, the time taken by ice to grow to a thickness y is
\[t=\frac{\rho L}{K\theta }\int_{\,0}^{\,y}{\,y\,dy}=\frac{\rho L}{2K\theta }{{y}^{2}}\]
(6) If the thickness is increased from \[{{y}_{1}}\] to \[{{y}_{2}}\] then time taken \[t=\frac{\rho L}{K\theta }\int_{\,{{y}_{1}}}^{\,{{y}_{2}}}{\,ydy}=\frac{\rho L}{2K\theta }(y_{2}^{2}-y_{1}^{2})\]
(7) Take care and do not apply a negative sign for putting values of temperature in formula and also do not convert it to absolute scale.
(8) Ice is a poor conductor of heat, therefore the rate of increase of thickness of ice on ponds decreases with time.
(9) It follows from the above equation that time taken to double and triple the thickness, will be in the ratio of
\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}::{{1}^{2}}:{{2}^{2}}:{{3}^{2}},\] i.e., \[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}::1:4:9\]
(10) The time intervals to change the thickness from 0 to y, from y to 2y and so on will be in the ratio
\[\Delta {{t}_{1}}:\Delta {{t}_{2}}:\Delta {{t}_{3}}::({{1}^{2}}-{{0}^{2}}):({{2}^{2}}-{{1}^{2}}):({{3}^{2}}:{{2}^{2}})\]
\[\Rightarrow \] \[\Delta {{t}_{1}}:\Delta {{t}_{2}}:\Delta {{t}_{3}}::1:3:5\]
(5) As \[d{{Q}_{1}}=d{{Q}_{2}}\], hence, rate of growth of ice will be \[(dy/dt)=(K\theta /\rho Ly)\]
So, the time taken by ice to grow to a thickness y is
\[t=\frac{\rho L}{K\theta }\int_{\,0}^{\,y}{\,y\,dy}=\frac{\rho L}{2K\theta }{{y}^{2}}\]
(6) If the thickness is increased from \[{{y}_{1}}\] to \[{{y}_{2}}\] then time taken \[t=\frac{\rho L}{K\theta }\int_{\,{{y}_{1}}}^{\,{{y}_{2}}}{\,ydy}=\frac{\rho L}{2K\theta }(y_{2}^{2}-y_{1}^{2})\]
(7) Take care and do not apply a negative sign for putting values of temperature in formula and also do not convert it to absolute scale.
(8) Ice is a poor conductor of heat, therefore the rate of increase of thickness of ice on ponds decreases with time.
(9) It follows from the above equation that time taken to double and triple the thickness, will be in the ratio of
\[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}::{{1}^{2}}:{{2}^{2}}:{{3}^{2}},\] i.e., \[{{t}_{1}}:{{t}_{2}}:{{t}_{3}}::1:4:9\]
(10) The time intervals to change the thickness from 0 to y, from y to 2y and so on will be in the ratio
\[\Delta {{t}_{1}}:\Delta {{t}_{2}}:\Delta {{t}_{3}}::({{1}^{2}}-{{0}^{2}}):({{2}^{2}}-{{1}^{2}}):({{3}^{2}}:{{2}^{2}})\]
\[\Rightarrow \] \[\Delta {{t}_{1}}:\Delta {{t}_{2}}:\Delta {{t}_{3}}::1:3:5\] You need to login to perform this action.
You will be redirected in
3 sec
