Linear Equation in Three Variables
We can also use the system of linear equation for solving the linear equation in three variables by mere substitution. In this method we find one of the three variables in terms of other two from any one of the equation and substitute it in the second equation. From the second equation we obtained the second variable in terms of the other and substitute it in the third equation and solve it to get the third variable which on re-substituting in the previous steps we get the other variables. It can also be solved by elimination method.


Solve the following system of linear equation: \[3x-y+4z=3,x+2y-3z=0\, and \,6x+5y=-3.\]
(a) \[x=-\frac{39}{10},y=\frac{47}{10},z=\frac{5}{2}\]
(b) \[x=\frac{39}{10},y=\frac{47}{10},z=\frac{5}{2}\]
(c) \[x=\frac{39}{10},y=\frac{7}{10},z=\frac{25}{2}\]
(d) \[x=-\frac{9}{10},y=\frac{17}{10},z=\frac{25}{2}\]
(e) None of these
Answer: (e)
Explanation
We have,
\[3x-y+4z=3-----\left( 1 \right)\]
\[x-2y-3z=-2-----\left( 2 \right)\]
\[6x+5y-5z=-3-----\left( 3 \right)\]
Form equation (1), we have
\[-y=3-3x-4x-----\left( 4 \right)\]
Putting in equation (2) the above value we get,
\[x=\frac{8-13z}{5}-----\left( 5 \right)\]
Putting equation (5) in (4) we get,
\[y=\frac{-9+13z}{5}-----\left( 6 \right)\]

Solve the following system of linear equation: \[5x-7y+z=11,6x-8y-z=15\,and\,3x+2y-6z=7.\]
(a) \[x=2,y=3,z=2\]
(b) \[x=-2,y=5,z=-1\]
(c) \[x=1,y=-1,z=-1\]
(d) \[x=-3,y=1,z=-2\]
(e) None of these
Answer: (c)

Solve the system of the equation: \[6x+y-3z=5,x+3y-2z=5,2x+y+4z=8\]
(a) \[x=1,y=2,z=1\]
(b) \[x=-2,y=5,z=-1\]
(c) \[x=1,y=-1,z=-1\]
(d) \[x=-3,y=1,z=-2\]
(e) None of these
Answer: (a)

Solve the system of equation: \[2y-3z=0,x+3y=-4,3x+4y=3\]
(a) \[x=2,y=3,z=2\]
(b) \[x=5,y=-3,z=-2\]
(c) \[x=4,y=-3,z=-1\]
(d) \[x=-2,y=2,z=-2\]
(e) None of these
Answer: (b)

Find the solution of the system of the equation: \[x+y=8,y+z=10,x+z=12\]
(a) \[x=5,y=3,z=2\]
(b) \[x=5,y=5,z=-1\]
(c) \[x=8,y=-2,z=-1\]
(d) \[x=5,y=3,z=7\]
(e) None of these
Answer: (d)

- The 6th Euler number is 61.
- 65 is the smallest number that becomes square if its reverse is either added to or subtracted from it.
- The smallest square which is the sum of 4 consecutive squares is 100.
- 8 years, 7 months & 6 days of yelling creates enough sound energy to heat 1 cup of coffee.
- Prior to 1900, prize fights lasted up to 100 rounds. Butterflies taste with their feet!

- Two equations in same variable are called pair of linear equation.
- A pair of linear equation can be solved by different methods: Such as substitution method, elimination method, and cross multiplication method.
- It can also be solved by graphical method.
- If the pair of line intersects each other at one point, then it is said to have unique solution and the point of intersection is the solution of the pair of equation.
- If the pair of line more...


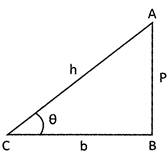 Then the trigonometrical ratios are defined as follows:
\[\sin \theta =\frac{\text{Perpendicual}}{\text{Hypotenuse}}=\frac{AB}{AC}\]
\[\cos \theta =\frac{Base}{\text{Hypotenuse}}=\frac{BC}{AC}\]
\[\tan \theta =\frac{\text{Perpendicular}}{Base}=\frac{AB}{BC}\]
\[\cot \theta =\frac{Base}{\text{Perpendicular}}=\frac{BC}{AB}\]
\[\sec \theta =\frac{\text{Hypotenuse}}{Base}=\frac{AC}{BC}\]
\[co\sec \theta =\frac{\text{Hypotenuse}}{\text{Perpendicular}}=\frac{AC}{AB}\] AB
If we represent perpendicular, base and hypotenuse by P, b and h respectively then the ratios can be written as:
Then the trigonometrical ratios are defined as follows:
\[\sin \theta =\frac{\text{Perpendicual}}{\text{Hypotenuse}}=\frac{AB}{AC}\]
\[\cos \theta =\frac{Base}{\text{Hypotenuse}}=\frac{BC}{AC}\]
\[\tan \theta =\frac{\text{Perpendicular}}{Base}=\frac{AB}{BC}\]
\[\cot \theta =\frac{Base}{\text{Perpendicular}}=\frac{BC}{AB}\]
\[\sec \theta =\frac{\text{Hypotenuse}}{Base}=\frac{AC}{BC}\]
\[co\sec \theta =\frac{\text{Hypotenuse}}{\text{Perpendicular}}=\frac{AC}{AB}\] AB
If we represent perpendicular, base and hypotenuse by P, b and h respectively then the ratios can be written as:
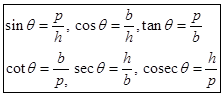 Relationship between Ratios
Relationship between Ratios
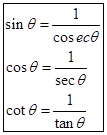 From the above, we conclude that sine of an angle is reciprocal to the cosec of that angle and so - on.
From the above, we conclude that sine of an angle is reciprocal to the cosec of that angle and so - on. 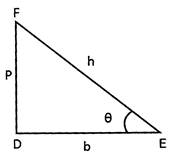 In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are
1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]
We can also derive different relations between identities in different form
(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]
or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]
Similarly
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]
(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]
Similarly
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
or \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]
(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
or \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]
or \[\cos e{{c}^{2}}\theta =\pm \sqrt{1+{{\cot }^{2}}\theta }\]
Similarly
\[{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta -1\]
or \[\cot \theta =\pm \sqrt{\cos e{{c}^{2}}\theta -1}\]
Verification of \[\mathbf{si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{\theta +co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{\theta =1}\]
Suppose \[\Delta \text{RST}\] is a right angled triangle in which right angle at R and angle S in formed at\[\theta \].
In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are
1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]
We can also derive different relations between identities in different form
(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]
or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]
Similarly
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]
(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]
Similarly
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
or \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]
(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
or \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]
or \[\cos e{{c}^{2}}\theta =\pm \sqrt{1+{{\cot }^{2}}\theta }\]
Similarly
\[{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta -1\]
or \[\cot \theta =\pm \sqrt{\cos e{{c}^{2}}\theta -1}\]
Verification of \[\mathbf{si}{{\mathbf{n}}^{\mathbf{2}}}\mathbf{\theta +co}{{\mathbf{s}}^{\mathbf{2}}}\mathbf{\theta =1}\]
Suppose \[\Delta \text{RST}\] is a right angled triangle in which right angle at R and angle S in formed at\[\theta \].
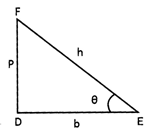 Here, perpendicular RT represented by "p", base RS represented by "b" and hypotenuse "ST" represented by h.
Then by Pythagoras theorem,
\[{{p}^{2}}+{{b}^{2}}={{h}^{2}}\]
As we know
\[\sin \theta =\frac{p}{h},\] \[\cos \theta =\frac{b}{h}\]
Therefore,
\[{{\sin }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}\,\,\text{and}\,\,{{\cos }^{2}}\theta =\frac{{{b}^{2}}}{{{h}^{2}}}\]
\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}+\frac{{{b}^{2}}}{{{h}^{2}}}=\frac{{{p}^{2}}+{{b}^{2}}}{{{h}^{2}}}=\frac{{{h}^{2}}}{{{h}^{2}}}=1\]
Therefore, \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
Similarly we can verify other results.
Here, perpendicular RT represented by "p", base RS represented by "b" and hypotenuse "ST" represented by h.
Then by Pythagoras theorem,
\[{{p}^{2}}+{{b}^{2}}={{h}^{2}}\]
As we know
\[\sin \theta =\frac{p}{h},\] \[\cos \theta =\frac{b}{h}\]
Therefore,
\[{{\sin }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}\,\,\text{and}\,\,{{\cos }^{2}}\theta =\frac{{{b}^{2}}}{{{h}^{2}}}\]
\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =\frac{{{p}^{2}}}{{{h}^{2}}}+\frac{{{b}^{2}}}{{{h}^{2}}}=\frac{{{p}^{2}}+{{b}^{2}}}{{{h}^{2}}}=\frac{{{h}^{2}}}{{{h}^{2}}}=1\]
Therefore, \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
Similarly we can verify other results.
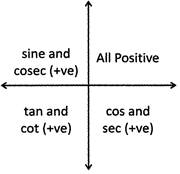
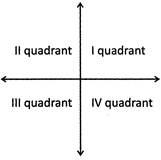 Above shows the different quadrants. The following are about the T- Ratios when angles lies in different quadrants
1. When the angle lies in the I quadrant all trigonometrical ratios are positive i.e. The value of \[\text{sin}\theta ,\text{ cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta ,\text{ sec}\theta \]and \[\text{cosec}\theta \] are positive.
2. When the angle\[''\theta ''\] lies in the second quadrant, the value of sine and cosec are positive and other ratios like \[\text{cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta \] and \[\text{sec}\theta \] are negative.
3. When an angle \[''\theta ''\] lies in third quadrant, the value of tan e and cote are positive and other ratios like \[\text{sin}\theta \text{,}\,\text{cos}\theta ,\text{ cosec}\theta \]and \[\sec \theta \] are negative.
4. When an angle \[''\theta ''\] lies in fourth quadrant, the value of \[\text{cos}\theta \text{ sec}\theta \] are positive and other ratios like \[\text{sin}\theta ,\text{ tan}\theta ,\text{ cosec}\theta \] and cote are negative.
From the figure given below you can remember it easily
Above shows the different quadrants. The following are about the T- Ratios when angles lies in different quadrants
1. When the angle lies in the I quadrant all trigonometrical ratios are positive i.e. The value of \[\text{sin}\theta ,\text{ cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta ,\text{ sec}\theta \]and \[\text{cosec}\theta \] are positive.
2. When the angle\[''\theta ''\] lies in the second quadrant, the value of sine and cosec are positive and other ratios like \[\text{cos}\theta ,\text{ tan}\theta ,\text{ cot}\theta \] and \[\text{sec}\theta \] are negative.
3. When an angle \[''\theta ''\] lies in third quadrant, the value of tan e and cote are positive and other ratios like \[\text{sin}\theta \text{,}\,\text{cos}\theta ,\text{ cosec}\theta \]and \[\sec \theta \] are negative.
4. When an angle \[''\theta ''\] lies in fourth quadrant, the value of \[\text{cos}\theta \text{ sec}\theta \] are positive and other ratios like \[\text{sin}\theta ,\text{ tan}\theta ,\text{ cosec}\theta \] and cote are negative.
From the figure given below you can remember it easily

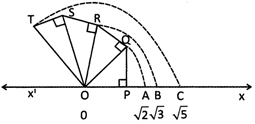
 The above given number line shows different rational numbers with denominator as 2.
Important Points Related to Number Line which Represents Rational Number
(i) A particular point on the number line represents a particular rational number.
(ii) A rational number cannot be represented by two or more than two distinct points on a number line.
(iii) There are infinite points between two distinct points on a line, hence, there are infinite rational numbers between two rational numbers.
Method to find Rational Numbers between Two Rational Numbers
(i) Suppose A and B be two rational number then a rational number which is in between A and B is \[\frac{1}{2}(A+B)\].
(ii) Suppose A and B be two rational number in which A < B, then the n rational numbers between A and B are \[(A+x),(A+2x),\] .............. \[(A+nx)\]. Where \[x=\frac{B-A}{n+1}\]
The above given number line shows different rational numbers with denominator as 2.
Important Points Related to Number Line which Represents Rational Number
(i) A particular point on the number line represents a particular rational number.
(ii) A rational number cannot be represented by two or more than two distinct points on a number line.
(iii) There are infinite points between two distinct points on a line, hence, there are infinite rational numbers between two rational numbers.
Method to find Rational Numbers between Two Rational Numbers
(i) Suppose A and B be two rational number then a rational number which is in between A and B is \[\frac{1}{2}(A+B)\].
(ii) Suppose A and B be two rational number in which A < B, then the n rational numbers between A and B are \[(A+x),(A+2x),\] .............. \[(A+nx)\]. Where \[x=\frac{B-A}{n+1}\]  Similarly diagrams given below shows
Similarly diagrams given below shows