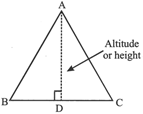
 Area of
\[\frac{4}{3}\pi \times {{6}^{3}}=\pi {{(0.2)}^{2}}\times h\]
Area of
\[\frac{4}{3}\pi \times {{6}^{3}}=\pi {{(0.2)}^{2}}\times h\]
 So, area of \[h=\frac{4\times {{6}^{3}}}{3\times {{(0.2)}^{2}}}=\frac{4\times 6\times 6\times 6}{3\times 0.04}\]
2. RECIANGLE
So, area of \[h=\frac{4\times {{6}^{3}}}{3\times {{(0.2)}^{2}}}=\frac{4\times 6\times 6\times 6}{3\times 0.04}\]
2. RECIANGLE
 ?
?
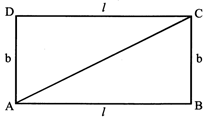
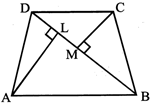 Area (A) of quadrilateral ABCD is given by:
A = (area of \[1{{m}^{2}}=10000c{{m}^{2}}\])+(area of \[1Kilolitre=1000litre\])
\[=1{{m}^{3}}\]
\[1acre=100acre\]
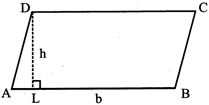
5. PARALLELOGRAM
Area (A) of quadrilateral ABCD is given by:
A = (area of \[1{{m}^{2}}=10000c{{m}^{2}}\])+(area of \[1Kilolitre=1000litre\])
\[=1{{m}^{3}}\]
\[1acre=100acre\]
5. PARALLELOGRAM
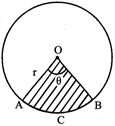 = Area of sector AOBC-Area of \[295c{{m}^{2}}\]
Length of \[\Delta ABC\] , where \[128c{{m}^{2}}\] more...
= Area of sector AOBC-Area of \[295c{{m}^{2}}\]
Length of \[\Delta ABC\] , where \[128c{{m}^{2}}\] more... 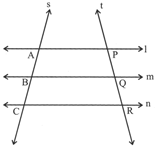 s and t are two transversal intersecting three parallel lines 1, m and n at A, B, C and P, Q, R, respectively
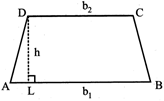
\[ABCD=\frac{1}{2}(AB+D\times CE)\] \[\angle R={{138}^{o}}\]
PARALLEL LINE AND TRANSVERSAL
If a transversal P intersect two parallel lines e|| m (as shown in the figure) then,
s and t are two transversal intersecting three parallel lines 1, m and n at A, B, C and P, Q, R, respectively
\[ABCD=\frac{1}{2}(AB+D\times CE)\] \[\angle R={{138}^{o}}\]
PARALLEL LINE AND TRANSVERSAL
If a transversal P intersect two parallel lines e|| m (as shown in the figure) then,
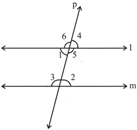 (i) Corresponding angles are equal
\[\angle R={{138}^{o}}\] {corresponding angles}
\[\angle ACB={{65}^{o}}\] {corresponding angles}
(ii) Alternate interior angles are equal
\[\angle ABC\] {alternate interior angles}
\[{{25}^{o}}\] {alternate interior angles}
(iii) Sum of consecutive interior angles in the same side of transversal is \[{{35}^{o}}\]
\[{{55}^{o}}\]
\[{{208}^{o}}\]
In the figure given below \[{{52}^{o}}\]
TRLANGLE
A triangle is a closed plane figure bound by three line segments. So, A triangle has six parts, three sides AB/BC and CA three angles \[\Delta XYZ\] and \[\Delta XYZ\]
(i) Corresponding angles are equal
\[\angle R={{138}^{o}}\] {corresponding angles}
\[\angle ACB={{65}^{o}}\] {corresponding angles}
(ii) Alternate interior angles are equal
\[\angle ABC\] {alternate interior angles}
\[{{25}^{o}}\] {alternate interior angles}
(iii) Sum of consecutive interior angles in the same side of transversal is \[{{35}^{o}}\]
\[{{55}^{o}}\]
\[{{208}^{o}}\]
In the figure given below \[{{52}^{o}}\]
TRLANGLE
A triangle is a closed plane figure bound by three line segments. So, A triangle has six parts, three sides AB/BC and CA three angles \[\Delta XYZ\] and \[\Delta XYZ\]
 Sum of all the angles in a triangle is \[{{60}^{o}}\]
\[{{30}^{o}}\] \[{{80}^{o}}\]
Median: The line segment joining a vertex of a triangle to the mid-point of the opposite side is called a median of the triangle.
(i) Intersecting point of the medians is called the centroid o the triangle.
(ii) Centroid divide the median in the ratio 2:1
Sum of all the angles in a triangle is \[{{60}^{o}}\]
\[{{30}^{o}}\] \[{{80}^{o}}\]
Median: The line segment joining a vertex of a triangle to the mid-point of the opposite side is called a median of the triangle.
(i) Intersecting point of the medians is called the centroid o the triangle.
(ii) Centroid divide the median in the ratio 2:1
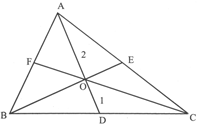 AD is the median \[{{100}^{o}}\]\[\angle DAC={{54}^{o}}\](median bisect opposite side)
AD, BE and CF are medians\[\angle ACB={{63}^{o}}\]O is centroid
So, \[{{(2.5)}^{2}}+{{(PT)}^{2}}={{(4.5)}^{2}}\] or \[\angle ACB={{63}^{o}}\]
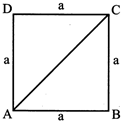
QUADRILATERAL
A closed figure with four sides is called quadrilateral
Quadrilateral ABCD has:
AD is the median \[{{100}^{o}}\]\[\angle DAC={{54}^{o}}\](median bisect opposite side)
AD, BE and CF are medians\[\angle ACB={{63}^{o}}\]O is centroid
So, \[{{(2.5)}^{2}}+{{(PT)}^{2}}={{(4.5)}^{2}}\] or \[\angle ACB={{63}^{o}}\]
QUADRILATERAL
A closed figure with four sides is called quadrilateral
Quadrilateral ABCD has:
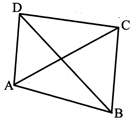 (i) Four sides: AB,BC, CD and DA.
(ii) Four vertices: A, B,C and D.
(iii) Four angles: \[{{(PT)}^{2}}=20.25-6.25=14\] and \[{{(PT)}^{2}}=PA\times PB\].
(iv) Two diagonals: AC and BD.
Properties of Quadrilateral
(i) Four sides: AB,BC, CD and DA.
(ii) Four vertices: A, B,C and D.
(iii) Four angles: \[{{(PT)}^{2}}=20.25-6.25=14\] and \[{{(PT)}^{2}}=PA\times PB\].
(iv) Two diagonals: AC and BD.
Properties of Quadrilateral
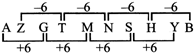 EXAMPLE 9:
Choose the missing term from the given options.
KM5, 1P8, GS11, EV14,
(a) BX17 (b) BY17
(c) CY18 (d) CY17
Sol. (d) Logic for the letters is -2, +3 steps, numbers added is 3.
EXAMPLE 9:
Choose the missing term from the given options.
KM5, 1P8, GS11, EV14,
(a) BX17 (b) BY17
(c) CY18 (d) CY17
Sol. (d) Logic for the letters is -2, +3 steps, numbers added is 3.
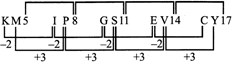 more...
more... 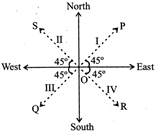 The candidate must distinguish between the regions and directions i.e. between North-East region and North-East direction.
If you move with your face east-wards, your left hand is towards north and your right hand is towards south. Similarly the positions of the directions of the hands can be fixed when you move in any of the other three directions.
To solve the question, first draw the direction figure
The candidate must distinguish between the regions and directions i.e. between North-East region and North-East direction.
If you move with your face east-wards, your left hand is towards north and your right hand is towards south. Similarly the positions of the directions of the hands can be fixed when you move in any of the other three directions.
To solve the question, first draw the direction figure
 on paper. Mark the starting point. After that move carefully according to the directions given in the question.
EXAMPLE 1:
Distance between e and g is:
(a) 2 km (b) 1 km
(c) 5 km (d) 1.5 km
EXAMPLE 2:
Distance between a and f is:
(a) 1.41 km (b) 3 km
(c) 2 km (d) 1 km
EXAMPLE 3:
Distance between e and i is:
(a) 4 km (b) 2 km
(c) 1 km (d) 3 km
Sol. (1-3):
From the information given, positions of houses are as follows:
on paper. Mark the starting point. After that move carefully according to the directions given in the question.
EXAMPLE 1:
Distance between e and g is:
(a) 2 km (b) 1 km
(c) 5 km (d) 1.5 km
EXAMPLE 2:
Distance between a and f is:
(a) 1.41 km (b) 3 km
(c) 2 km (d) 1 km
EXAMPLE 3:
Distance between e and i is:
(a) 4 km (b) 2 km
(c) 1 km (d) 3 km
Sol. (1-3):
From the information given, positions of houses are as follows:
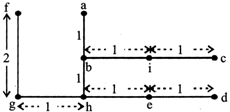 Sol. 1: (a)
Clearly, the distance between e and g is 2 km.
Sol. 2: (d)
From the above diagram, the distance between a and f is 1 km.
Sol.3: (c)
Clearly, the distance between e and i is 1km.
EXAMPLE 4:
In the given figure, P is 300 km eastward of O and Q is 400 kms North of O, R is exactly in the middle of Q and P. The distance between Q and R is :
(a) 250kms (b) \[250\sqrt{2}\] kms
(c) 300 kms (d) 350 kms
(e) None of these
Sol. (a) \[PQ=\sqrt{O{{P}^{2}}+O{{Q}^{2}}}\]
\[=\sqrt{{{(300)}^{2}}+{{(400)}^{2}}}=\sqrt{{{100}^{2}}({{3}^{2}}+{{4}^{2}})}\]
\[=\sqrt{{{100}^{2}}\times {{5}^{2}}}=(100\times 5)\] i.e., \[500km\]
R being in the midway of PQ, so QR= 250 kms.
EXAMPLE 5:
Four persons stationed at the four comers of a square piece as shown in the diagram. P starts crossing the field diagonally. After walking half the distance, he turns right, walks some distance and turns left.
Which direction is P facing now?
Sol. 1: (a)
Clearly, the distance between e and g is 2 km.
Sol. 2: (d)
From the above diagram, the distance between a and f is 1 km.
Sol.3: (c)
Clearly, the distance between e and i is 1km.
EXAMPLE 4:
In the given figure, P is 300 km eastward of O and Q is 400 kms North of O, R is exactly in the middle of Q and P. The distance between Q and R is :
(a) 250kms (b) \[250\sqrt{2}\] kms
(c) 300 kms (d) 350 kms
(e) None of these
Sol. (a) \[PQ=\sqrt{O{{P}^{2}}+O{{Q}^{2}}}\]
\[=\sqrt{{{(300)}^{2}}+{{(400)}^{2}}}=\sqrt{{{100}^{2}}({{3}^{2}}+{{4}^{2}})}\]
\[=\sqrt{{{100}^{2}}\times {{5}^{2}}}=(100\times 5)\] i.e., \[500km\]
R being in the midway of PQ, so QR= 250 kms.
EXAMPLE 5:
Four persons stationed at the four comers of a square piece as shown in the diagram. P starts crossing the field diagonally. After walking half the distance, he turns right, walks some distance and turns left.
Which direction is P facing now?
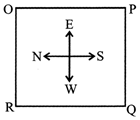 (a) North-east (b) North-west
(c) North (d) South-east
(e) South-west
Sol. (b)
The route of P is shown in the diagram.
Clearly the direction of P is North-west.
(a) North-east (b) North-west
(c) North (d) South-east
(e) South-west
Sol. (b)
The route of P is shown in the diagram.
Clearly the direction of P is North-west.
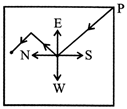 Miscellaneous Solved Examples
EXAMPLE 1:
Deepa moved more...
Miscellaneous Solved Examples
EXAMPLE 1:
Deepa moved more... 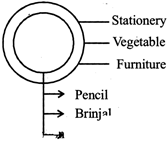 (i) Pencil, Stationery
(ii) Brinjal, Vegetable
(iii) Chair, Furniture
It is very clear from the above relationship that one object is a part of the other, and hence all such relationships can be represented by the figure shown.
Case II:
An object is said to have an intersection with in a other object that share some things in common.
(i) Surgeon, Males
(ii) Politicians, Indian
(iii) Educated, Unemployed
(i) Pencil, Stationery
(ii) Brinjal, Vegetable
(iii) Chair, Furniture
It is very clear from the above relationship that one object is a part of the other, and hence all such relationships can be represented by the figure shown.
Case II:
An object is said to have an intersection with in a other object that share some things in common.
(i) Surgeon, Males
(ii) Politicians, Indian
(iii) Educated, Unemployed
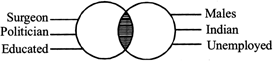 All the three relationships given above have something in common as some surgeons can be male and some female, some politicians may be Indian and some may belong to other countries, educated may be employed and unemployed as well and all the three relationships can be represented by the figure shown.
Case III:
Two objects are said to be disjoint when neither one is subset of another and nor do they share anything in common. In other words, totally unrelated objects fall under this type of relationship.
(i) Furniture, Car (ii) Copy, Cloth (iii) Tool, Shirt
All the three relationships given above have something in common as some surgeons can be male and some female, some politicians may be Indian and some may belong to other countries, educated may be employed and unemployed as well and all the three relationships can be represented by the figure shown.
Case III:
Two objects are said to be disjoint when neither one is subset of another and nor do they share anything in common. In other words, totally unrelated objects fall under this type of relationship.
(i) Furniture, Car (ii) Copy, Cloth (iii) Tool, Shirt
 It is clear from the above relationships that both the objects are unrelated to each other, and hence can be represented diagrammatically as shown in figure above. From the above discussion we observe that representation of the relationship between two objects is not typical if students follow the above points. But representation of three objects diagrammatically pose slight problems before the students.
ANALYTICAL METHOD:
Try to understand these type of questions using analytical method.
A statement always has a subject and a predicate:
All politicians are liars.
(subject) (predicate)
Basically, there are four types of sentences.
A - type \[\Rightarrow \] All politicians are liars.
I-type \[\Rightarrow \] Some politicians are liars
0-type \[\Rightarrow \] Some politicians are not liars
E-type \[\Rightarrow \] No politicians are liars
Conclusions can be drawn by taking two of the above statements together. The rules of conclusion are:
\[A+A=A\] \[A+E=E~\] \[I+A=I\]
\[I+E=0~~~~~~~\] \[E+A=0*~\] \[E+I=O*\]
Conclusion can only be drawn from the two statements if the predicate of the first statement is the subject of the second statement. The common term disappears in the conclusion and it consists of subject of the first statement and predicate of the second statement. For examples
\[A+A=A\]
(i) All boys are girls,
(ii) All girls are healthy
Conclusion: All boys are healthy.
\[A+E=E\] more...
It is clear from the above relationships that both the objects are unrelated to each other, and hence can be represented diagrammatically as shown in figure above. From the above discussion we observe that representation of the relationship between two objects is not typical if students follow the above points. But representation of three objects diagrammatically pose slight problems before the students.
ANALYTICAL METHOD:
Try to understand these type of questions using analytical method.
A statement always has a subject and a predicate:
All politicians are liars.
(subject) (predicate)
Basically, there are four types of sentences.
A - type \[\Rightarrow \] All politicians are liars.
I-type \[\Rightarrow \] Some politicians are liars
0-type \[\Rightarrow \] Some politicians are not liars
E-type \[\Rightarrow \] No politicians are liars
Conclusions can be drawn by taking two of the above statements together. The rules of conclusion are:
\[A+A=A\] \[A+E=E~\] \[I+A=I\]
\[I+E=0~~~~~~~\] \[E+A=0*~\] \[E+I=O*\]
Conclusion can only be drawn from the two statements if the predicate of the first statement is the subject of the second statement. The common term disappears in the conclusion and it consists of subject of the first statement and predicate of the second statement. For examples
\[A+A=A\]
(i) All boys are girls,
(ii) All girls are healthy
Conclusion: All boys are healthy.
\[A+E=E\] more... You need to login to perform this action.
You will be redirected in
3 sec
