 (2) When a pull is acting at an angle \[(\theta )\] to the horizontal (upward)
R + F sin \[\theta \] = mg
\[\Rightarrow \] R = mg - F sin \[\theta \]
and F cos \[\theta \] = ma
\[\therefore \] \[a=\frac{F\cos \theta }{m}\]
(2) When a pull is acting at an angle \[(\theta )\] to the horizontal (upward)
R + F sin \[\theta \] = mg
\[\Rightarrow \] R = mg - F sin \[\theta \]
and F cos \[\theta \] = ma
\[\therefore \] \[a=\frac{F\cos \theta }{m}\]
 (3) When a push is acting at an angle \[(\theta )\] to the horizontal (downward)
R = mg + F sin \[\theta \]
and F cos \[\theta \] = ma
\[a=\frac{F\cos \theta }{m}\]
(3) When a push is acting at an angle \[(\theta )\] to the horizontal (downward)
R = mg + F sin \[\theta \]
and F cos \[\theta \] = ma
\[a=\frac{F\cos \theta }{m}\]

| Condition | Free body diagram | Equation | Force and acceleration | ||||||||||||||
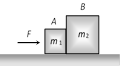 | | \[F-f={{m}_{1}}a\]. | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\] | ||||||||||||||
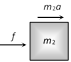 | \[f={{m}_{2}}a\] | \[f=\frac{{{m}_{2}}F}{{{m}_{1}}+{{m}_{2}}}\]. | |||||||||||||||
 |  | \[f={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}}\] | ||||||||||||||
| \[F-f={{m}_{2}}a\]. | \[f=\frac{{{m}_{1}}F}{{{m}_{1}}+{{m}_{2}}}\]. | ||||||||||||||||
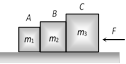
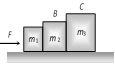 |   | \[F-{{f}_{1}}={{m}_{1}}a\] | \[a=\frac{F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] | ||||||||||||||
| | \[{{f}_{1}}=\frac{({{m}_{2}}+{{m}_{3}})F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. | ||||||||||||||||
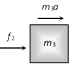
| \[{{f}_{2}}={{m}_{3}}a\]. | \[{{f}_{2}}=\frac{{{m}_{3}}F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]. | ||||||||||||||||
 | more...
Spring Balance and Physical Balance (1) Spring balance: When its upper end is fixed with rigid support and body of mass m hung from its lower end. Spring is stretched and the weight of the body can be measured by the reading of spring balance \[R=W=mg\]
 The mechanism of weighing machine is same as that of spring balance. Effect of frame of reference: In inertial frame of reference the reading of spring balance shows the actual weight of the body but in non-inertial frame of reference reading of spring balance increases or decreases in accordance with the direction of acceleration [for detail refer Article (4.13)] (2) Physical balance: In physical balance actually we compare the mass of body in both the pans. Here we does not calculate the absolute weight of the body. The mechanism of weighing machine is same as that of spring balance. Effect of frame of reference: In inertial frame of reference the reading of spring balance shows the actual weight of the body but in non-inertial frame of reference reading of spring balance increases or decreases in accordance with the direction of acceleration [for detail refer Article (4.13)] (2) Physical balance: In physical balance actually we compare the mass of body in both the pans. Here we does not calculate the absolute weight of the body. 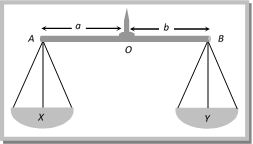 Here X and Y are the mass of the empty pan. (i) Perfect physical balance: Weight of the pan should be equal i.e. X = Y and the needle must in middle of the beam i.e. a = b. Effect of frame of reference: If the physical balance is perfect then there will be no effect of frame of reference (either inertial or non-inertial) on the measurement. It is always errorless. Here X and Y are the mass of the empty pan. (i) Perfect physical balance: Weight of the pan should be equal i.e. X = Y and the needle must in middle of the beam i.e. a = b. Effect of frame of reference: If the physical balance is perfect then there will be no effect of frame of reference (either inertial or non-inertial) on the measurement. It is always errorless. 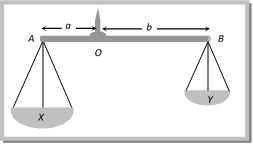 (ii) False balance: When the masses of the pan are not equal then balance shows the error in measurement. False balance may be of two types (a) If the beam of physical balance is horizontal (when the pans are empty) but the arms are not equal \[X>Y\] and \[a<b\] For rotational equilibrium about point ?O? \[Xa=Yb\] ?? (i) In this physical balance if a body of weight W is placed in pan X then to balance it we have to put a weight \[{{W}_{1}}\]in pan Y. For rotational equilibrium about point ?O? \[(X+W)\,a=(Y+{{W}_{1}})\,b\] ?.. (ii) Now if the pans are changed then to balance the body we have to put a weight \[{{W}_{2}}\] in pan X. For rotational equilibrium about point ?O? \[(X+{{W}_{2}})\,a=(Y+W)\,b\] ?? (iii) From (i), (ii) and (iii) True weight \[W=\sqrt{{{W}_{1}}\,{{W}_{2}}}\] (b) If the beam of physical balance is not horizontal (when the pans are empty) and the arms are equal i.e. \[X>Y\]and \[a=b\] In this physical balance if a body of weight W is placed in X Pan then to balance it. We have to put a weight \[{{W}_{1}}\] in Y Pan For equilibrium \[X+W=Y+{{W}_{1}}\] ?..(i) (ii) False balance: When the masses of the pan are not equal then balance shows the error in measurement. False balance may be of two types (a) If the beam of physical balance is horizontal (when the pans are empty) but the arms are not equal \[X>Y\] and \[a<b\] For rotational equilibrium about point ?O? \[Xa=Yb\] ?? (i) In this physical balance if a body of weight W is placed in pan X then to balance it we have to put a weight \[{{W}_{1}}\]in pan Y. For rotational equilibrium about point ?O? \[(X+W)\,a=(Y+{{W}_{1}})\,b\] ?.. (ii) Now if the pans are changed then to balance the body we have to put a weight \[{{W}_{2}}\] in pan X. For rotational equilibrium about point ?O? \[(X+{{W}_{2}})\,a=(Y+W)\,b\] ?? (iii) From (i), (ii) and (iii) True weight \[W=\sqrt{{{W}_{1}}\,{{W}_{2}}}\] (b) If the beam of physical balance is not horizontal (when the pans are empty) and the arms are equal i.e. \[X>Y\]and \[a=b\] In this physical balance if a body of weight W is placed in X Pan then to balance it. We have to put a weight \[{{W}_{1}}\] in Y Pan For equilibrium \[X+W=Y+{{W}_{1}}\] ?..(i) 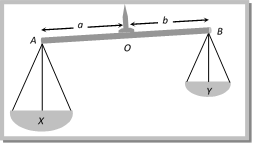 Now if pans are changed then to balance the body we have to put a weight \[{{W}_{2}}\] in X Pan. For equilibrium \[X+{{W}_{2}}=Y+W\] ?.. (ii) From (i) and (ii) True weight \[W=\frac{{{W}_{1}}+{{W}_{2}}}{2}\] Now if pans are changed then to balance the body we have to put a weight \[{{W}_{2}}\] in X Pan. For equilibrium \[X+{{W}_{2}}=Y+W\] ?.. (ii) From (i) and (ii) True weight \[W=\frac{{{W}_{1}}+{{W}_{2}}}{2}\]
Types of Friction (1) Static friction: The opposing force that comes into play when one body tends to move over the surface of another, but the actual motion has yet not started is called static friction. (i) If applied force is P and the body remains at rest then static friction F = P. (ii) If a body is at rest and no pulling force is acting on it, force of friction on it is zero. (iii) Static friction is a self-adjusting force because it changes itself in accordance with the applied force.
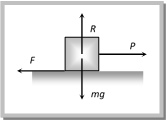 (2) Limiting friction: If the applied force is increased the force of static friction also increases. If the applied force exceeds a certain (maximum) value, the body starts moving. This maximum value of static friction upto which body does not move is called limiting friction. (i) The magnitude of limiting friction between any two bodies in contact is directly proportional to the normal reaction between them. \[{{F}_{l}}\propto R\] or \[{{F}_{l}}={{\mu }_{s}}R\] (ii) Direction of the force of limiting friction is always opposite to the direction in which one body is at the verge of moving over the other (iii) Coefficient of static friction: (a) \[{{\mu }_{s}}\] is called coefficient of static friction and defined as the ratio of force of limiting friction and normal reaction \[{{\mu }_{s}}=\frac{F}{R}\] (b) Dimension: \[[{{M}^{0}}{{L}^{0}}{{T}^{0}}]\] (c) Unit: It has no unit. (d) Value of \[{{\mu }_{s}}\] lies in between 0 and 1 (e) Value of \[\mu \] depends on material and nature of surfaces in contact that means whether dry or wet ; rough or smooth polished or non-polished. (f) Value of \[\mu \] does not depend upon apparent area of contact. (3) Kinetic or dynamic friction: If the applied force is increased further and sets the body in motion, the friction opposing the motion is called kinetic friction. (i) Kinetic friction depends upon the normal reaction. \[{{F}_{k}}\propto R\] or \[{{F}_{k}}={{\mu }_{k}}R\] where \[{{\mu }_{k}}\] is called the coefficient of kinetic friction (ii) Value of \[{{\mu }_{k}}\] depends upon the nature of surface in contact. (iii) Kinetic friction is always lesser than limiting friction \[{{F}_{k}}<{{F}_{l}}\] \[\therefore \,\,\,\,{{\mu }_{k}}<{{\mu }_{s}}\] i.e. coefficient of kinetic friction is always less than coefficient of static friction. Thus we require more force to start a motion than to maintain it against friction. This is because once the motion starts actually; inertia of rest has been overcome. Also when motion has actually started, irregularities of one surface have little time to get locked again into the irregularities of the other surface. (iv) Types of kinetic friction (a) Sliding friction: The opposing force that comes into play when one body is actually sliding over the surface of the other body is called sliding friction. e.g. A flat block is moving over a horizontal table. (b) Rolling friction: When objects such as a wheel (disc or ring), sphere or a cylinder rolls over a surface, the force of friction comes into play is more... (2) Limiting friction: If the applied force is increased the force of static friction also increases. If the applied force exceeds a certain (maximum) value, the body starts moving. This maximum value of static friction upto which body does not move is called limiting friction. (i) The magnitude of limiting friction between any two bodies in contact is directly proportional to the normal reaction between them. \[{{F}_{l}}\propto R\] or \[{{F}_{l}}={{\mu }_{s}}R\] (ii) Direction of the force of limiting friction is always opposite to the direction in which one body is at the verge of moving over the other (iii) Coefficient of static friction: (a) \[{{\mu }_{s}}\] is called coefficient of static friction and defined as the ratio of force of limiting friction and normal reaction \[{{\mu }_{s}}=\frac{F}{R}\] (b) Dimension: \[[{{M}^{0}}{{L}^{0}}{{T}^{0}}]\] (c) Unit: It has no unit. (d) Value of \[{{\mu }_{s}}\] lies in between 0 and 1 (e) Value of \[\mu \] depends on material and nature of surfaces in contact that means whether dry or wet ; rough or smooth polished or non-polished. (f) Value of \[\mu \] does not depend upon apparent area of contact. (3) Kinetic or dynamic friction: If the applied force is increased further and sets the body in motion, the friction opposing the motion is called kinetic friction. (i) Kinetic friction depends upon the normal reaction. \[{{F}_{k}}\propto R\] or \[{{F}_{k}}={{\mu }_{k}}R\] where \[{{\mu }_{k}}\] is called the coefficient of kinetic friction (ii) Value of \[{{\mu }_{k}}\] depends upon the nature of surface in contact. (iii) Kinetic friction is always lesser than limiting friction \[{{F}_{k}}<{{F}_{l}}\] \[\therefore \,\,\,\,{{\mu }_{k}}<{{\mu }_{s}}\] i.e. coefficient of kinetic friction is always less than coefficient of static friction. Thus we require more force to start a motion than to maintain it against friction. This is because once the motion starts actually; inertia of rest has been overcome. Also when motion has actually started, irregularities of one surface have little time to get locked again into the irregularities of the other surface. (iv) Types of kinetic friction (a) Sliding friction: The opposing force that comes into play when one body is actually sliding over the surface of the other body is called sliding friction. e.g. A flat block is moving over a horizontal table. (b) Rolling friction: When objects such as a wheel (disc or ring), sphere or a cylinder rolls over a surface, the force of friction comes into play is more...
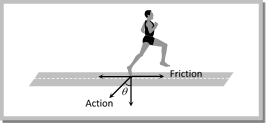
Friction is a Cause of Motion It is a general misconception that friction always opposes the motion. No doubt friction opposes the motion of a moving body but in many cases it is also the cause of motion. For example: (1) In moving, a person or vehicle pushes the ground backwards (action) and the rough surface of ground reacts and exerts a forward force due to friction which causes the motion. If there had been no friction there will be slipping and no motion.
 (2) In cycling, the rear wheel moves by the force communicated to it by pedalling while front wheel moves by itself. So, when pedalling a bicycle, the force exerted by rear wheel on ground makes force of friction act on it in the forward direction (like walking). Front wheel moving by itself experience force of friction in backward direction (like rolling of a ball). [However, if pedalling is stopped both wheels move by themselves and so experience force of friction in backward direction.] (2) In cycling, the rear wheel moves by the force communicated to it by pedalling while front wheel moves by itself. So, when pedalling a bicycle, the force exerted by rear wheel on ground makes force of friction act on it in the forward direction (like walking). Front wheel moving by itself experience force of friction in backward direction (like rolling of a ball). [However, if pedalling is stopped both wheels move by themselves and so experience force of friction in backward direction.] 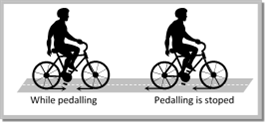 (3) If a body is placed in a vehicle which is accelerating, the force of friction is the cause of motion of the body along with the vehicle (i.e., the body will remain at rest in the accelerating vehicle until \[ma<{{\mu }_{s}}mg).\] If there had been no friction between body and vehicle the body will not move along with the vehicle. (3) If a body is placed in a vehicle which is accelerating, the force of friction is the cause of motion of the body along with the vehicle (i.e., the body will remain at rest in the accelerating vehicle until \[ma<{{\mu }_{s}}mg).\] If there had been no friction between body and vehicle the body will not move along with the vehicle. 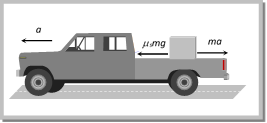 From these examples it is clear that without friction motion cannot be started, stopped or transferred from one body to the other. Sample problems based on fundamentals of friction Problem 1. If a ladder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor [AIIMS 2002] (a) 75 N (b) 50 N (c) 35 N (d) 25 N Solution: (a) Maximum force of friction \[{{F}_{l}}={{\mu }_{s}}R=0.3\times 250=75\,N\] Problem 2. On the horizontal surface of a truck \[(\mu = 0.6)\], a block of mass 1 kg is placed. If the truck is accelerating at the rate of \[5m/se{{c}^{2}}\] then frictional force on the block will be [CBSE PMT 2001] (a) 5 N (b) 6 N (c) 5.88 N (d) 8 N Solution: (a) Limiting friction \[={{\mu }_{s}}R={{\mu }_{s}}mg=0.6\times 1\times 9.8=5.88\,N\] When truck accelerates in forward direction at the rate of \[5m/{{s}^{2}}\] a pseudo force \[(ma)\] of 5N works on block in back ward direction. Here the magnitude of pseudo force is less than limiting friction So, static friction works in between the block and the surface of the truck and as we know, static friction = Applied force = 5 N. Problem 3. A block of mass 2 kg is kept on the floor. The coefficient of static friction is 0.4. If a force F of 2.5 N is applied on more... From these examples it is clear that without friction motion cannot be started, stopped or transferred from one body to the other. Sample problems based on fundamentals of friction Problem 1. If a ladder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor [AIIMS 2002] (a) 75 N (b) 50 N (c) 35 N (d) 25 N Solution: (a) Maximum force of friction \[{{F}_{l}}={{\mu }_{s}}R=0.3\times 250=75\,N\] Problem 2. On the horizontal surface of a truck \[(\mu = 0.6)\], a block of mass 1 kg is placed. If the truck is accelerating at the rate of \[5m/se{{c}^{2}}\] then frictional force on the block will be [CBSE PMT 2001] (a) 5 N (b) 6 N (c) 5.88 N (d) 8 N Solution: (a) Limiting friction \[={{\mu }_{s}}R={{\mu }_{s}}mg=0.6\times 1\times 9.8=5.88\,N\] When truck accelerates in forward direction at the rate of \[5m/{{s}^{2}}\] a pseudo force \[(ma)\] of 5N works on block in back ward direction. Here the magnitude of pseudo force is less than limiting friction So, static friction works in between the block and the surface of the truck and as we know, static friction = Applied force = 5 N. Problem 3. A block of mass 2 kg is kept on the floor. The coefficient of static friction is 0.4. If a force F of 2.5 N is applied on more...
Angle of Repose Angle of repose is defined as the angle of the inclined plane with horizontal such that a body placed on it is just begins to slide. By definition a is called the angle of repose. In limiting condition \[F=mg\,\sin \alpha \]
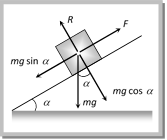 and \[R=mg\,\cos \alpha \] So \[\frac{F}{R}=\tan \alpha \] \[\therefore \,\,\,\,\frac{F}{R}=\mu =\tan \theta =\tan \alpha \] [As we know \[\frac{F}{R}=\mu =\tan \theta \]] Thus the coefficient of limiting friction is equal to the tangent of angle of repose. As well as \[\alpha =\theta \] i.e. angle of repose = angle of friction. Sample problems based on angle of friction and angle of repose Problem 7. A body of 5 kg weight kept on a rough inclined plane of angle \[{{30}^{o}}\] starts sliding with a constant velocity. Then the coefficient of friction is (assume \[\operatorname{g} = 10 m/{{s}^{2}}\]) [JIPMER 2002] (a) \[1/\sqrt{3}\] (b) \[2/\sqrt{3}\] (c) \[\sqrt{3}\] (d) \[2\sqrt{3}\] Solution: (a) Here the given angle is called the angle of repose So, \[\mu =\tan {{30}^{o}}=\frac{1}{\sqrt{3}}\] Problem 8. The upper half of an inclined plane of inclination q is perfectly smooth while the lower half is rough. A body starting from the rest at top comes back to rest at the bottom if the coefficient of friction for the lower half is given [Pb PMT 2000] (a) \[\operatorname{m}= sin\,\theta \] (b) \[\operatorname{m}= cot\,\theta \] (c) \[\operatorname{m}= 2 cos\,\theta \] (d) \[\operatorname{m}= 2 tan\,\theta \] and \[R=mg\,\cos \alpha \] So \[\frac{F}{R}=\tan \alpha \] \[\therefore \,\,\,\,\frac{F}{R}=\mu =\tan \theta =\tan \alpha \] [As we know \[\frac{F}{R}=\mu =\tan \theta \]] Thus the coefficient of limiting friction is equal to the tangent of angle of repose. As well as \[\alpha =\theta \] i.e. angle of repose = angle of friction. Sample problems based on angle of friction and angle of repose Problem 7. A body of 5 kg weight kept on a rough inclined plane of angle \[{{30}^{o}}\] starts sliding with a constant velocity. Then the coefficient of friction is (assume \[\operatorname{g} = 10 m/{{s}^{2}}\]) [JIPMER 2002] (a) \[1/\sqrt{3}\] (b) \[2/\sqrt{3}\] (c) \[\sqrt{3}\] (d) \[2\sqrt{3}\] Solution: (a) Here the given angle is called the angle of repose So, \[\mu =\tan {{30}^{o}}=\frac{1}{\sqrt{3}}\] Problem 8. The upper half of an inclined plane of inclination q is perfectly smooth while the lower half is rough. A body starting from the rest at top comes back to rest at the bottom if the coefficient of friction for the lower half is given [Pb PMT 2000] (a) \[\operatorname{m}= sin\,\theta \] (b) \[\operatorname{m}= cot\,\theta \] (c) \[\operatorname{m}= 2 cos\,\theta \] (d) \[\operatorname{m}= 2 tan\,\theta \]  Solution: (d) For upper half by the equation of motion \[{{v}^{2}}={{u}^{2}}+2as\] \[{{v}^{2}}={{0}^{2}}+2(g\sin \theta )l/2\]\[=gl\,\sin \theta \] [As \[u=0,\,s=l/2,\,a=g\,\sin \theta ]\] Solution: (d) For upper half by the equation of motion \[{{v}^{2}}={{u}^{2}}+2as\] \[{{v}^{2}}={{0}^{2}}+2(g\sin \theta )l/2\]\[=gl\,\sin \theta \] [As \[u=0,\,s=l/2,\,a=g\,\sin \theta ]\]  For lower half \[0={{u}^{2}}+2g(\sin \theta -\mu \cos \theta )\] 1/2 [As \[v=0,\,s=l/2,a=g\,(\sin \theta -\mu \cos \theta )\]] \[\Rightarrow \,\,\,0=gl\sin \theta +gl(\sin \theta -\mu \cos \theta )\] [As final velocity of upper half will be equal to the initial velocity of lower half] \[\Rightarrow \,\,2\sin \theta =\mu \cos \theta \Rightarrow \mu =2\tan \theta \] For lower half \[0={{u}^{2}}+2g(\sin \theta -\mu \cos \theta )\] 1/2 [As \[v=0,\,s=l/2,a=g\,(\sin \theta -\mu \cos \theta )\]] \[\Rightarrow \,\,\,0=gl\sin \theta +gl(\sin \theta -\mu \cos \theta )\] [As final velocity of upper half will be equal to the initial velocity of lower half] \[\Rightarrow \,\,2\sin \theta =\mu \cos \theta \Rightarrow \mu =2\tan \theta \]
Calculation of Necessary Force If W = weight of the body, \[\theta = angle of friction\], \[\mu =\tan \theta =\] coefficient of friction then we can calculate necessary force for different condition in the following manner:
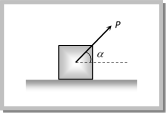 (1) Minimum pulling force P at an angle a from the horizontal By resolving P in horizontal and vertical direction (as shown in figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W-P\sin \alpha \] By substituting these value in \[F=\mu R\] (1) Minimum pulling force P at an angle a from the horizontal By resolving P in horizontal and vertical direction (as shown in figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W-P\sin \alpha \] By substituting these value in \[F=\mu R\] 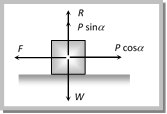 \[P\cos \alpha =\mu \,(W-P\sin \alpha )\] \[\Rightarrow \,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,\,(W-P\sin \alpha )\] [As \[\mu =\tan \theta \]] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha -\theta )}\] (2) Minimum pushing force P at an angle a from the horizontal \[P\cos \alpha =\mu \,(W-P\sin \alpha )\] \[\Rightarrow \,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,\,(W-P\sin \alpha )\] [As \[\mu =\tan \theta \]] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha -\theta )}\] (2) Minimum pushing force P at an angle a from the horizontal 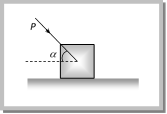 By Resolving P in horizontal and vertical direction (as shown in the figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W+P\sin \alpha \] By substituting these value in \[F=\mu R\] By Resolving P in horizontal and vertical direction (as shown in the figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W+P\sin \alpha \] By substituting these value in \[F=\mu R\] 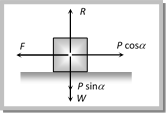 \[\Rightarrow \,\,\,\,\,\,\,\,\,P\cos \alpha =\mu \,(W+P\sin \alpha )\] \[\Rightarrow \,\,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,(W+P\sin \alpha )\,\,\,\,[As\,\,\mu =\tan \theta ]\] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha +\theta )}\] (3) Minimum pulling force P to move the body up an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium \[\Rightarrow \,\,\,\,\,\,\,\,\,P\cos \alpha =\mu \,(W+P\sin \alpha )\] \[\Rightarrow \,\,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,(W+P\sin \alpha )\,\,\,\,[As\,\,\mu =\tan \theta ]\] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha +\theta )}\] (3) Minimum pulling force P to move the body up an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium 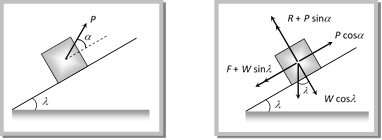 \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\,\sin \alpha \] and \[F+W\sin \lambda =P\cos \alpha \] \[\therefore \,\,\,\,\,\,\,\,\,F=P\cos \alpha -W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin \,(\theta +\lambda )}{\cos \,(\alpha -\theta )}\] (4) Minimum force on body in downward direction along the surface of inclined plane to start its motion By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\,\sin \alpha \] and \[F+W\sin \lambda =P\cos \alpha \] \[\therefore \,\,\,\,\,\,\,\,\,F=P\cos \alpha -W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin \,(\theta +\lambda )}{\cos \,(\alpha -\theta )}\] (4) Minimum force on body in downward direction along the surface of inclined plane to start its motion By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium 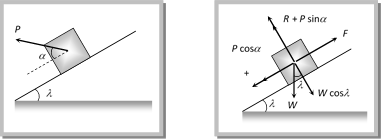 \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[F=P\cos \alpha +W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin (\theta -\lambda )}{\cos \,(\alpha -\theta )}\] (5) Minimum force to avoid sliding a body down an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[F=P\cos \alpha +W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin (\theta -\lambda )}{\cos \,(\alpha -\theta )}\] (5) Minimum force to avoid sliding a body down an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) 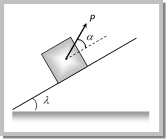 For the condition of equilibrium For the condition of equilibrium 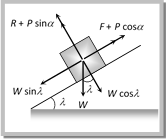 \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[P\cos \alpha +F=W\sin \lambda \] \ \[F=W\sin \lambda -P\cos \alpha \] By substituting these values in \[F=\mu R\] and solving we get \[P=W\,\left[ \frac{\sin \,(\lambda -\theta )}{\cos \,(\theta +\alpha )} \right]\] (6) Minimum force for motion and its direction \[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[P\cos \alpha +F=W\sin \lambda \] \ \[F=W\sin \lambda -P\cos \alpha \] By substituting these values in \[F=\mu R\] and solving we get \[P=W\,\left[ \frac{\sin \,(\lambda -\theta )}{\cos \,(\theta +\alpha )} \right]\] (6) Minimum force for motion and its direction 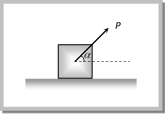 Let the force P be applied at an angle\[\alpha \]with the horizontal. By resolving P in horizontal more... Let the force P be applied at an angle\[\alpha \]with the horizontal. By resolving P in horizontal more...
When a body of mass m is placed on a weighing machine which is placed in a lift, then actual weight of the body is mg.
 This acts on a weighing machine which offers a reaction R given by the reading of weighing machine. This reaction exerted by the surface of contact on the body is the apparent weight of the body.
Apparent weight in a lift
This acts on a weighing machine which offers a reaction R given by the reading of weighing machine. This reaction exerted by the surface of contact on the body is the apparent weight of the body.
Apparent weight in a lift
|