\[\Rightarrow \] \[F\times S=\frac{{{P}^{2}}}{2m}\] [Where P = momentum of block]
\[\Rightarrow \] \[\mu mg\times S=\frac{{{P}^{2}}}{2m}\] [As F = m mg]
\[\Rightarrow \] \[S=\frac{{{P}^{2}}}{2\mu {{m}^{2}}g}\]
In the given condition P and \[\mu \] are same for both the blocks.
So, \[S\propto \frac{1}{{{m}^{2}}}\]; \[\therefore \] \[\frac{{{S}_{1}}}{{{S}_{2}}}={{\left[ \frac{{{m}_{2}}}{{{m}_{1}}} \right]}^{2}}\] 
\[ma=P-{{F}_{k}}\] \[\therefore \,\,\,\,\,\,\,a=\frac{P-{{F}_{k}}}{m}\] (2) Acceleration of a block down a rough inclined plane When angle of inclined plane is more than angle of repose, the body placed on the inclined plane slides down with an acceleration a.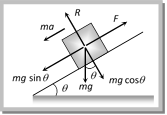 
From the figure \[ma=mg\sin \theta -F\] Þ \[ma=mg\sin \theta -\mu R\] Þ \[ma=mg\sin \theta -\mu \,mg\,\,\cos \theta \] \[\therefore \] Acceleration \[\therefore \,\,\,\,\,\,\,\,a=g\,[\sin \theta -\mu \cos \theta ]\] Note: q For frictionless inclined plane \[\mu =0\] \[\therefore a=g\sin \theta \]. (3) Retardation of a block up a rough inclined plane When angle of inclined plane is less than angle of repose, then for the upward motion 
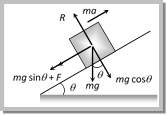\[ma=mg\,\,\sin \theta +F\] \[ma=mg\,\,\sin \theta +\mu \,mg\,\,\cos \theta \] Retardation \[a=g\,[\sin \theta +\mu \,\cos \theta ]\] Note: q For frictionless inclined plane \[\mu =0\] \[\therefore a=g\,\sin \theta \] Sample problems based on acceleration against friction Problem 11. A body of mass 10 kg is lying on a rough plane inclined at an angle of 30o to the horizontal and the coefficient of friction is 0.5. The minimum force required to pull the body up the plane is [JIPMER 2000] (a) 914 N (b) 91.4 N (c) 9.14 N (d) 0.914 N Solution: (b) \[F=mg(\sin \theta +\mu \cos \theta )\]\[=10\times 9.8\,(\sin 30+0.5\,\cos 30)=91.4\,N\] Problem 12. A block of mass 10 kg is placed on a rough horizontal surface having coefficient of friction \[\mu = 0.5\]. If a horizontal force of 100 N is acting on it, then acceleration of the block will be [AIIMS 2002] (a) \[0.5 m/{{s}^{2}}\] (b) \[5 m/{{s}^{2}}\] (c) \[10 m/{{s}^{2}}\] (d) \[15 m/{{s}^{2}}\] Solution: (b) \[a=\frac{\text{Applied }\,\text{force -- kinetic}\,\text{friction}}{\text{mass}}\]\[=\frac{100-0.5\times 10\times 10}{10}\]\[= 5m/{{s}^{2}}.\] Problem 13. A body of weight 64 N is pushed with just enough force to start it moving across a horizontal floor and the same force continues to act afterwards. If the coefficients of static and dynamic friction are 0.6 and 0.4 respectively, the acceleration of the body will be (Acceleration due to gravity = g) [EAMCET 2001] (a) \[\frac{g}{6.4}\] (b) 0.64 g (c) \[\frac{g}{32}\] (d) 0.2 g Solution: (d) Limiting friction \[={{F}_{1}}={{\mu }_{s}}R\Rightarrow \,\,64=0.6\text{ }m~g\Rightarrow m=\frac{64}{0.6\,g}\] \[Acceleration=\frac{\text{Applied force -- Kinetic}\,\,\text{ friction}}{\text{Mass of the body}}=\] \[\frac{64-{{\mu }_{K}}mg}{m}\]\[=\frac{64-0.4\times \frac{64}{0.6}}{\frac{64}{0.6g}}\,\,=\,\,0.2\,g\] Problem 14. If a block moving up at \[\theta ={{30}^{o}}\] with a velocity 5 m/s, stops after 0.5 sec, then what is \[\mu \] [CPMT 1995] (a) 0.5 (b) 1.25 (c) 0.6 (d) None of these Solution: (c) From \[v=u-at\Rightarrow 0=u-at\] \[\therefore \,\,\,\,t=\frac{u}{a}\] for upward motion on an inclined plane \[a=g(\sin \theta +\mu \cos \theta )\] \[\therefore \,\,\,\,\,\,\,\,t=\frac{u}{g(\sin \theta +\mu \cos \theta more... 
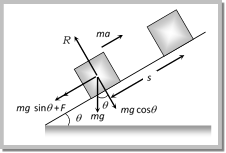\[\operatorname{Work} done = force\,\,\times \,\,distance\] \[= ma\,\,\times \,\,s\] \[= mg [sin\,\theta ~+m\,cos\,\theta ]\] \[=mg\,s\,[\sin \theta +\mu \cos \theta ]\] (2) Work done over a horizontal surface In the above expression if we put \[\theta = 0\] then \[\operatorname{Work} done = force\,\,\times \,\,distance\] \[= F\,\,\times \,\,s\] \[=\,\,\mu mg s\] 
It is clear that work done depends upon (i) Weight of the body. (ii) Material and nature of surface in contact. (iii) Distance moved. Sample problems based on work done against friction Problem 15. A body of mass 5kg rests on a rough horizontal surface of coefficient of friction 0.2. The body is pulled through a distance of 10m by a horizontal force of 25 N. The kinetic energy acquired by it is \[\left( g = 10 m{{s}^{2}} \right)\] [EAMCET (Med.) 2000] (a) 330 J (b) 150 J (c) 100 J (d) 50 J Solution: (b) Kinetic energy acquired by body = Total work done on the body ? Work done against friction \[\operatorname{F}\,\,\times \,\,S-\mu mg\,S\,= 25 \times 10 0.2 \times 5 \times 10 \times 10 = 250 100 = 150 J.= 25 \times 10 0.2 \times 5 \times 10 \times 10 = 250 100 = 150 J.\] Problem 16. 300 Joule of work is done in sliding a 2 kg. block up an inclined plane to a height of 10 meters. Taking value of acceleration due to gravity ?g? to be \[10 m/{{s}^{2}}\], work done against friction is [MP PMT 2002] (a) 100 J (b) 200 J (c) 300 J (d) Zero Solution: (a) Work done against gravity =\[~mgh = 2 \times 10 \times 10 = 200J\] Work done against friction = Total work done ? Work done against gravity \[= 300 200 = 100J.\] Problem 17. A block of mass 1 kg slides down on a rough inclined plane of inclination \[{{60}^{o}}\] starting from its top. If the coefficient of kinetic friction is 0.5 and length of the plane is 1 m, then work done against friction is \[\left( Take g = 9.8 m/{{s}^{2}} \right)\] [AFMC 2000; KCET (Engg./Med.) 2001] (a) 9.82 J (b) 4.94 J (c) 2.45J (d) 1.96 J Solution: (c) \[W=\mu mg\cos \theta .S=0.5\times 1\times 9.8\times \frac{1}{2}=2.45\text{ }J.\] Problem 18. A block of mass 50 kg slides over a horizontal distance of 1 m. If the coefficient of friction between their surfaces is 0.2, then work done against friction is [CBSE PMT 1999, 2000; AIIMS 2000; BHU 2001] (a) 98 J (b) 72J (c) 56 J (d) 34 J Solution: (a) \[W=\mu mgS=0.2\times 50\times 9.8\times 1=98J\]. 
(c) If L is the length of B as shown in figure A will fall from B after time t \[t=\sqrt{\frac{2L}{a}}=\sqrt{\frac{2mL}{F}}\] \[\left[ \text{As}\,\,\text{s}=\frac{\text{1}}{\text{2}}a\,{{t}^{2}}\,\text{and}\,\,a=F/m\, \right]\] (ii) If friction is present between A and B only and applied force is less than limiting friction (F < Fl) (F = Applied force on the upper body, \[{{\operatorname{F}}_{1}}=\] limiting friction between A and B, \[{{F}_{k}}=\] Kinetic friction between A and B) (a) The body A will not slide on body B till \[F<{{F}_{l}}\] i.e. \[F<{{\mu }_{s}}mg\] (b) Combined system (m + M) will move together with common acceleration \[{{a}_{A}}={{a}_{B}}=\frac{F}{M+m}\] (iii) If friction is present between A and B only and applied force is greater than limiting friction \[\left( F > {{F}_{1}} \right)\] In this condition the two bodies will move in the same direction (i.e. of applied force) but with different acceleration. Here force of kinetic friction \[{{\mu }_{k}}mg\] will oppose the motion of A while will cause the motion of B. \[F-{{F}_{k}}=m\,{{a}_{A}}\] i.e. \[{{a}_{A}}=\frac{F-{{F}_{k}}}{m}\] 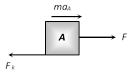 \[{{a}_{A}}=\frac{(F-{{\mu }_{k}}mg)}{m}\] | Free body diagram of A | \[{{F}_{k}}=M\,{{a}_{B}}\] i.e. \[{{a}_{B}}=\frac{{{F}_{k}}}{M}\] \ \[{{a}_{B}}=\frac{{{\mu }_{k}}mg}{M}\] 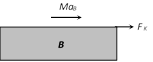 | Free body diagram of B |
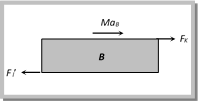However if B does not move then static friction will work (not limiting friction) between body B and the floor i.e. friction force = applied force \[\left( = {{F}_{k}} \right)\] not \[{{{F}'}_{l}}\]. (2) A force F is applied to the lower body, then following four more... 
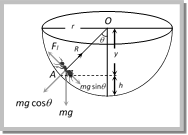Dividing (ii) by (i) \[\tan \theta =\frac{{{F}_{l}}}{R}=\mu \] \[\left[ \text{As}\,\,{{F}_{l}}=\mu R \right]\] \[\therefore \] \[\frac{\sqrt{{{r}^{2}}-{{y}^{2}}}}{y}=\mu \] or \[y=\frac{r}{\sqrt{1+{{\mu }^{2}}}}\] So \[h=r-y=r\,\left[ 1-\frac{1}{\sqrt{1+{{\mu }^{2}}}} \right]\], \[\therefore \,\,\,\,h=r\,\left[ 1-\frac{1}{\sqrt{1+{{\mu }^{2}}}} \right]\] Problem 22. An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle \[\alpha \] with the vertical, the maximum possible value of \[\alpha \] is given by [IIT-JEE (Screening) 2001] 
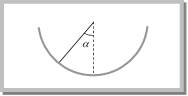(a) \[\cot \alpha =3\] (b) \[\tan \alpha =3\] (c) \[\sec \alpha =3\] (d) \[\text{cosec}\,\alpha =\text{3}\] Solution: (a) From the above expression, for the equilibrium \[R=mg\,\cos \,\alpha \,\text{and}\,F=mg\,\sin \,\alpha \]. Substituting these value in \[F=\mu R\] we get \[\tan \alpha =\mu \] or \[\cot \alpha =\frac{1}{\mu }=3\]. 
At limiting condition \[T={{F}_{l}}\] \[\Rightarrow \,\,\,\,\,{{m}_{2}}g=\mu R\] \[\Rightarrow \,\,\,\,\,{{m}_{2}}g=\mu \,{{m}_{1}}g\] \[\therefore \,\,\,\,{{m}_{2}}=\mu {{m}_{1}}\] this is the minimum value of \[{{m}_{2}}\] to start the motion. Note: q In the above condition Coefficient of friction \[\mu =\frac{{{m}_{2}}}{{{m}_{1}}}\] (2) When a mass m1 placed on a rough inclined plane: Another mass \[{{m}_{2}}\] hung from the string connected by pulley, the tension (T) produced in string will try to start the motion of mass \[{{m}_{1}}\].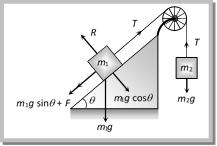 
At limiting condition For \[{{m}_{2}}\,\,\,\,\,\,\,T={{m}_{2}}g\] ...... (i) For \[{{m}_{1}}\,\,\,\,\,\,\,T={{m}_{1}}g\sin \theta +F\] Þ \[T={{m}_{1}}g\sin \theta +\mu R\] \[\Rightarrow \,\,\,\,\,T={{m}_{1}}g\sin \theta +\mu {{m}_{1}}g\cos \theta \] ...... (ii) From equation (i) and (ii) \[{{m}_{2}}={{m}_{1}}[\sin \theta +\mu \cos \theta ]\] this is the minimum value of \[{{m}_{2}}\] to start the motion Note: q In the above condition Coefficient of friction \[\mu =\left[ \frac{{{m}_{2}}}{{{m}_{1}}\cos \theta }-\tan \theta \right]\] Sample problems based on hung mass Problem 23. Two blocks of mass \[{{M}_{1}}\,\,and\,\,{{M}_{2}}\] are connected with a string passing over a pulley as shown in the figure. The block \[{{M}_{1}}\] lies on a horizontal surface. The coefficient of friction between the block \[{{M}_{1}}\] and horizontal surface is \[\mu \]. The system accelerates. What additional mass m should be placed on the block \[{{M}_{1}}\] so that the system does not accelerate. 
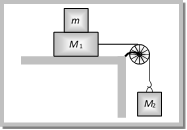(a) \[\frac{{{M}_{2}}-{{M}_{1}}}{\mu }\] (b) \[\frac{{{M}_{2}}}{\mu }-{{M}_{1}}\] (c) \[{{M}_{2}}-\frac{{{M}_{1}}}{\mu }\] (d) \[({{M}_{2}}-{{M}_{1}})\mu \] Solution: (b) By comparing the given condition with general expression \[\mu =\frac{{{M}_{2}}}{m+{{M}_{1}}}\Rightarrow m+{{M}_{1}}=\frac{{{M}_{2}}}{\mu }\Rightarrow m=\frac{{{M}_{2}}}{\mu }-{{M}_{1}}\] 
Problem 24. The coefficient of kinetic friction is 0.03 in the diagram where mass \[{{m}_{2}}=20\,kg\] and \[{{m}_{1}}=4\,kg\]. The acceleration of the block shall be \[(g=10m{{s}^{-2}})\] (a) \[1.8\,\,m{{s}^{-2}}\] (b) \[0.8\,\,m{{s}^{-2}}\] (c) \[1.4\,\,m{{s}^{-2}}\] (d) \[0.4\,\,m{{s}^{-2}}\] 
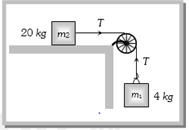Solution: (c) Let the acceleration of the system is a From the F.B.D. of \[{{m}_{2}}\] 
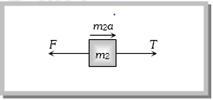\[T-F={{m}_{2}}a\Rightarrow T-\mu {{m}_{2}}g={{m}_{2}}a\] \[\Rightarrow T-0.03\times 20\times 10=20\,a\Rightarrow T-6=20a\] ..... (i) From the FBD of \[{{m}_{1}}\] \[{{m}_{1}}g-T={{m}_{1}}a\] 
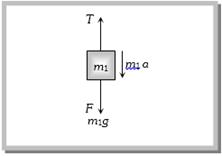\[\Rightarrow 4\times 10-T=4a\Rightarrow 40-T=4a\] .... (ii) Solving (i) and (ii) \[a=1.4m/{{s}^{2}}.\] 
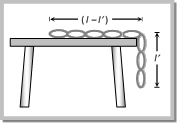\[\mu =\frac{\text{length hanging from the table}}{\text{length lying on the table}}\] [As chain have uniform linear density] \[\therefore \,\,\,\,\mu =\frac{{{l}'}}{l-{l}'}\] by solving \[{l}'=\frac{\mu \,l}{(\mu +1)}\] Problem 25. A heavy uniform chain lies on a horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum fraction of the length of the chain that can hang over one edge of the table is [CBSE PMT 1990] (a) 20% (b) 25% (c) 35% (d) 15% Solution: (a) From the expression \[l'=\left( \frac{\mu }{\mu +1} \right)\,l\] \[=\left( \frac{0.25}{0.25+1} \right)\,l\] [As \[\mu = 0.25\]] \[\Rightarrow \,\,\,l'=\frac{0.25}{1.25}l=\frac{l}{5}=20\,%\] of the length of the chain. 
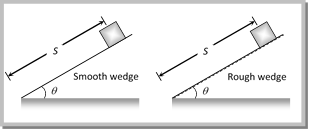If the same wedge made rough then time taken by it to come down becomes n times more (i.e. nt) The length of path in both the cases are same. | For smooth wedge \[S=u\,t+\frac{1}{2}a{{t}^{2}}\] \[S=\frac{1}{2}(g\,\sin \theta )\,{{t}^{2}}\] .....(i) \[[\text{As}\,u=0\,\text{and }\]\[a=g\sin \theta ]\] | For rough wedge \[S=u\,t+\frac{1}{2}a{{t}^{2}}\] \[S=\frac{1}{2}g\,(\sin \theta -\mu \cos \theta )\,{{(nt)}^{2}}\] .....(ii) \[[\text{As}\,u=0\,\text{and}\,a=g\,(\sin \theta -\mu \,\cos \theta )]\] |
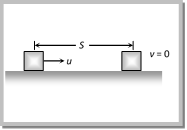\[\Rightarrow \,\,\,ma=\mu \,mg\] \[\therefore \,\,\,\,\,\,\,\,a=\mu g\] From \[{{\operatorname{v}}^{2}}={{u}^{2}}-2aS\Rightarrow \,\] \[0={{u}^{2}}-2\mu \,g\,S\,\] \[\text{ }\!\![\!\!\text{ As}\,\,v=0,\,\,a=\mu g]\] \[\therefore \,\,\,\,\,\,S=\frac{{{u}^{2}}}{2\mu g}\] or \[S=\frac{{{P}^{2}}}{2\mu {{m}^{2}}g}\] [As momentum P = mu] (ii) Time taken to come to rest From equation \[v=u-a\,t\Rightarrow \] \[0=u-\mu \,g\,t\] \[[\text{As}\,\,\,v=0,\,a=\mu \,g]\] \[\therefore \,\,\,t=\frac{u}{\mu g}\] (iii) Force of friction acting on the body We know, F = ma So, \[F=m\frac{(v-u)}{t}\] \[F=\frac{mu}{t}\] [As v = 0] \[F=\mu \,mg\] \[\left[ \text{As}\,\,t=\frac{u}{\mu g} \right]\] (2) On inclined road : When block starts with velocity u its kinetic energy will be converted into potential energy and some part of it goes against friction and after travelling distance S it comes to rest i.e. v = 0. And we know that retardation \[a=g\,[\sin \theta +\mu \cos \theta ]\] By substituting the value of v and a in the following equation 
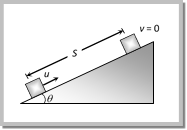\[{{v}^{2}}={{u}^{2}}-2a\,S\] \[\Rightarrow \,\,\,\,0={{u}^{2}}-2g\,[\sin \theta +\mu \cos \theta ]\,S\] \[\therefore \,\,\,\,\,S=\frac{{{u}^{2}}}{2g\,(\sin \theta +\mu \cos \theta )}\] Sample problems based on motion of body on rough surface Problem 27. A marble block of mass 2 kg lying on ice when given a velocity of 6 m/s is stopped by friction in 10s. Then the coefficient of friction is [AIEEE 2003] (a) 0.01 (b) 0.02 (c) 0.03 (d) 0.06 Solution: (d) \[v=u-at\] \[=u-\mu g\,t=0\] \[\therefore \,\,\,\,\,\,\mu =\frac{u}{gt}=\frac{6}{10\times 10}=0.06\] Problem 28. A 2 kg mass starts from rest on an inclined smooth surface with inclination \[{{30}^{o}}\] and length 2 m. How much will it travel before coming to rest on a surface with coefficient of friction 0.25 [UPSEAT 2003] (a) 4 m (b) 6 m (c) 8 m (d) 2 m Solution: (a) \[{{v}^{2}}={{u}^{2}}+2aS\]\[=0+2\times g\sin 30\times 2\] \[v=\sqrt{20}\] Let it travel distance ?S? before coming to rest \[S=\frac{{{v}^{2}}}{2\mu g}=\frac{20}{2\times 0.25\times 10}=4m.\] 
Friction force (F) = weight of person (mg) \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mu R = mg\] \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mu \,{{F}_{c}}=mg\] [Here, \[{{\operatorname{F}}_{c}}= centrifugal force\]] \[\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mu m\omega _{\min }^{2}r=mg\] \[\therefore \,\,\,\,\,\,\,\,\,{{\omega }_{\min }}=\sqrt{\frac{g}{\mu \,r}}\] Sample Problems (Miscellaneous) Problem 29. A motorcycle is travelling on a curved track of radius 500m if the coefficient of friction between road and tyres is 0.5. The speed avoiding skidding will be [MH CET (Med.) 2001] (a) 50 m/s (b) 75 m/s (c) 25 m/s (d) 35 m/s Solution: (a) \[v=\sqrt{\mu rg}=\sqrt{0.5\times 500\times 10}=50\,m/s.\] Problem 30. A horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is [AIEEE 2003]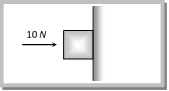 
(a) 2 N (b) 20 N (c) 50 N (d) 100 N Solution: (a) For equilibrium 
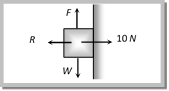Weight (W) = Force of friction (F) \[W=\mu R=0.2\times 10=2\,N\] Problem 31. A body of mass 2 kg is kept by pressing to a vertical wall by a force of 100 N. The friction between wall and body is 0.3. Then the frictional force is equal to [Orissa JEE 2003] (a) 6 N (b) 20 N (c) 600 N (d) 700 N Solution: (b) For the given condition Static friction = Applied force = Weight of body \[= 2 \times 10 = 20 N.\] Problem 32. A fireman of mass 60kg slides down a pole. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is 0.5, with what acceleration will the fireman slide down \[\left( g = 10 m/{{s}^{2}} \right)\] [Pb. PMT 2002] (a) \[1 m/{{s}^{2}}\] (b) \[2.5 m/{{s}^{2}}\] (c) \[10 m/{{s}^{2}}\] (d) \[5 m/{{s}^{2}}\] 
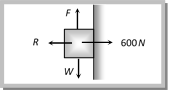Solution: (d) \[\operatorname{Friction} =mR = 0.5 \times 600 = 300 N, \,Weight = 600 N\] \[\therefore \,\,\,\,\,\,\,a=5\,m/{{s}^{2}}\] Problem 33. The system shown in the figure is in equilibrium. The maximum value of W, so that the maximum value of static frictional force on 100 kg body is 450 N, will be 
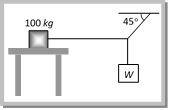(a) 100 N (b) 250 N (c) 450 N (d) 1000 N Solution: (c) For vertical equilibrium \[{{T}_{1}}\sin {{45}^{o}}=W\] 
You need to login to perform this action.
You will be redirected in
3 sec
