INTEGERS
FUNDAMENTALS
- In lower classes, you would have read about counting number. 1, 2, 3,.........
- They are called natural numbers (N).
N= (1, 2, 3, 4,............)
Elementary Question - 1: Which is the smallest natural number?
Ans.: 1
- Representation of natural numbers on a number line. To represent natural numbers on a number line, we should draw a line and write the number at equal distances on it as shown below:
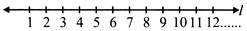
- Whole Number (W): The set of natural numbers together with zero is known as the set of whole numbers.
Elementary Question - 2: Which is the smallest whole number?
Ans.: 0
W= (0, 1, 2, 3,............)
- In set notation, set of whole numbers (W) = set of natural numbers (N) + zero; { } is used for set notation.
- Integers (Z): The set containing negatives of natural numbers along with whole numbers is called the set of integers.
That is, \[Z=\{........-4,\,\,-3,\,\,-2,\,\,-1\}\cup \{0,\text{ }1,\,\,2,\,\,3,\,\,4,\,\,5,.....\}\]
Where \[\cup \] denote "union" or combination of these two sets.
Concept of Infinity
We can go on adding more and more numbers to the right side of the number line (e.g., 100, 101, ......100000, .........1 crore, ............1000 crores............. m an unending manner upto plus infinity and similarly to the left side of the number line upto minus infinity.
\[\left( -\,\infty \right)\]Minus infinity crore
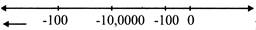
Plus infinity \[\left( +\infty \right)\]
This very, very large unending number on the right side and left side of number line are called plus infinity \[\left( +\,\infty \right)\]and minus infinity \[\left( -\,\infty \right)\] respectively.
\[\left( -\,\infty \right)\]
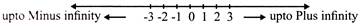
\[\left( +\,\infty \right)\]

Note:
Usually, negative numbers are placed in brackets to avoid confusion arising due to two signs in evaluations simultaneously,
e.g., \[3+\left( -\,5 \right)=-2\]
2.0 is not included in either \[{{Z}^{+}}\]c or\[{{Z}^{-}}\]. Hence, it is non-negative integer
Common use of numbers
(i) To represent quantities like profit, income, increase, rise, high, north, east, above, depositing, climbing and so on, positive numbers are used.
(ii) To represent quantities like loss, expenditure, decrease, fall, low, south, west, below, withdrawing, sliding and so on, negative numbers are used.
(iii) On a number line, when we
Add a positive integer, we move to the right.
Add a negative integer, we move to the left.
Subtract a positive integer, we move to the left.
Subtract a negative integer, we move to the right
Notation e means belongs to; a, b \[\in \] means the numbers a and b belong to \[\] (set of integers)
Note:
0 is neither positive nor negative.
The + sign is not written before a positive number
\[\frac{1}{2}\] and 0.3 are more...
 Note:
Note:
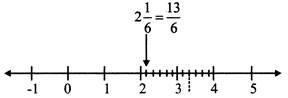
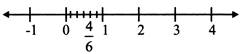 Representation of \[\frac{p}{q}\]on the number line where p > q:
Consider the rational number \[\frac{13}{6}\]
Let us convert the rational number \[\frac{13}{6}\] into a mixed fraction \[=2\frac{1}{6}\]and then mark it on the number line. i.e.
Representation of \[\frac{p}{q}\]on the number line where p > q:
Consider the rational number \[\frac{13}{6}\]
Let us convert the rational number \[\frac{13}{6}\] into a mixed fraction \[=2\frac{1}{6}\]and then mark it on the number line. i.e.
 FUNDAMENTALS
FUNDAMENTALS
 more...
more... 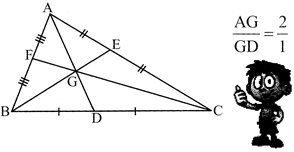 FUNDAMENTALS
FUNDAMENTALS
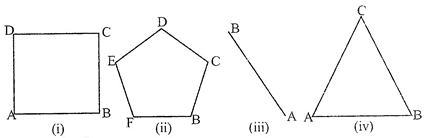 The figure (iv) is a triangle
The figure (iv) is a triangle
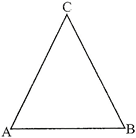 Its sides are AB, BC, CA and angles are \[\angle A,\angle B,\angle C\] (also written as \[\angle BAC,\angle CBA\]and \[\angle ACB\]). These are six elements and its vertices are points A, B, C.
Its sides are AB, BC, CA and angles are \[\angle A,\angle B,\angle C\] (also written as \[\angle BAC,\angle CBA\]and \[\angle ACB\]). These are six elements and its vertices are points A, B, C.
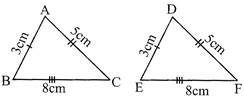 In the given figure, \[\Delta \,ABC=\cong \Delta \,DEF\] by S. S. S. congruence condition.
In the given figure, \[\Delta \,ABC=\cong \Delta \,DEF\] by S. S. S. congruence condition.
