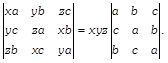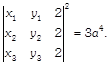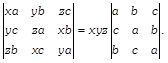-
If the vertices A,B,C of a \[\Delta ABC\] have position vectors (1, 2, 3), \[(-\,1,\,\,0,\,\,0)\] and (0, 1, 2) respectively, what is the magnitude of \[\angle ABC?\]
View Answer play_arrow
-
If \[A=\left[ \begin{matrix} 0 & a \\ 0 & 0 \\ \end{matrix} \right],\] find \[{{A}^{16}}.\]
View Answer play_arrow
-
Evaluate \[\int_{0}^{1}{\log \left( \frac{1-x}{x} \right)\,dx.}\]
View Answer play_arrow
-
If \[x=a\,\sin \,mt-b\,\cos \,mt\] and \[\frac{{{d}^{2}}x}{d{{t}^{2}}}=\mu x,\] then find the value of \[\mu .\]
View Answer play_arrow
-
If \[A({{x}_{1}},\,\,{{y}_{1}}),\] \[B({{x}_{2}},\,\,{{y}_{2}})\] and \[C({{x}_{3}},\,\,{{y}_{3}})\] are vertices of an equilateral triangle whose each side is equal to a, then prove that
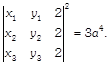
-
If \[y={{\tan }^{-1}}x,\] find \[\frac{{{d}^{2}}y}{d{{x}^{2}}}\] in terms of y alone.
View Answer play_arrow
-
Find \[\lambda ,\] when projection of \[\vec{a}=\lambda \hat{i}+\hat{j}+4\hat{k}\] on \[\vec{b}=2\hat{i}+6\hat{j}+3\hat{k}\] is 4 units.
View Answer play_arrow
-
At what point on the curve \[y={{x}^{2}}\] does the tangent make an angle of \[45{}^\circ \] with the X-axis?
View Answer play_arrow
-
\[f(x)=\left\{ \begin{matrix} \frac{|x-4|}{2(x-4)}, & \text{if}\,\,x\ne 4 \\ 0, & \text{if}\,\,x=4 \\ \end{matrix}at\,\,x=4. \right.\]
View Answer play_arrow
-
Find an angle \[\theta ,\,\,0<\theta <\frac{\pi }{2},\] which increases twice as fast as it sine.
View Answer play_arrow
-
Evaluate \[\int{{{\sin }^{4}}x}{{\cos }^{4}}x\,\,dx.\]
View Answer play_arrow
-
In a hurdles race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is \[\frac{5}{6}.\] What is the probability that he will knock down fewer than 2 hurdles?
View Answer play_arrow
-
Two farmers Ramkrishna and Gurcharan Singh cultivates only three crops rice, maize and wheat. The sales (in Rs.) of these crops in the month of July and August are given by the following matrices. July sales \[\begin{align} & \text{Rice}\,\,\,\,\,\,\,\,\text{Maize}\,\,\,\,\,\text{Wheat} \\ & A=\left[ \begin{matrix} 15000 & 10000 & 50000 \\ 45000 & 20000 & 25000 \\ \end{matrix} \right]\begin{matrix} \text{Ramkishan} \\ \text{Gurcharan}\,\,\text{singh} \\ \end{matrix} \\ \end{align}\] August sales \[\begin{align} & \text{Rice}\,\,\,\,\,\,\text{Maize}\,\,\,\,\,\,\,\,\,\text{Wheat} \\ & A=\left[ \begin{matrix} 10000 & 15000 & 20000 \\ 15000 & 5000 & 25000 \\ \end{matrix} \right]\begin{matrix} \text{Ramkishan} \\ \text{Gurcharan}\,\,\text{singh} \\ \end{matrix} \\ \end{align}\] (i) Find the combined sales in July and August for each farmer in each crop. (ii) If both farmers receive 1.5% profit on gross sales. Compute the profit for each farmer for crop sold in July. (iii) Give suggestions to the farmers keeping 'Save Environment' in mind.
View Answer play_arrow
-
Solve \[{{\sin }^{-1}}x+{{\sin }^{-1}}(1-x)={{\cos }^{-1}}x.\]
View Answer play_arrow
-
Form the differential equation having \[y={{({{\sin }^{-1}}x)}^{2}}+A{{\cos }^{-1}}x+B,\] where A and B are arbitrary constants, as its general solution.
View Answer play_arrow
-
If \[y=x\log \left( \frac{x}{a+bx} \right),\] then prove that \[{{x}^{3}}\frac{{{d}^{2}}y}{d{{x}^{2}}}={{\left( x\frac{dy}{dx}-y \right)}^{2}}.\]
View Answer play_arrow
-
Evaluate \[\int{{{e}^{x}}\left( \frac{\sin 4x-4}{1-\cos 4x} \right)}\,dx.\]
View Answer play_arrow
-
| Evaluate \[\int_{3}^{4}{\frac{\sqrt{x}}{\sqrt{x}+\sqrt{7-x}}dx.}\] |
| OR |
| Evaluate \[\int_{0}^{1}{\frac{\log (1+x)}{1+{{x}^{2}}}\,dx.}\] |
View Answer play_arrow
-
| A company has two plants for manufacturing scooters. Plant I manufactures 70% of the scooters and plant II manufactures 30% of the scooters. At plant I, 30% of the scooters are maintaining pollution norms and plant II, 90% of the scooters are maintaining pollution norms. A scooter chosen at random and is found to be fit oh pollution norms. Find the probability that it has come from plant II. |
| OR |
| Events A and B are such that \[P(A)=\frac{1}{2},\] \[P(B)=\frac{7}{12}\] and P (not A or not B) \[=\frac{1}{4}.\] State whether A and B are independent. |
View Answer play_arrow
-
If \[\vec{a},\,\,\vec{b}\] and \[\vec{c}\] are three vectors, such that \[|\vec{a}|\,\,=3,\] \[|\vec{b}|\,\,=4\] and \[|\vec{c}|\,\,=5\] and each one of these is perpendicular to the sum of other two, find \[|\vec{a}+\vec{b}+\vec{c}|.\]
View Answer play_arrow
-
| Find the coordinates of point on line \[\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{6},\] which are at a distance of 3 units from the point \[(1,\,\,-2,\,\,3).\] |
| OR |
| Show that the lines \[\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda (3\hat{i}-\hat{j})\] and \[\vec{r}-=(4\hat{i}-\hat{k})+\mu (2\hat{i}+3\hat{k})\] are coplanar. Also, find the equation of the plane containing them. |
View Answer play_arrow
-
Find the particular solution of the differential equation \[\frac{dy}{dx}+y\cot x=2x+{{x}^{2}}\cot x(x\ne 0),\] given that \[y=0\] when \[x=\frac{\pi }{2}.\]
View Answer play_arrow
-
A bag contains 25 balls of which 10 are purple and the remaining are pink. A ball is drawn at random, its colour is noted and it is replaced. 6 balls are drawn in this way. Find the probability that (i) All balls were purple, (ii) Not more than 2 were pink. (iii) An equal number of purple and pink balls were drawn. (iv) atleast one ball was pink.
View Answer play_arrow
-
| Consider \[f:{{R}^{+}}\to [-\,9,\,\,\infty ]\] given by \[f(x)=5{{x}^{2}}+6x-9.\] Prove that f is invertible with \[{{f}^{-1}}(y)=\left( \frac{\sqrt{54+5y}-3}{5} \right)\] |
| (Where, \[{{R}^{+}}\] is the set of all positive real numbers). |
| OR |
| Let '*' be a binary operation on the set |
| {0, 1, 2, 3, 4, 5} defined as |
| \[a*b=\left\{ \begin{matrix} a+b, & \text{if}\,\,a+b<6 \\ a+b-6, & \text{if}\,\,a+b\ge 6 \\ \end{matrix} \right.\] |
| Show that zero is the identity for this operation and each element a of the set is invertible with \[b-a,\] being the inverse of a. |
View Answer play_arrow
-
If a young man rides his motor-cycle at 25 km per hour, he had to spend Rs. 2 per km on petrol with very little pollution in the air. If he rides if at a faster speed of 40 km per hour, the petrol cost increases to Rs. 5 per km and rate of pollution also increases. He has Rs. 100 to spend on petrol and wishes to find what is the maximum distance he can travel within one hour. Express this problem as an LPP Solve it graphically to find the distance to be covered with different speeds. What value is indicated in this question?
View Answer play_arrow
-
| Find the equation of the plane passing through the line of intersection of planes |
| \[2x+y-z=3,\] \[5x-3y+4z+9=0\] and parallel to the line \[\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-5}{5}.\] |
| OR |
| Find the distance of the point \[(-\,2,\,\,3,\,\,-4)\] from the line \[\frac{x+2}{3}=\frac{2y+3}{4}=\frac{3z+4}{5}\] measured parallel to the plane \[4x+12y-3z+1=0.\] |
View Answer play_arrow
-
Using integration, find the area of the following region. \[\{(x,\,\,y):|x-1|\,\,\le \,y\le \sqrt{5-{{x}^{2}}}\}\]
View Answer play_arrow
-
| Find the volume of the largest cylinder that can be inscribed in sphere of radius r. |
| OR |
| A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that total surface area is minimum, the ratio of length of cylinder to the diameter of its semicircular ends is \[\pi :(\pi +2).\] |
View Answer play_arrow
-
If \[x+y+z=0,\]prove that