question_answer

Find the volume of the largest cylinder that can be inscribed in sphere of radius r.

OR

A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that total surface area is minimum, the ratio of length of cylinder to the diameter of its semicircular ends is \[\pi :(\pi +2).\]

Answer:

Given, r is the radius of sphere.

Let R be the radius, h be the height of cylinder and

V be the volume of the cylinder.

Then,                \[V=\pi {{R}^{2}}h\]                  ?(i)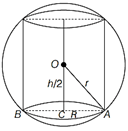

In right angled \[\Delta \,OAC,\]we have

\[{{r}^{2}}={{R}^{2}}+{{\left( \frac{h}{2} \right)}^{2}}\]

\[\Rightarrow \]               \[{{R}^{2}}={{r}^{2}}-\frac{{{h}^{2}}}{4}\]

\[\therefore \]                  \[V=\pi {{r}^{2}}h-\frac{\pi {{h}^{3}}}{4}\]

\[\therefore \]                  \[\frac{dV}{dh}=\pi {{r}^{2}}-\frac{3\pi {{h}^{2}}}{4}\]

Now,                 \[\frac{{{d}^{2}}V}{d{{h}^{2}}}=0-\frac{6\pi h}{4}=\frac{-\,3\pi h}{2}\]

For maximum or minimum value of V, put

\[\frac{dV}{dh}=0\]

\[\Rightarrow \]   \[\pi {{r}^{2}}-\frac{3\pi {{h}^{2}}}{4}=0\Rightarrow h=\frac{2}{\sqrt{3}}r\]

Now, \[{{\left( \frac{{{d}^{2}}V}{d{{h}^{2}}} \right)}_{h=\frac{2}{\sqrt{3}}r}}=\frac{-\,3\pi }{2}\times \frac{2}{\sqrt{3}}r=-\,\sqrt{3}\pi r<0\]

Thus, V is maximum when\[h=\frac{2}{\sqrt{3}}r\].

\[\therefore \]R is calculated as

\[{{R}^{2}}={{r}^{2}}-\frac{{{h}^{2}}}{4}\]

\[\Rightarrow \]               \[{{R}^{2}}={{r}^{2}}-\frac{1}{4}\times {{\left( \frac{2}{\sqrt{3}}r \right)}^{2}}=\sqrt{\frac{2}{3}}r\]

\[\therefore \]Maximum volume of the cylinder is given by

\[{{V}_{\max }}=\pi {{R}^{2}}h=\pi {{\left( \sqrt{\frac{2}{3}}r \right)}^{2}}\left( \frac{2}{\sqrt{3}}r \right)=\frac{4\pi {{r}^{3}}}{3\sqrt{3}}cu\,\,units\]

OR

Let r be radius of semicircular end and h be the height of the half cylinder.

Volume of half cylinder,\[V=\frac{1}{2}\pi {{r}^{2}}h;\]    ?(i)

Total surface area, \[S=\pi rh+\pi {{r}^{2}}+2rh\]

\[S=(\pi +2)\,r\cdot \frac{2V}{\pi {{r}^{2}}}+\pi {{r}^{2}}=\frac{2V\,(\pi +2)}{\pi r}+\pi {{r}^{2}}\] [from Eq. (i)]

\[\frac{dS}{dr}=\frac{-\,2V\,(\pi +2)}{\pi {{r}^{2}}}+2\pi r\]                               ?(ii)

For minimum or minimum surface area, put \[\frac{dS}{dr}=0\]

\[\Rightarrow \]               \[\frac{2V\,(\pi +2)}{\pi {{r}^{2}}}=2\pi r\]       ?(iii)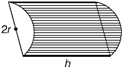

\[\frac{{{d}^{2}}S}{d{{r}^{2}}}=\frac{4V\,(\pi +2)}{\pi {{r}^{3}}}+2\pi >0\]for \[{{r}^{3}}=\frac{2V\,(\pi +2)}{2{{\pi }^{2}}}\] [from Eq. (iii)]

\[\therefore \]S is minimum for \[\frac{V\,(\pi +2)}{\pi {{r}^{2}}}=\pi r\]       [from Eq. (iii)]

\[\Rightarrow \]               \[\frac{\frac{1}{2}\pi {{r}^{2}}h\,(\pi +2)}{\pi {{r}^{2}}}=\pi r\]    [from Eq. (i)]

\[\Rightarrow \]               \[\frac{h}{2r}=\frac{\pi }{\pi +2}\Rightarrow h:2r=\pi :\pi +2\]

Hence proved.