question_answer

Using integration, find the area of the following region. \[\{(x,\,\,y):|x-1|\,\,\le \,y\le \sqrt{5-{{x}^{2}}}\}\]

Answer:

Given region is \[\{(x,\,\,y):|x-1|\le y\le \sqrt{5-{{x}^{2}}}\}\] Above region has two equations \[y=\,|x-1|\]and \[y=\sqrt{5-{{x}^{2}}}\] Now, we know that, \[|x|\,\,=\left\{ \begin{align}   & \,\,\,\,x,\,\,\,if\,\,x\ge 0 \\  & -\,x,\,\,\,if\,\,x<0 \\ \end{align} \right.\] Using above definition of modulus functions, we write \[y=\,\,|x-1|\,\,=\left\{ \begin{align}   & \,\,\,\,\,\,x-1,\,\,\,if\,\,x-1\ge 0 \\  & -\,(x-1),\,\,\,if\,\,x-1<0 \\ \end{align} \right.\] \[y=\left\{ \begin{align}   & x-1,\,\,\,if\,\,x\ge 1 \\  & 1-x,\,\,\,if\,\,x<1 \\ \end{align} \right.\] Also, other equation is\[y=\sqrt{5-{{x}^{2}}}\] On squaring both sides, we get \[{{y}^{2}}=5-{{x}^{2}}\Rightarrow {{x}^{2}}+{{y}^{2}}=5\] It is a circle with centre (0, 0) and radius, \[r=\sqrt{5}\]. On drawing the rough sketch, we get the following graph 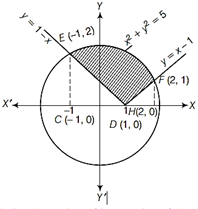For finding the points of intersection of the curves, we have \[y=1-x\]    ?(i) \[y=x-1\]             ?(ii) and \[{{x}^{2}}+{{y}^{2}}=5\] On putting \[y=1-x\]from Eq. (i) in Eq. (iii), we get \[{{x}^{2}}+{{(1-x)}^{2}}=5\] \[\Rightarrow \]   \[{{x}^{2}}+1+{{x}^{2}}-2x=5\] \[\Rightarrow \]   \[2{{x}^{2}}-2x-4=0\] \[\Rightarrow \]   \[{{x}^{2}}-x-2=0\] \[\Rightarrow \]   \[{{x}^{2}}-2x+x-2=0\] \[\Rightarrow \]\[x\,(x-2)+1\,(x-2)=0\] \[\Rightarrow \]   \[(x+1)\,(x-2)=0\] \[\therefore \]                  \[x=-\,1\]or 2 Now, when\[x=-\,1\], then \[{{y}^{2}}=5-{{x}^{2}}=5-1=4\] \[\Rightarrow \]               \[{{y}^{2}}=4\]          \[\Rightarrow \]\[y=\pm \,\,2\] and when \[x=2\], then \[{{y}^{2}}=5-{{x}^{2}}=5-4=1\] \[\Rightarrow \]               \[{{y}^{2}}=1\] \[\Rightarrow \]               \[y=\pm \,\,1\] So, points of intersection of Eqs. (i) and (ii) are \[(-\,1,\,\,\pm \,\,2)\]and \[(2,\,\,\pm \,\,1)\]. Now, putting \[y=x-1\]from Eq. (ii) in Eq. (iii), we get \[{{x}^{2}}+{{(x-1)}^{2}}=5\]\[\Rightarrow \]\[{{x}^{2}}+{{x}^{2}}+1-2x=5\] \[\Rightarrow \]\[2{{x}^{2}}-2x-4=0\]\[\Rightarrow \]\[{{x}^{2}}-x-2=0\] \[\Rightarrow \]\[(x-2)\,(x+1)=0\]\[\Rightarrow \]\[x=-\,1\]or 2 From Eq. (iii), at\[x=-\,1\], \[y=\pm 2\]and \[x=2,\]\[y=\pm 1\]Hence, the two curves intersect at\[(-\,1,\,\,\pm \,\,2)\]and \[(2,\,\,\pm \,\,1)\]. Now, required area \[\int_{-\,1}^{2}{{{y}_{(\,\,circle\,\,)}}dx-\int_{-\,1}^{1}{(y=1-x)\,dx-\int_{1}^{2}{(y=x-1)\,dx}}}\] \[=\int_{-\,1}^{2}{\sqrt{5-{{x}^{2}}}dx-}\int_{-\,1}^{1}{(1-x)\,dx-\int_{1}^{2}{(x-1)\,dx}}\] \[\left[ \because \int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}=\frac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\frac{{{a}^{2}}}{2}{{\sin }^{-\,1}}\frac{x}{a} \right]\] \[=\left[ \frac{x}{2}\sqrt{5-{{x}^{2}}}+\frac{5}{2}{{\sin }^{-\,1}}\frac{x}{\sqrt{5}} \right]_{-\,1}^{2}-\left[ x-\frac{{{x}^{2}}}{2} \right]_{-\,1}^{1}-\left[ \frac{{{x}^{2}}}{2}-x \right]_{1}^{2}\]\[=\left[ \left( \frac{2}{5}\sqrt{5-4}+\frac{5}{2}{{\sin }^{-\,1}}\frac{2}{\sqrt{5}} \right) \right]\] \[\left. -\left\{ -\frac{1}{2}\sqrt{4}+\frac{5}{2}{{\sin }^{-\,1}}\left( -\frac{1}{\sqrt{5}} \right) \right\} \right]\] \[-\,\left[ \left( 1-\frac{1}{2} \right)-\left( -1-\frac{1}{2} \right) \right]-\left[ \left( \frac{4}{2}-2 \right)-\left( \frac{1}{2}-1 \right) \right]\] \[=1+\frac{5}{2}{{\sin }^{-1}}\frac{2}{\sqrt{5}}+\frac{1}{2}\times 2-\frac{5}{2}{{\sin }^{-\,1}}\left( -\frac{1}{\sqrt{5}} \right)\] \[-\left( \frac{1}{2}+\frac{3}{2} \right)-\left( 0+\frac{1}{2} \right)\] \[=1+\frac{5}{2}{{\sin }^{-1}}\frac{2}{\sqrt{5}}+1+\frac{5}{2}{{\sin }^{-\,1}}\frac{1}{\sqrt{5}}-2-\frac{1}{2}\] \[[\because {{\sin }^{-\,1}}(-\,\theta )=-{{\sin }^{-\,1}}\theta ]\] \[=-\frac{1}{2}+\frac{5}{2}\left( {{\sin }^{-\,1}}\frac{2}{\sqrt{5}}+{{\sin }^{-\,1}}\frac{1}{\sqrt{5}} \right)\] \[=\left[ \frac{5}{2}\left( {{\sin }^{-1}}\frac{2}{\sqrt{5}}+{{\sin }^{-\,1}}\frac{1}{\sqrt{5}} \right)-\frac{1}{2} \right]\] \[=\frac{5}{2}\left[ {{\cos }^{-\,1}}\frac{1}{\sqrt{5}}+{{\sin }^{-\,1}}\frac{1}{\sqrt{5}} \right]-\frac{1}{2}\] \[\left[ \because {{\sin }^{-\,1}}\frac{2}{\sqrt{5}}={{\cos }^{-\,1}}\frac{1}{\sqrt{5}} \right]\] \[\frac{5}{2}\times \frac{\pi }{2}-\frac{1}{2}=\frac{1}{4}(5\pi -2)\] sq units