question_answer

If \[A({{x}_{1}},\,\,{{y}_{1}}),\] \[B({{x}_{2}},\,\,{{y}_{2}})\] and \[C({{x}_{3}},\,\,{{y}_{3}})\] are vertices of an equilateral triangle whose each side is equal to a, then prove that

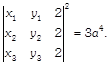
Answer:

Given, \[A\,({{x}_{1}},\,\,{{y}_{1}}),\] \[B\,({{x}_{2}},\,\,{{y}_{2}})\] and \[C\,({{x}_{3}},\,\,{{y}_{3}})\]are vertices of an equilateral triangle and each side of equilateral triangle = a Now, LHS = 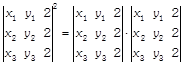By taking common 2 from \[{{C}_{3}}\] in both the determinant, we get 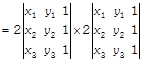\[=4\times (2\times Area\,\,of\,\,equilateral\,\,\Delta ABC)\] \[\times \,(2\times \text{Area}\,\,\text{of}\,\,\text{equilateral}\,\,\Delta ABC)\] [\[\because \]area of triangle whose vertices are \[({{x}_{1}},\,\,{{y}_{1}}),\,\,({{x}_{2}},\,\,{{y}_{2}})\]and 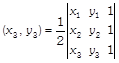\[=4\times 4\times {{[Area\,\,of\,\,equilateral\,\,\Delta \,ABC]}^{2}}\] \[=16\times {{\left[ \frac{\sqrt{3}}{4}\times {{a}^{2}} \right]}^{2}}\] \[=16\times \frac{3}{16}\times {{a}^{4}}\] [\[\because \]area of equilateral triangle\[=\frac{\sqrt{3}}{4}{{(side)}^{2}}\]] \[=3{{a}^{4}}=RHS\]             Hence proved.