question_answer

If a young man rides his motor-cycle at 25 km per hour, he had to spend Rs. 2 per km on petrol with very little pollution in the air. If he rides if at a faster speed of 40 km per hour, the petrol cost increases to Rs. 5 per km and rate of pollution also increases. He has Rs. 100 to spend on petrol and wishes to find what is the maximum distance he can travel within one hour. Express this problem as an LPP Solve it graphically to find the distance to be covered with different speeds. What value is indicated in this question?

Answer:

Let the young man drives x km and y km at 25 km/h and 40 km/h speed respectively, then LPP is maximise distance \[Z=x+y\] Subject to the constraints \[2x+5y\le 100\] \[\frac{x}{25}+\frac{y}{40}\le 1\]or \[8x+5y\le 200\] and \[x,\,\,y\ge 0\] 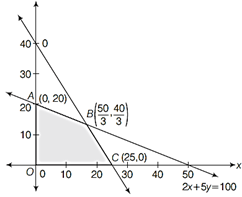The feasible region of the LPP is shaded in figure. The coordinates of the corner-points of the feasible region OABC are O (0, 0), A (0, 20), \[B\,\left( \frac{50}{3},\,\,\frac{40}{3} \right)\] and C (25, 0).

Corner Point	Value of Z
\[A\,(0,\,\,20)\]	20
\[B\left( \frac{50}{3},\,\,\frac{40}{3} \right)\]	30 (maximum)
\[C\,(25,\,\,0)\]	25

\[\therefore \]Maximum distance covered is 30 km with\[\frac{50}{3}\,km\] at 25 km/h speeds respectively. Value Vehicle should be driven at a moderate speed to decrease the pollution.