question_answer

Find the coordinates of point on line \[\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{6},\] which are at a distance of 3 units from the point  \[(1,\,\,-2,\,\,3).\]

OR

Show that the lines \[\vec{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda (3\hat{i}-\hat{j})\] and \[\vec{r}-=(4\hat{i}-\hat{k})+\mu (2\hat{i}+3\hat{k})\] are coplanar. Also, find the equation of the plane containing them.

Answer:

Let \[\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{6}=\lambda \]

Then, arbitrary point on the line is \[(2\lambda +1,\,\,3\lambda -2,\,\,6\lambda +3)\]

Suppose \[P\,(2\lambda +1,\,\,3\lambda -2,\,\,6\lambda +3)\] be the point at a distance 3 units from the point \[Q\,(1,\,\,-2,\,\,3)\]

\[\therefore \]                              \[PQ=3\]

\[{{(PQ)}^{2}}={{(3)}^{2}}=9\]

\[\Rightarrow \]\[{{(2\lambda +1-1)}^{2}}+{{(3\lambda -2+2)}^{2}}+{{(6\lambda +3-3)}^{2}}=9\]

\[\Rightarrow \]   \[{{(2\lambda )}^{2}}+{{(3\lambda )}^{2}}+{{(6\lambda )}^{2}}=9\Rightarrow 49{{\lambda }^{2}}=9\]

\[\Rightarrow \]               \[{{\lambda }^{2}}=\frac{9}{49}\]

\[\Rightarrow \]               \[\lambda =\pm \frac{3}{7}\]

\[\therefore \]Points are \[\left( 2\left( \frac{3}{7} \right)+1,\,\,3\left( \frac{3}{7} \right)-2,\,\,6\left( \frac{3}{7} \right)+3 \right)\]

\[\left( 2\left( \frac{-\,3}{7} \right)+1,\,\,3\left( \frac{-\,3}{7} \right)-2,\,\,6\left( \frac{-\,3}{7} \right)+3 \right)\]

\[=\left( \frac{13}{7},\,\,\frac{-\,5}{7},\,\,\frac{39}{7} \right)\] or \[\left( \frac{1}{7},\,\,\frac{-\,23}{7},\,\,\frac{3}{7} \right)\]

OR

Given lines are \[\overrightarrow{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda \,(3\,\hat{i}-\hat{j})\]

and                   \[\overrightarrow{r}=(4\,\hat{i}-\hat{k})+\mu \,(2\,\hat{i}+3\hat{k})\]

On comparing both equations of lines with \[\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}\]respectively, we get

\[\overrightarrow{{{a}_{1}}}=\hat{i}+\hat{j}-\hat{k},\,\,\overrightarrow{{{b}_{1}}}=3\hat{i}-\hat{j}\]

And      \[\overrightarrow{{{a}_{2}}}=4\,\hat{i}-\hat{k},\,\,\overrightarrow{{{b}_{2}}}=2\hat{i}+3\hat{k}\]

\[\therefore \]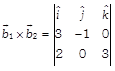

\[=\hat{i}\,(-\,3-0)-\hat{j}\,(9-0)+\hat{k}\,(0+2)\]

\[=-\,3\,\hat{i}-9\hat{j}+2\hat{k}\]

and \[{{\overrightarrow{a}}_{2}}-{{\overrightarrow{a}}_{1}}=(4\hat{i}-\hat{k})-(\hat{i}+\hat{j}-\hat{k})=3\hat{i}-\hat{j}\]

Now, \[({{\overrightarrow{a}}_{2}}-{{\overrightarrow{a}}_{1}})\cdot ({{\overrightarrow{b}}_{1}}\times {{\overrightarrow{b}}_{2}})=(3\,\hat{i}-\hat{j})\cdot (-\,3\,\hat{i}-9\hat{j}+2\hat{k})\]

\[=-\,9+9=0\]

Hence, the given lines are coplanar.

Now, Cartesian equations of given lines are

\[\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}\]and \[\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}\].

Then, equation of plane containing them is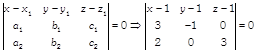

\Rightarrow \left| \begin{matrix}    x-1 & y-1 & z-1  \\    3 & -1 & 0  \\    2 & 0 & 3  \\ \end{matrix} \right|=0\]\[\Rightarrow \]\[(x-1)(-3-0)-(y-1)(9-0)+(z+1)(0+2)=0\]

\[\Rightarrow \]               \[-\,3x+3-9y+9+2z+2=0\]

\[\therefore \]                              \[3x+9y-2z=14\]