(1) The simple gas laws relating gas volume to pressure, temperature and amount of gas, respectively, are stated below:
Boyle's law : \[P\propto \frac{1}{V}\] or \[V\propto \frac{1}{P}\] (n and T constant)
Charle's law : \[V\propto \text{T}\] (n and P constant)
Avogadro's law : \[V\propto n\] (T and P constant)
If all the above law's combines, then
\[V\propto \frac{nT}{P}\]
or \[V=\frac{nRT}{P}\] (\[R=\] Ideal gas constant)
or \[PV=nRT\]
This is called ideal gas equation. R is called ideal gas constant. This equation is obeyed by isothermal and adiabatic processes.
(2) Nature and values of R : From the ideal gas equation, \[R=\frac{PV}{nT}=\frac{\text{Pressure}\times \text{Volume}}{\text{mole}\times \text{Temperature}}\]
\[=\frac{\frac{\text{Force}}{\text{Area}}\times \text{Volume}}{\text{mole}\times \text{Temperature}}=\frac{\text{Force}\times \text{Length}}{\text{mole}\times \text{Temperature}}\]
\[=\frac{\text{Work or energy}}{\text{mole}\times \text{Temperature}}\].
R is expressed in the unit of work or energy \[mo{{l}^{-1}}\,{{K}^{-1}}\].
Since different values of R are summarised below :
\[R=0.0821\,L\,atm\,mo{{l}^{-1}}\,{{K}^{-1}}\]
\[=8.3143\,joule\,mo{{l}^{-1}}\,{{K}^{-1}}\] (S.I. unit)
\[=8.3143\,Nm\,mo{{l}^{-1}}\,{{K}^{-1}}\]
\[=8.3143\,KPa\,d{{m}^{3}}\,mo{{l}^{-1}}\,{{K}^{-1}}\]
\[=8.3143\,MPa\,c{{m}^{3}}\,mo{{l}^{-1}}\,{{K}^{-1}}\]
\[=5.189\times {{10}^{19}}\,eV\,mo{{l}^{-1}}\,{{K}^{-1}}\]
\[=1.99\,cal\,mo{{l}^{-1}}\,{{K}^{-1}}\]
(3) Gas constant, R for a single molecule is called Boltzmann constant (k)
\[k=\frac{R}{N}=\frac{8.314\times {{10}^{7}}}{6.023\times {{10}^{23}}}ergs\,mol{{e}^{-1}}\,degre{{e}^{-1}}\]
\[=1.38\times {{10}^{-16}}ergs\,mo{{l}^{-1}}\,degre{{e}^{-1}}\]
or \[1.38\times {{10}^{-23}}\,joule\,mo{{l}^{-1}}\,degre{{e}^{-1}}\]
(4) Calculation of mass, molecular weight and density of the gas by gas equation
\[PV=nRT=\frac{m}{M}RT\] \[\left( \because n=\frac{\text{mass of the gas (}m\text{)}}{\text{Molecular weight of the gas (}M\text{)}} \right)\]
\[M=\frac{mRT}{PV}\]
\[d=\frac{PM}{RT}\] \[\left( \because d=\frac{m}{V} \right)\]
or \[\frac{dT}{P}=\frac{M}{R}\], \[\frac{M}{R}=\] Constant
(\[\because \] M and R are constant for a particular gas)
Thus, \[\frac{dT}{P}\] or \[\frac{{{d}_{1}}{{T}_{1}}}{{{P}_{1}}}=\frac{{{d}_{2}}{{T}_{2}}}{{{T}_{2}}}\]= Constant
(For two or more different temperature and pressure)
(5) Gas densities differ from those of solids and liquids as,
(i) Gas densities are generally stated in g/L instead of \[g/c{{m}^{3}}\].
(ii) Gas densities are strongly dependent on pressure and temperature as, \[d\propto P\]\[\propto 1/T\]
Densities of liquids and solids, do depend somewhat on temperature, but they are far less dependent on pressure.
(iii) The density of a gas is directly proportional to its molar mass. No simple relationship exists between the density and molar mass for liquid and solids.
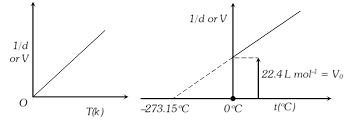
(iv) Density of a gas at STP \[=\frac{\text{molar mass}}{22.4}\]
\[d({{N}_{2}})\] at STP\[=\frac{28}{22.4}=1.25\,g\,{{L}^{-1}}\],
\[d({{O}_{2}})\] at STP \[=\frac{32}{22.4}=1.43\,g\,{{L}^{-1}}\]
 (2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\]
where n is the number of molecules per unit molar volume,
\[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by,
\[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]
where, \[{{\sigma }_{AB}}=\frac{{{\sigma }_{A}}+{{\sigma }_{B}}}{2}\]
\[{{M}_{A}}\], \[{{M}_{B}}\] are molecular weights \[(M=m{{N}_{0}})\]
(iv) (a) At particular temperature; \[Z\propto {{p}^{2}}\]
(b) At particular pressure; \[Z\propto {{T}^{-3/2}}\]
(c) At particular volume; \[Z\propto {{T}^{1/2}}\]
(3) During molecular collisions a molecule covers a small distance before it gets deflected. The average distance travelled by the gas molecules between two successive collision is called mean free path (l).
\[\lambda =\frac{\text{Average distance travelled per unit time(}{{u}_{\text{av}}}\text{)}}{\text{No}\text{. of collisions made by single molecule per unit time (}{{Z}_{A}}\text{)}}\].
\[=\frac{{{u}_{\text{av}}}}{\sqrt{\text{2}}\pi {{\sigma }^{2}}{{u}_{\text{avr}\text{.}}}n}=\frac{1}{\sqrt{2}\pi n{{\sigma }^{2}}}\]
(4) Based on kinetic theory of gases mean free path, \[\lambda \propto \frac{T}{P}\]. Thus,
(i) Larger the size of the molecules, smaller the mean free path, i.e., \[\lambda \propto \frac{1}{{{\text{(radius)}}^{\text{2}}}}\]
(ii) Greater the number of molecules per unit volume, smaller the mean free path.
(iii) Larger the temperature, larger the mean free path.
(iv) Larger the pressure, smaller the mean free path.
(5) Relation between collision frequency (Z) and mean free path (l) is given by, \[Z=\frac{{{u}_{rms}}}{\lambda }\]
(2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\]
where n is the number of molecules per unit molar volume,
\[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by,
\[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]
where, \[{{\sigma }_{AB}}=\frac{{{\sigma }_{A}}+{{\sigma }_{B}}}{2}\]
\[{{M}_{A}}\], \[{{M}_{B}}\] are molecular weights \[(M=m{{N}_{0}})\]
(iv) (a) At particular temperature; \[Z\propto {{p}^{2}}\]
(b) At particular pressure; \[Z\propto {{T}^{-3/2}}\]
(c) At particular volume; \[Z\propto {{T}^{1/2}}\]
(3) During molecular collisions a molecule covers a small distance before it gets deflected. The average distance travelled by the gas molecules between two successive collision is called mean free path (l).
\[\lambda =\frac{\text{Average distance travelled per unit time(}{{u}_{\text{av}}}\text{)}}{\text{No}\text{. of collisions made by single molecule per unit time (}{{Z}_{A}}\text{)}}\].
\[=\frac{{{u}_{\text{av}}}}{\sqrt{\text{2}}\pi {{\sigma }^{2}}{{u}_{\text{avr}\text{.}}}n}=\frac{1}{\sqrt{2}\pi n{{\sigma }^{2}}}\]
(4) Based on kinetic theory of gases mean free path, \[\lambda \propto \frac{T}{P}\]. Thus,
(i) Larger the size of the molecules, smaller the mean free path, i.e., \[\lambda \propto \frac{1}{{{\text{(radius)}}^{\text{2}}}}\]
(ii) Greater the number of molecules per unit volume, smaller the mean free path.
(iii) Larger the temperature, larger the mean free path.
(iv) Larger the pressure, smaller the mean free path.
(5) Relation between collision frequency (Z) and mean free path (l) is given by, \[Z=\frac{{{u}_{rms}}}{\lambda }\] 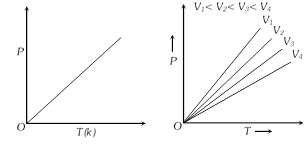
 (5) At constant mass and pressure density of a gas is inversely proportional to it absolute temperature.
Thus, \[d\propto \frac{1}{T}\propto \frac{1}{V}\] \[\left[ \because V=\frac{\text{mass}}{\text{d}} \right]\]
or \[\frac{{{d}_{1}}}{{{d}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{V}_{1}}}=......=K\] (6) Use of hot air balloons in sports and meteorological observations is an application of Charle's law.
(5) At constant mass and pressure density of a gas is inversely proportional to it absolute temperature.
Thus, \[d\propto \frac{1}{T}\propto \frac{1}{V}\] \[\left[ \because V=\frac{\text{mass}}{\text{d}} \right]\]
or \[\frac{{{d}_{1}}}{{{d}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{{{V}_{2}}}{{{V}_{1}}}=......=K\] (6) Use of hot air balloons in sports and meteorological observations is an application of Charle's law. 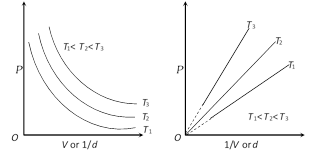
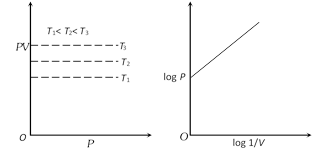 (4) At constant mass and temperature density of a gas is directly proportional to its pressure and inversely proportional to its volume.
Thus, \[d\propto P\propto \frac{1}{V}\]
\[\left[ \because V=\frac{\text{mass}}{d} \right]\]
or \[\frac{{{d}_{1}}}{{{d}_{2}}}=\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{{{V}_{2}}}{{{V}_{1}}}=.......=K\]
(5) At altitudes, as P is low d of air is less. That is why mountaineers carry oxygen cylinders.
(4) At constant mass and temperature density of a gas is directly proportional to its pressure and inversely proportional to its volume.
Thus, \[d\propto P\propto \frac{1}{V}\]
\[\left[ \because V=\frac{\text{mass}}{d} \right]\]
or \[\frac{{{d}_{1}}}{{{d}_{2}}}=\frac{{{P}_{1}}}{{{P}_{2}}}=\frac{{{V}_{2}}}{{{V}_{1}}}=.......=K\]
(5) At altitudes, as P is low d of air is less. That is why mountaineers carry oxygen cylinders.