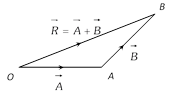
 (1) Magnitude of resultant vector
In \[\Delta \,ABN,\]\[\cos \theta =\frac{AN}{B}\]\[\therefore \]\[AN=B\cos \theta \]
\[\sin \theta =\frac{BN}{B}\] \[\therefore \] \[BN=B\sin \theta \]
In \[\Delta OBN,\] we have \[O{{B}^{2}}=O{{N}^{2}}+B{{N}^{2}}\]
(1) Magnitude of resultant vector
In \[\Delta \,ABN,\]\[\cos \theta =\frac{AN}{B}\]\[\therefore \]\[AN=B\cos \theta \]
\[\sin \theta =\frac{BN}{B}\] \[\therefore \] \[BN=B\sin \theta \]
In \[\Delta OBN,\] we have \[O{{B}^{2}}=O{{N}^{2}}+B{{N}^{2}}\]
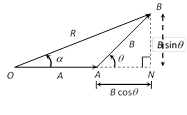 \[\Rightarrow \]\[{{R}^{2}}={{(A+B\cos \theta )}^{2}}+{{(B\sin \theta )}^{2}}\]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}{{\cos }^{2}}\theta +2AB\cos \theta +{{B}^{2}}{{\sin }^{2}}\theta \]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}({{\cos }^{2}}\theta +{{\sin }^{2}}\theta )+2AB\cos \theta \]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}+2AB\cos \theta \] \[\Rightarrow \]
\[R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\]
(2) Direction of resultant vectors : If \[\theta \] is angle between \[\overrightarrow{A}\] and \[\overrightarrow{B,}\] then
\[\,|\overrightarrow{A}+\overrightarrow{B}|\,=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\]
If \[\overrightarrow{R}\]makes an angle a with \[\overrightarrow{A},\] then in \[\Delta OBN,\]
\[\tan \alpha =\frac{BN}{ON}=\frac{BN}{OA+AN}\]
\[\tan \alpha =\frac{B\sin \theta }{A+B\cos \theta }\]
\[\Rightarrow \]\[{{R}^{2}}={{(A+B\cos \theta )}^{2}}+{{(B\sin \theta )}^{2}}\]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}{{\cos }^{2}}\theta +2AB\cos \theta +{{B}^{2}}{{\sin }^{2}}\theta \]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}({{\cos }^{2}}\theta +{{\sin }^{2}}\theta )+2AB\cos \theta \]
\[\Rightarrow \]\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}+2AB\cos \theta \] \[\Rightarrow \]
\[R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\]
(2) Direction of resultant vectors : If \[\theta \] is angle between \[\overrightarrow{A}\] and \[\overrightarrow{B,}\] then
\[\,|\overrightarrow{A}+\overrightarrow{B}|\,=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\]
If \[\overrightarrow{R}\]makes an angle a with \[\overrightarrow{A},\] then in \[\Delta OBN,\]
\[\tan \alpha =\frac{BN}{ON}=\frac{BN}{OA+AN}\]
\[\tan \alpha =\frac{B\sin \theta }{A+B\cos \theta }\]
 (8) Polar vectors : These have starting point or point of application . Example displacement and force etc.
(9) Axial Vectors : These represent rotational effects and are always along the axis of rotation in accordance with right hand screw rule. Angular velocity, torque and angular momentum, etc., are example of physical quantities of this type.
(8) Polar vectors : These have starting point or point of application . Example displacement and force etc.
(9) Axial Vectors : These represent rotational effects and are always along the axis of rotation in accordance with right hand screw rule. Angular velocity, torque and angular momentum, etc., are example of physical quantities of this type.
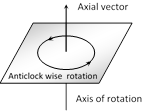
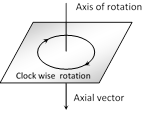 (10) Coplanar vector : Three (or more) vectors are called coplanar vector if they lie in the same plane. Two (free) vectors are always coplanar.
(10) Coplanar vector : Three (or more) vectors are called coplanar vector if they lie in the same plane. Two (free) vectors are always coplanar. 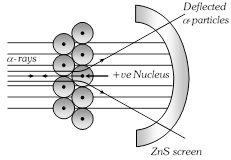 (2) From the above observations he concluded that, an atom consists of
(i) Nucleus which is small in size but carries the entire mass i.e. contains all the neutrons and protons.
(ii) Extra nuclear part which contains electrons. This model was similar to the solar system.
(3) Properties of the nucleus
(i) Nucleus is a small, heavy, positively charged portion of the atom and located at the centre of the atom.
(ii) All the positive charge of atom (i.e. protons) are present in nucleus.
(iii) Nucleus contains neutrons and protons, and hence these particles collectively are also referred to as nucleons.
(iv) The size of nucleus is measured in Fermi (1 Fermi = 10?13 cm).
(v) The radius of nucleus is of the order of \[1.5\times {{10}^{-13}}cm.\] to \[6.5\times {{10}^{-13}}cm.\] i.e. \[1.5\] to \[6.5\] Fermi. Generally the radius of the nucleus (\[{{r}_{n}})\] is given by the following relation,
\[{{r}_{n}}={{r}_{o}}(=1.4\times {{10}^{-13}}cm)\times {{A}^{1/3}}\]
This exhibited that nucleus is \[{{10}^{-5}}\] times small in size as compared to the total size of atom.
(vi) The Volume of the nucleus is about \[{{10}^{-39}}\]\[c{{m}^{3}}\] and that of atom is \[{{10}^{-24}}c{{m}^{3}},\] i.e., volume of the nucleus is \[{{10}^{-15}}\] times that of an atom.
(vii) The density of the nucleus is of the order of \[{{10}^{15}}g\,c{{m}^{-3}}\] or \[{{10}^{8}}\] tonnes \[c{{m}^{-3}}\] or \[{{10}^{12}}kg/cc\]. If nucleus is spherical than,
Density =\[\frac{\text{mass of the nucleus}}{\text{volume of the nucleus }}=\]\[\frac{\text{mass number}}{6.023\times {{10}^{23}}\times \frac{4}{3}\pi {{r}^{3}}}\]
(4) Drawbacks of Rutherford's model
(i) It does not obey the Maxwell theory of electrodynamics, according to it ?A small charged particle moving around an oppositely charged centre continuously loses its energy?. If an electron does so, it should also continuously lose its energy and should set up spiral motion ultimately failing into the nucleus.
(ii) It could not explain the line spectra of \[H-\] atom and discontinuous spectrum nature.
(2) From the above observations he concluded that, an atom consists of
(i) Nucleus which is small in size but carries the entire mass i.e. contains all the neutrons and protons.
(ii) Extra nuclear part which contains electrons. This model was similar to the solar system.
(3) Properties of the nucleus
(i) Nucleus is a small, heavy, positively charged portion of the atom and located at the centre of the atom.
(ii) All the positive charge of atom (i.e. protons) are present in nucleus.
(iii) Nucleus contains neutrons and protons, and hence these particles collectively are also referred to as nucleons.
(iv) The size of nucleus is measured in Fermi (1 Fermi = 10?13 cm).
(v) The radius of nucleus is of the order of \[1.5\times {{10}^{-13}}cm.\] to \[6.5\times {{10}^{-13}}cm.\] i.e. \[1.5\] to \[6.5\] Fermi. Generally the radius of the nucleus (\[{{r}_{n}})\] is given by the following relation,
\[{{r}_{n}}={{r}_{o}}(=1.4\times {{10}^{-13}}cm)\times {{A}^{1/3}}\]
This exhibited that nucleus is \[{{10}^{-5}}\] times small in size as compared to the total size of atom.
(vi) The Volume of the nucleus is about \[{{10}^{-39}}\]\[c{{m}^{3}}\] and that of atom is \[{{10}^{-24}}c{{m}^{3}},\] i.e., volume of the nucleus is \[{{10}^{-15}}\] times that of an atom.
(vii) The density of the nucleus is of the order of \[{{10}^{15}}g\,c{{m}^{-3}}\] or \[{{10}^{8}}\] tonnes \[c{{m}^{-3}}\] or \[{{10}^{12}}kg/cc\]. If nucleus is spherical than,
Density =\[\frac{\text{mass of the nucleus}}{\text{volume of the nucleus }}=\]\[\frac{\text{mass number}}{6.023\times {{10}^{23}}\times \frac{4}{3}\pi {{r}^{3}}}\]
(4) Drawbacks of Rutherford's model
(i) It does not obey the Maxwell theory of electrodynamics, according to it ?A small charged particle moving around an oppositely charged centre continuously loses its energy?. If an electron does so, it should also continuously lose its energy and should set up spiral motion ultimately failing into the nucleus.
(ii) It could not explain the line spectra of \[H-\] atom and discontinuous spectrum nature. You need to login to perform this action.
You will be redirected in
3 sec
