Category : 2nd Class
Division
Synopsis
Division:
e.g., In 20 \[\div \] 5 = 4, 20 is the dividend, 5 is the divisor and 4 is quotient when 20 is divided exactly by 5. So, remainder is 0.
|
Note : Unlike addition, subtraction and multiplication which are done from the right most digit (i.e., ones) division is done from the left most digit of the dividend. |
Step-1: 67 \[\div \] 4
Write the given division as shown.
Divisor \[\leftarrow \] ![]()
Step - 2: Starting from the left most digit, find the number of times the divisor is in the digit.
There is one 4 in 6.
Put this 1 in quotient and 4 below 6 as shown.
![]() Quotient
Quotient
Step - 3: Now, subtract 4 from 6 in the dividend and write the difference 2 below the
Separator line 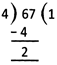
Step - 4: Bring down the next digit (ie., 7) beside 2 as shown.
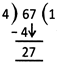
Find the number of 4's in the new dividend 27.
4 \[\times \] 6 = 24 and 4 \[\times \]7 = 28
So, there are 6 fours in the dividend 27. Write 6 beside 1 in the quotient and 24 below 27 as shown. Subtract 24 from 27 and write the difference 3 below the
separator line shown. 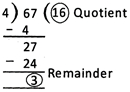
Step - 5: The number 3 < 4 and 4 cannot divide 3. So, 3 remains undivided and is called the remainder. Stop the division when the remainder is less than the divisor.
Therefore, in 67 \[\div \] 4:
67 is dividend; 4 is divisor; 16 is quotient and 3 is remainder.
40 \[\div \] 5 = 8 \[\to \] a) 40 = 5 \[\times \] 8 b) 40 = 8 \[\times \]5
5 \[\times \]8 = 40 \[\to \] a) 40 \[\div \] 5 = 8 b) 40 \[\div \]8 = 5
You need to login to perform this action.
You will be redirected in
3 sec
