-
Evaluate the determinant
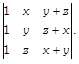
-
If a unit vector \[\hat{a}\] makes angles \[\frac{\pi }{3}\] with \[\hat{i},\,\,\frac{\pi }{4}\] with \[\hat{j}\] and an acute angle \[\gamma \] with \[\hat{k}\] find the value of \[\gamma .\]
View Answer play_arrow
-
Write the value of a for which \[f(x)=\left\{ \begin{matrix} 5x-4, & 0<x\le 1 \\ 4{{x}^{2}}+3ax, & 1<x<2 \\ \end{matrix} \right.\] is continuous at x = 1?
View Answer play_arrow
-
Evaluate \[\int_{0}^{2}{{{e}^{x-[x]}}dx.}\]
View Answer play_arrow
-
If \[{{x}^{m}}{{y}^{n}}={{(x+y)}^{m\,\,+\,\,n}},\] then prove that \[\frac{{{d}^{2}}y}{d{{x}^{2}}}=0.\]
View Answer play_arrow
-
If \[\vec{a},\] \[\vec{b}\] and \[\vec{c}\] are three non-coplanar vectors, prove that \[[\begin{matrix} \vec{a}+\vec{b}+\vec{c} & \vec{a}+\vec{b} & \vec{a}+\vec{c} \\ \end{matrix}]=-[\begin{matrix} {\vec{a}} & {\vec{b}} & {\vec{c}} \\ \end{matrix}].\]
View Answer play_arrow
-
If \[A=\left[ \begin{matrix} 3 & 5 \\ 7 & -\,9 \\ \end{matrix} \right]\] and \[B=\left[ \begin{matrix} 6 & -\,4 \\ 2 & 3 \\ \end{matrix} \right],\] find \[(4A-3B).\]
View Answer play_arrow
-
Show that the function \[y=Ax+\frac{B}{x}\] is a solution of the differential equation \[{{x}^{2}}\frac{{{d}^{2}}y}{d{{x}^{2}}}+x\frac{dy}{dx}-y=0.\]
View Answer play_arrow
-
An edge of a variable cube is increasing at the rate of 10 cm/s. How fast the volume of the cube is increasing when the edge is 5 cm long?
View Answer play_arrow
-
Find the approximate value of \[\sqrt{25.2.}\]
View Answer play_arrow
-
Evaluate \[\int_{-1}^{2}{(|x+1|+|x|+|x-1|)}\,dx\]
View Answer play_arrow
-
Find the binomial distribution for which the mean is 4 and variance 3.
View Answer play_arrow
-
If f(x) and g(x) are two functions derivable in [a, b], such that f(a) = 4, f(b) = 10, g(a) = 1 and g(b) = 3, show that for a<c<b, f?(c) = 3g?(c.)
View Answer play_arrow
-
For what value of k, is the function
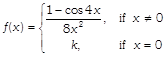
Continuous at x = 0?
-
Find the adjoint of the matrix
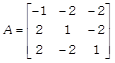
and hence show that A (adj A) \[=\,\,|A|{{I}_{3}}.\]
-
Prove that \[{{\tan }^{-1}}\left( \frac{a\cos x-b\sin x}{b\cos x-a\sin x} \right)={{\tan }^{-1}}\left( \frac{a}{b} \right)-x.\] Or Prove that \[{{\cot }^{-1}}\left[ \frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}} \right]=\frac{x}{2},\] \[x\in \left( 0,\,\,\frac{\pi }{4} \right).\]
View Answer play_arrow
-
Find the particular solution of the following differential equation : \[xy\frac{dy}{x}=(x+2)(y+2);y=-\,1,\] when x = 1. Or Find the particular solution of the following differential equation. \[x({{x}^{2}}-1)\frac{dy}{dx}=1;\] y = 0, when x = 2
View Answer play_arrow
-
Evaluate \[\int{\frac{dx}{{{\sin }^{4}}x+{{\cos }^{4}}x}.}\]
View Answer play_arrow
-
Evaluate \[\int_{0}^{\pi }{\frac{dx}{3+2\sin x+\cos x}.}\]
View Answer play_arrow
-
If \[\vec{a},\] \[\vec{b}\] and \[\vec{c}\] are three vectors, such that \[|\vec{a}|\,\,=5,\] \[|\vec{b}|\,\,=12,\] \[|\vec{c}|\,\,=13\]and \[\vec{a}+\vec{b}+\vec{c}=\vec{0}.\] find the value of \[\vec{a}\cdot \vec{b}+\vec{b}\cdot \vec{c}+\vec{c}\cdot \vec{a}\].
View Answer play_arrow
-
| Find the vector equation of the plane passing through the point \[(2,\,\,0,\,\,-\,1)\] and perpendicular to the line joining the points (1, 2, 3) and \[(3,\,\,-1,\,\,6).\] |
| OR |
| Find the equation of the line passing through the point (2, 1, 3) and perpendicular to the lines |
| \[\frac{x-1}{1}=\frac{y+1}{2}=\frac{z-2}{3}\] |
| and \[\frac{x-4}{-\,3}=\frac{y+1}{2}=\frac{z-1}{5}.\] |
View Answer play_arrow
-
In a box containing 100 bulbs, 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective? Write two advantages of using CFL (compact fluroscent lamp) bulbs over incandescent bulbs.
View Answer play_arrow
-
In a factory which manufactures bolts, machines A, B and C manufacture respectively 30%, 50% and 20% of the bolts. Out of their outputs 3%, 4% and 1%, respectively are defective bolts. A bolt is drawn at random from the product and is found to be defective. Find the probability that this is not manufactured by machine B.
View Answer play_arrow
-
| A binary operation \['*'\] is defined on the set |
| \[X=R-\{-\,1\}\] by \[x*y=x+y+xy,\] \[\forall x,\] \[y\in X.\] Check whether \['*'\] is commutative and associative. Find its identity element and also find the inverse of each element of X. |
| OR |
| If N denotes the set of all natural numbers and R be the relation on \[N\times N\] defined by (a, b)R |
| (c, d), if \[ad(b+c)=bc(a+d).\]Show that R is an equivalence relation. |
View Answer play_arrow
-
A manufacturer considers that men and women workers are equally efficient and so he pays them at the same rate. He has 30 and 17 units of workers (male and female) and capital respectively, which he uses to produce two types of goods A and B. To produce one unit of A, 2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce one unit of B. If A and B are priced at Rs. 100 and Rs. 120 per unit respectively, how should he use his resources to maximize the total revenue? Form the above as an LPP and solve graphically. What quality of manufacturer shown here.
View Answer play_arrow
-
Find the maximum area of an isosceles triangle inscribed in the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] with its vertex at one end of the major axis.
View Answer play_arrow
-
| Using integration, find the area of the triangular region whose vertices are |
| P (1, 0), Q (2, 2) and R (3, 1). |
| OR |
| Using integration find the area of the following region. |
| \[\{(x,\,\,y):|x-1|\,\,\le y\le \sqrt{5-{{x}^{2}}}\}\] |
View Answer play_arrow
-
| Find the vector equation of the plane passing through the three points with position vectors \[\hat{i}+\hat{j}-2\hat{k},\] \[2\hat{i}-\hat{j}+\hat{k}\] and \[\hat{i}+2\hat{j}+\hat{k}.\] Also, find the coordinates of the point of intersection of this plane and the line \[\vec{r}=(3\hat{i}-\hat{j}-\hat{k})+\lambda (2\hat{i}-2\hat{j}+\hat{k}).\] |
| OR |
| Find the vector equation of the plane through the points \[(2,\,\,1,\,\,-\,1)\] and \[(-\,1,\,\,3,\,\,4)\] and perpendicular to the plane \[x-2y+4z=10.\] |
View Answer play_arrow
-
If a, b and c are all distinct and
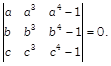
Show that \[abc(ab+bc+ca)=a+~b+c.\]
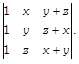
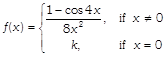 Continuous at x = 0?
Continuous at x = 0? 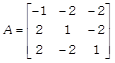 and hence show that A (adj A) \[=\,\,|A|{{I}_{3}}.\]
and hence show that A (adj A) \[=\,\,|A|{{I}_{3}}.\] 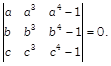 Show that \[abc(ab+bc+ca)=a+~b+c.\]
Show that \[abc(ab+bc+ca)=a+~b+c.\] 