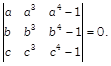question_answer

If a, b and c are all distinct and Show that \[abc(ab+bc+ca)=a+~b+c.\]

Answer:

Let 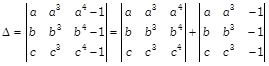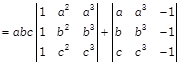[taking common a, b and c from \[{{R}_{1}},\]\[{{R}_{2}},\]and\[{{R}_{3}},\] respectively in first determinant] Applying\[{{R}_{2}}\to {{R}_{2}}-{{R}_{1}}\]and \[{{R}_{3}}\to {{R}_{3}}-{{R}_{1}},\] 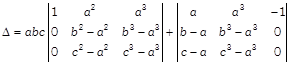Taking \[(b-a)\] and \[(c-a)\]common from \[{{R}_{2}}\]and \[{{R}_{3}}\]respectively in first and second determinant, we get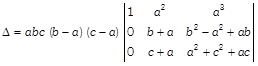 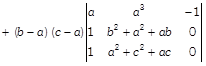Now, expand first determinant along \[{{C}_{1}}\] and expand second determinant along \[{{C}_{3}},\] we get Applying\[{{R}_{2}}\to {{R}_{2}}-{{R}_{1}}\]in both the determinant, we get \[\Delta =abc\,\,(b-a)\,\,(c-a)\left| \begin{matrix}    b+a & {{b}^{2}}+{{a}^{2}}+ab  \\    c-b & {{c}^{2}}-{{b}^{2}}+a\,(c-b)  \\ \end{matrix} \right|\] \[-\,(b-a)\,\,(c-a)\left| \begin{matrix}    1 & {{b}^{2}}+{{a}^{2}}+ab  \\    0 & {{c}^{2}}-{{b}^{2}}a\,(c-b)  \\ \end{matrix} \right|\] Taking \[(c-b)\] common from \[{{R}_{2}}\] in both the determinant, we get \[\Delta =abc\,\,(b-a)\,\,(c-a)\,\,(c-b)\left| \begin{matrix}    b+a & {{b}^{2}}+{{a}^{2}}+ab  \\    1 & a+b+c  \\ \end{matrix} \right|\] \[-\,(b-a)\,\,(c-a)\,\,(c-b)\left| \begin{matrix}    1 & {{b}^{2}}+{{a}^{2}}+ab  \\    0 & a+b+c  \\ \end{matrix} \right|\] \[=abc\,\,(b-a)\,\,(c-a)\,\,(c-b)\] \[[(a+b)\,\,(a+b+c)-({{b}^{2}}+{{a}^{2}}+ab)]\] \[-\,(b-a)\,\,(c-a)\,\,(c-b)\,\,[a+b+c]\] \[=abc\,\,(a-b)\,\,(b-c)\,\,(c-a)\,\,[{{a}^{2}}+ab+ac+ab]\] \[+{{b}^{2}}+bc-({{b}^{2}}+{{a}^{2}}+ab)\] \[-\,(a-b)\,\,(b-c)\,\,(c-a)\,\,(a+b+c)\] \[=abc\,(a-b)\,(b-c)\,\,(c-a)\,\,(ab+bc+ca)\] \[-\,(a-b)\,\,(b-c)\,\,(c-a)\,\,(a+b+c)\] \[=(a-b)\,\,(b-c)\,\,(c-a)\,\,[abc\,(ab+bc+ca)]\] \[-\,(a+b+c)]\] Now, \[\Delta =0\Rightarrow (a-b)\,\,(b-c)\,\,(c-a)\,\,[abc\,(ab+bc+ca\] \[-\,(a+b+c)]=0\] \[\Rightarrow \]\[abc\,\,(ab+bc+ca)-(a+b+c)=0\] \[[\because a\ne b,\,\,b\ne c,\,\,c\ne a\therefore a-b\ne 0,\] \[b-c\ne 0,\,\,c-a\ne 0]\] \[\Rightarrow \]   x