question_answer

Find the maximum area of an isosceles triangle inscribed in the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] with its vertex at one end of the major axis.

Answer:

Let the equation of an ellipse be \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1,\]then any point P on the ellipse is \[(a\cos \theta ,\,\,b\sin \theta )\]. From P, draw \[PM\bot OX\] and produce it to meet the ellipse at Q, then APQ is an isosceles triangle, let S be its area, Then \[S=2\times \frac{1}{2}\times AM\times MP=(OA-OM)\times MP\] \[=(a-a\cos \theta )\cdot b\sin \theta \] \[\Rightarrow \] \[S=ab\,\,(\sin \theta -\sin \theta \cos \theta )=ab\left( \sin \theta -\frac{1}{2} \right)\sin 2\theta \] 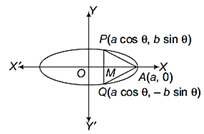On differentiating w.r.t. q, we get \[\frac{dS}{d\theta }=ab\,\,(cos\theta -cos2\theta )\] Again differentiating w.r.t. q, we get \[\frac{{{d}^{2}}S}{d{{\theta }^{2}}}=ab\,\,(-\,\sin \theta +2\sin 2\theta )\] For maxima or minima, put\[\frac{dS}{d\theta }=0\] \[\Rightarrow \]   \[\cos \theta =\cos 2\theta \Rightarrow 2\theta =2\pi -\theta \] \[\Rightarrow \]               \[\theta =\frac{2\pi}{3}\] At \[\theta =\frac{2\pi }{3},\,\,{{\left( \frac{{{d}^{2}}S}{d{{\theta }^{2}}} \right)}_{\theta =\frac{2\pi }{3}}}=ab\,\,\left[ -\,\sin \frac{2\pi }{3}+2\sin \,\,\left( 2\times \frac{2\pi }{3} \right) \right]\]\[=ab\left[ -\,\sin \left( \pi -\frac{\pi }{3} \right)+2\sin \left( \pi +\frac{\pi }{3} \right) \right]\] \[=ab\left( -\,\sin \frac{\pi }{3}-2\sin \frac{\pi }{3} \right)\]  \[\left[ \begin{align}   & \because \sin \left( \pi -\frac{\pi }{3} \right)=\sin \frac{\pi }{3}, \\  & \sin \left( \pi +\frac{\pi }{3} \right)=\frac{-\,\sin \pi }{3} \\ \end{align} \right]\] \[=ab\,\left( -\frac{\sqrt{3}}{2}-\frac{2\sqrt{3}}{2} \right)=ab\,\left( \frac{-\,3\sqrt{3}}{2} \right)=\frac{-\,3\sqrt{3}ab}{2}<0\]\[\therefore \]\[S\]is maximum, when\[\theta =\frac{2\pi }{3}\]. and maximum value of \[S=ab\left( \sin \frac{2\pi }{3}-\frac{1}{2}\cdot 2\sin \frac{2\pi }{3}\cos \frac{2\pi }{3} \right)\] \[[\because \sin 2\theta =2\sin \theta \cos \theta ]\] \[=ab\left[ \sin \left( \pi -\frac{\pi }{3} \right)-\sin \left( \pi -\frac{\pi }{3} \right)\cos \left( \pi -\frac{\pi }{3} \right) \right]\] \[=ab\left[ \sin \frac{\pi }{3}-\sin \frac{\pi }{3}\left( -\cos \frac{\pi }{3} \right) \right]\] \[=ab\left( \sin \frac{\pi }{3}+\sin \frac{\pi }{3}\cos \frac{\pi }{3} \right)=ab\left( \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\times \frac{1}{2} \right)\] \[=ab\left( \frac{2\sqrt{3}+\sqrt{3}}{4} \right)=\frac{3\sqrt{3}}{4}ab\]sq units Thus, maximum area of isosceles triangle is \[\frac{3\sqrt{3}}{4}ab\]sq units.