Application of Thermal Expansion in Solids
Category : JEE Main & Advanced
(1) Bi-metallic strip : Two strips of equal lengths but of different materials (different coefficient of linear expansion) when join together, it is called "bi-metallic strip", and can be used in thermostat to break or make electrical contact. This strip has the characteristic property of bending on heating due to unequal linear expansion of the two metal. The strip will bend with metal of greater \[\alpha \] on outer side i.e. convex side.


(2) Effect of temperature on the time period of a simple pendulum : A pendulum clock keeps proper time at temperature \[\theta \]. If temperature is increased to \[\theta '(>\theta )\] then due to linear expansion, length of pendulum and hence its time period will increase.
Fractional change in time period \[\frac{\Delta T}{T}=\frac{1}{2}\alpha \,\Delta \theta \]
(i) Due to increment in its time period, a pendulum clock becomes slow in summer and will lose time.
Loss of time in a time period \[\Delta T=\frac{1}{2}\alpha \,\,\Delta \theta \,\,T\]
(ii) Time lost by the clock in a day (t = 86400 sec)
\[\Delta t=\frac{1}{2}\alpha \,\,\Delta \theta \,\,t=\frac{1}{2}\alpha \,\,\Delta \theta \,\,(86400)=43200\,\alpha \,\,\Delta \theta \,\,sec\]
(iii) The clock will lose time i.e. will become slow if \[{\theta }'>\theta \] (in summer) and will gain time i.e. will become fast if \[{\theta }'<\theta \] (in winter).
(iv) The gain or loss in time is independent of time period T and depends on the time interval t.
(v) Since coefficient of linear expansion \[(\alpha )\] is very small for invar, hence pendulums are made of invar to show the correct time in all seasons.
(3) Thermal stress in a rigidly fixed rod : When a rod whose ends are rigidly fixed such as to prevent expansion or contraction, undergoes a change in temperature, due to thermal expansion or contraction, a compressive or tensile stress is developed in it. Due to this thermal stress the rod will exert a large force on the supports. If the change in temperature of a rod of length L is \[\Delta \theta \] then
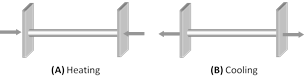
Thermal strain \[=\frac{\Delta L}{L}=\alpha \Delta \theta \] \[\left[ \text{As }\alpha =\frac{\Delta L}{L}\times \frac{1}{\Delta \theta } \right]\]
So Thermal stress \[=Y\alpha \Delta \theta \] \[\left[ \text{As }Y=\frac{\text{stress}}{\text{strain}} \right]\]
or Force on the supports \[F=YA\alpha \,\Delta \theta \]
(4) Error in scale reading due to expansion or contraction : If a scale gives correct reading at temperature \[\theta ,\] at temperature \[{\theta }'(>\theta )\] due to linear expansion of scale, the scale will expand and scale reading will be lesser than true value so that,
True value = Scale reading \[[1+\alpha \,({\theta }'-\theta )]\]
i.e. \[\text{TV}=SR\,[1+\alpha \,\Delta \theta ]\] with \[\Delta \theta =({\theta }'-\theta )\]
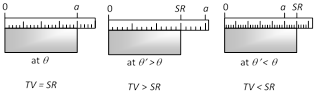
However, if \[{\theta }'<\theta \], due to contraction of scale, scale reading will be more than true value, so true value will be lesser than scale reading and will still be given by above equation with \[\Delta \theta =({\theta }'-\theta )\] negative.
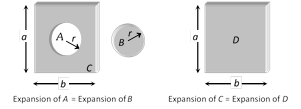
(5) Expansion of cavity : Thermal expansion of an isotropic object may be imagined as a photographic enlargement. So if there is a hole A in a plate C (or cavity A inside a body C), the area of hole (or volume of cavity) will increase when body expands on heating, just as if the hole (or cavity) were solid B of the same material. Also the expansion of area (or volume) of the body C will be independent of shape and size of hole (or cavity), i.e., will be equal to that of D.
(6) Some other application
(i) When rails are laid down on the ground, space is left between the ends of two rails.
(ii) The transmission cable are not tightly fixed to the poles.
(iii) Test tubes, beakers and crucibles are made of pyrex-glass or silica because they have very low value of coefficient of linear expansion.
(iv) The iron rim to be put on a cart wheel is always of slightly smaller diameter than that of wheel.
(v) A glass stopper jammed in the neck of a glass bottle can be taken out by warming the neck of the bottle
You need to login to perform this action.
You will be redirected in
3 sec
