Thermal Expansion in Liquids
Category : JEE Main & Advanced
(1) Liquids do not have linear and superficial expansion but these only have volume expansion.
(2) Since liquids are always to be heated along with a vessel which contains them so initially on heating the system (liquid + vessel), the level of liquid in vessel falls (as vessel expands more since it absorbs heat and liquid expands less) but later on, it starts rising due to faster expansion of the liquid.

PQ \[\to \] represents expansion of vessel
QR \[\to \] represents the real expansion of liquid
PR \[\to \] Represent the apparent expansion of liquid
(3) The actual increase in the volume of the liquid = The apparent increase in the volume of liquid + the increase in the volume of the vessel.
(4) Liquids have two coefficients of volume expansion.
(i) Co-efficient of apparent expansion \[({{\gamma }_{a}})\]: It is due to apparent (that appears to be, but is not) increase in the volume of liquid if expansion of vessel containing the liquid is not taken into account.
\[{{\gamma }_{a}}=\frac{\text{Apparent expansion in volume}}{\text{Initial volume }\times \text{ }\Delta \theta }=\frac{{{(\Delta V)}_{a}}}{V\times \Delta \theta }\]
(ii) Co-efficient of real expansion \[({{\gamma }_{r}})\] : It is due to the actual increase in volume of liquid due to heating. \[{{\gamma }_{r}}=\frac{\text{Real increase in volume}}{\text{Initial volume }\times \Delta \theta }=\frac{{{(\Delta V)}_{r}}}{V\times \Delta \theta }\]
(iii) Also coefficient of expansion of flask \[{{\gamma }_{Vessel}}=\frac{{{(\Delta V)}_{Vessel}}}{V\times \Delta \theta }\]
(iv) \[{{\gamma }_{\operatorname{Re}al}}={{\gamma }_{Apparent}}+{{\gamma }_{Vessel}}\]
(v) Change (apparent change) in volume in liquid relative to vessel is
\[\Delta {{V}_{app}}=V\,{{\gamma }_{app}}\,\Delta \theta =V({{\gamma }_{Real}}-{{\gamma }_{Vessel}})\Delta \theta =V({{\gamma }_{r}}-3\alpha )\Delta \theta \]
\[\alpha =\] Coefficient of linear expansion of the vessel. Different level of liquid in vessel
| \[\gamma \] | \[\Delta V\] | Level |
| \[{{\gamma }_{Real}}>{{\gamma }_{Vessel}}(=3\alpha )\Rightarrow {{\gamma }_{app}}>0\] | \[\Delta {{V}_{app}}\]is positive | Level of liquid in vessel will rise on heating. |
| \[{{\gamma }_{Real}}<{{\gamma }_{Vessel}}(=3\alpha )\Rightarrow {{\gamma }_{app}}<0> | \[\Delta {{V}_{app}}\] is negative | Level of liquid in vessel will fall on heating. |
| \[{{\gamma }_{Real}}={{\gamma }_{Vessel}}(=3\alpha )\Rightarrow {{\gamma }_{app}}=0\] | \[\Delta {{V}_{app}}=0\] | level of liquid in vessel will remain same. |
(5) Anomalous expansion of water : Generally matter expands on heating and contracts on cooling. In case of water, it expands on heating if its temperature is greater than \[{{4}^{o}}C\]. In the range \[{{0}^{o}}C\] to \[{{4}^{o}}C,\] water contracts on heating and expands on cooling, i.e. \[\gamma \] is negative. This behaviour of water in the range from \[{{0}^{o}}C\] to \[{{4}^{o}}C\] is called anomalous expansion.
This anomalous behaviour of water causes ice to form first at the surface of a lake in cold weather. As winter approaches, the water temperature increases initially at the surface. The water there sinks because of its increased density. Consequently, the surface reaches \[{{0}^{o}}C\] first and the lake becomes covered with ice. Aquatic life is able to survive the cold winter as the lake bottom remains unfrozen at a temperature of about \[{{4}^{o}}C\].
At \[{{4}^{o}}C,\] density of water is maximum while its specific volume is minimum.
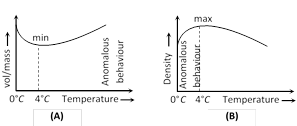
(6) Effect of temperature on upthrust : The thrust on V volume of a body in a liquid of density \[\sigma \] is given by \[Th=V\sigma g\]
Now with rise in temperature by \[\Delta {{\theta }^{o}}C,\] due to expansion, volume of the body will increase while density of liquid will decrease according to the relations \[{V}'=V(1+{{\gamma }_{S}}\Delta \theta )\] and \[{\sigma }'=\sigma /(1+{{\gamma }_{L}}\Delta \theta )\]
So the thrust \[T{h}'={V}'{\sigma }'g\]\[\Rightarrow \]\[\frac{T{h}'}{Th}=\frac{{V}'{\sigma }'g}{V\sigma g}=\frac{(1+{{\gamma }_{S}}\Delta \theta )}{(1+{{\gamma }_{L}}\Delta \theta )}\]
and apparent weight of the body \[{{W}_{app}}=\] Actual weight - Thrust
As \[{{\gamma }_{S}}<{{\gamma }_{L}}\] \[\therefore \] \[T{h}'
You need to login to perform this action.
You will be redirected in
3 sec
