| What will be the number of zeros in the square of the following number? |
| (a) 60 |
| (b) 400 |
| Factorise the following: |
| (a) \[{{x}^{2}}+9x+20\] |
| (b) \[{{p}^{2}}-13p-30~\] |
| (a) If ABCD is a square of side 14 cm and APB and DPC are semi-circles, then find the area of shaded region as shown in the figure. |
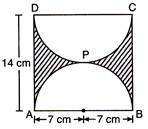 |
| (b) If area of a trapezium is 44 cm2, whose parallel sides are 10 cm and 12 cm and height is 4 cm, then verify that Area of trapezium \[=\frac{1}{2}\] [sum of parallel sides] \[\times \]height. |
| Find five rational number between. |
| (a)\[\frac{2}{3}\,\,and\,\,\frac{4}{5}~\] |
| (b)\[\frac{-3}{2}\,\,and\,\,\frac{5}{3}~\] |
| (c) \[\frac{1}{4}\,\,and\,\,\frac{1}{2}~\] |
| (a) Subtract \[4a\text{ }-\text{ }7ab\text{ }+\text{ }3b\text{ }+\text{ }12\]from |
| \[12a\text{ }-\text{ }9ab\text{ }+\text{ }5b\text{ }-\text{ }3\] |
| (b) Subtract \[3xy+\text{ }5yz-7zx\]from |
| \[5xy-\text{ }2yz-2zx+10xyz\] |
| (c) Subtract \[4{{p}^{2}}q-3pq+5p{{q}^{2}}-8p+7q-10\] |
| From \[18-3p-11q+5pq-2p{{q}^{2}}+5{{p}^{2}}q\] |
| The students of Anju's class sold posters to raise money. Anju wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise Rs. 250 for every 60 posters sold. |
| (a) How much money would Anju's class make for selling 102 posters? |
| (b) Could Anju's class raise exactly T 2,000? If so, how many posters would they need to sell? |
| (a) The sum of the digits of a two-digit number is 15. If the number formed by reversing the digits is less than the original number by 27, find the original number. |
| (b) Verify that \[x=2\]is a solution of the equation |
| \[2\left( x+1 \right)=3\left( x+1 \right)-3.\] |
| Show that: |
| (a) \[{{(3x+7)}^{2}}-84x={{(3x-7)}^{2}}\] |
| (b) \[{{\left( 9p-5q \right)}^{2}}+180\text{ }pq={{\left( 9p+5q \right)}^{2}}\] |
| (c) \[{{\left( \frac{4}{3}m-\frac{3}{4}n \right)}^{2}}+2mn=\frac{16}{9}{{m}^{2}}+\frac{9}{16}{{n}^{2}}\] |
| (d) \[\,{{(4pq+3q)}^{2}}-{{(4pq-3q)}^{2}}=48p{{q}^{2}}\] |
| Construct a pie chart for the data. | |
| A | 130 |
| B | 120 |
| C | 90 |
| D | 40 |
| E | 20 |
| Factorise the expressions and divide them as directed. |
| (a) \[\left( {{y}^{2}}+7y+10 \right)\div \left( y+5 \right)\] |
| (b) \[\left( {{m}^{2}}-14m-32 \right)\div \left( \text{m}+2 \right)\] |
| (c) \[\left( 5{{p}^{2\text{ }}}-25p+20 \right)\div \left( p-1 \right)\] |
| (d) \[4yz\left( {{z}^{2}}+\text{ }6z-16 \right)\div \text{ }2y\text{ }\left( z+8 \right)\] |
You need to login to perform this action.
You will be redirected in
3 sec
