| (a) 108 |
| (b) 616 |
| (a) \[15x{{y}^{2}},17y{{z}^{2}}\] |
| (b) \[-5{{a}^{2}}bc,11ab,13ab{{c}^{2}}\] |
(a) 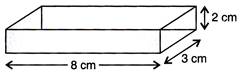 |
(b) 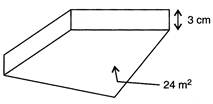 |
| (a) \[18+11x+{{x}^{2}}\] |
| (b) \[{{y}^{2}}-2y-15\] |
| (a) What will be the cost of 40 metres of the same type of cloth? |
| (b) What will be the length of the cloth bought for Rs. 810? |
| (a) height is doubled |
| (b) height is doubled and the radius is halved |
| (c) height remains same and the radius is halved. |
| Part of red pigment | 1 | 4 | 7 | 12 | 20 |
| Part of base | 8 | --- | --- | --- | --- |
| Factorise: |
| (a) \[{{a}^{4}}-{{b}^{4}}\] |
| (b) \[{{p}^{4}}-81\] |
| (c) \[{{x}^{4}}-{{(y+2)}^{4}}\] |
| (d) \[{{x}^{4}}-{{(x-z)}^{4}}\] |
| (e) \[{{a}^{4}}-2{{a}^{2}}{{b}^{2}}+{{b}^{4}}\] |
| (a) Divide 34 into two parts in such a way that \[{{\left( \frac{4}{7} \right)}^{th}}\]of one part is equal to \[{{\left( \frac{2}{5} \right)}^{th}}\]of the other. |
| (b) Which of the following equation are linear equation in one variable. |
| (a) \[{{x}^{2}}+x=1\] |
| (b) \[2x-7=\frac{2}{3}\] |
| (c) \[{{x}^{2}}+\text{ }x=10~\] |
| (d) \[x-15=3x\] |
| (a) the cost of 7 notebooks. |
| (b) the number of notebooks that can be purchased for Rs. 50. |
| (a) Find the value of the expression \[\left( 81{{x}^{2}}+16{{y}^{2}}-72xy \right),\] when \[x=\text{ }\frac{2}{3}\]and \[y=\text{ }\frac{3}{4}\] |
| (b) If a = 2 and b = 5, then verify \[{{(a+b)}^{2}}=\text{ }{{a}^{2}}+{{b}^{2\text{ }}}+2ab.\] |
| (a) Find the amount of Rs. 50000 after 2 years compounded annually. The rate of interest being 8% p.a. during the first year and 9% p.a. during the second year. Also, find the compound interest. |
| (b) If (a) decreased value \[=P{{\left( 1-\frac{R}{100} \right)}^{n}}\] and (b) depreciated value \[=P{{\left( 1+\frac{R}{100} \right)}^{n}}\] then select right answer. |
You need to login to perform this action.
You will be redirected in
3 sec
