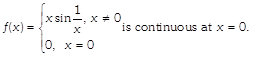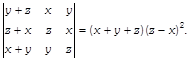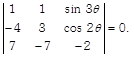-
If \[y=1-x+\frac{{{x}^{2}}}{2!}-\frac{{{x}^{3}}}{3!}+\frac{{{x}^{4}}}{4!}-....to\,\,\infty ,\] then prove that \[\frac{{{d}^{2}}y}{d{{x}^{2}}}-y=0\]
View Answer play_arrow
-
If A and B are matrices of order 3 and \[|A|\,\,=5,\] \[|B|\,\,=3,\] find \[|3AB|.\]
View Answer play_arrow
-
Find the direction cosines of the line passing through the two points \[(-\,2,\,\,4,\,\,-\,5)\] and (1, 2, 3).
View Answer play_arrow
-
Evaluate \[\int_{0}^{1}{{{3}^{x-\,|x|}}dx.}\]
View Answer play_arrow
-
If \[\vec{a}\] and \[\vec{b}\] are the position vectors of A and B respectively, find the position vector of a point C on BA produced such that BC = 1.5 BA
View Answer play_arrow
-
Show that the function f(x} given by
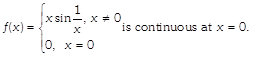
-
Prove that the function given by \[f(x)={{x}^{3}}-3{{x}^{2}}+3x-100\] is increasing in R.
View Answer play_arrow
-
Evaluate \[\int{\frac{1}{\sqrt{1+\sin 2x}}}\,\,dx.\]
View Answer play_arrow
-
Differentiate log sin x with respect to \[\sqrt{\cos x}.\]
View Answer play_arrow
-
If the radius of a circle is increased from 5 cm to 5.1 cm. Find the approximate increase in area.
View Answer play_arrow
-
A fair die is rolled. Consider the following events A = {2, 4, 6}, B= {4, 5} and C={3, 4, 5, 6}.Find (i) \[P(A\cup B/C)\] (ii) \[P(A\cap B/C).\]
View Answer play_arrow
-
Show that the determinant value of a skew-symmetric matrix of odd order is always zero.
View Answer play_arrow
-
Solve the following differential equation: \[{{(x\,+y)}^{2}}\frac{dy}{dx}={{a}^{2}}\]
View Answer play_arrow
-
| Find the minimum value of n for which |
| \[{{\tan }^{-1}}\frac{n}{\pi }>\frac{\pi }{4},\] \[n\in N.\] |
| OR |
| Show that \[\tan \left( \frac{1}{2}{{\sin }^{-1}}\frac{3}{4} \right)=\frac{4-\sqrt{7}}{3}.\] |
View Answer play_arrow
-
Find the equation of a curve passing through the point (0, 1), if the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x-coordinate (abscissa) and the product of the x-coordinate and y-coordinate (ordinate) of that point.
View Answer play_arrow
-
| Evaluate \[\int{\frac{1+{{x}^{2}}}{1+{{x}^{4}}}\,dx.}\] |
| OR |
| Evaluate \[\int{x\cdot {{(\log \,\,x)}^{2}}\,dx.}\] |
View Answer play_arrow
-
| Using the properties of determinants, show that |
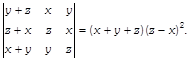 |
| OR |
| Find the value of \[\theta \] satisfying |
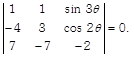 |
View Answer play_arrow
-
Using properties of definite integrals, evaluate \[\int_{\pi /6}^{\pi /3}{\frac{dx}{1+\sqrt{\tan \,\,x}}.}\]
View Answer play_arrow
-
In an activity organised in the school, Rohan was given the task to put the slogan 'Satyamev Jayte' on a trapezium shaped card sheet. If the length of three sides of a trapezium other than base are equal to 10 cm, find the area of the trapezium when it is maximum. Explain the meaning of 'Satyamev Jayte'.
View Answer play_arrow
-
Find the coordinates of the point, where the line passes through the points A (3, 4, 1) and "B (5, 1, 6) crosses the XY-plane.
View Answer play_arrow
-
A can hit target 4 times out of 5 times, B can hit target 3 times out of 4 times and C can hit target 2 times out of 3 times. They fire simultaneously. Find the probability that (i) Any two out of A, B and C will hit the target. (ii) None of them will hit the target.
View Answer play_arrow
-
Let \[\vec{a}=2\hat{i}+\hat{k},\] \[\vec{b}=\hat{i}+\hat{j}+\hat{k}\] and \[\vec{c}=4\hat{i}-3\hat{j}+7\hat{k}\] be three vectors. Fine a vector \[\vec{r}\] which satisfies \[\vec{r}\times \vec{b}=\vec{c}\times \vec{b}\] and \[x+y=v\]
View Answer play_arrow
-
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1/4 be the probability that he guesses. Assuming that, a student who guesses at the answer will be correct with probability 1/4. What is the probability that a student knows the answer given that he answered it correctly?
View Answer play_arrow
-
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is almost half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by almost 600 units. If the company makes profit of Rs. 12 and Rs. 16 per doll respectively on dolls A and B, then how many of each should be produced weekly in order to maximize the profit? Why are small scale industries important in India? What values are being promoted by establishing small scale industries?
View Answer play_arrow
-
Show that the normal at any point \[\theta \] to the curve \[x=a\cos \theta +a\,\theta \sin \theta \] and \[y=asin\theta -a\,\theta \cos \theta \] is at a constant distance from the origin.
View Answer play_arrow
-
| Find the image of the point (1, 6, 3) on the line \[\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}.\] |
| Also, write the equation of the line joining the given point and its image and find the length of segment joining the given point and its image. |
| OR |
| Find the foot of the perpendicular from the point (0, 2, 3) on the line \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}.\] |
| Also, find the length of the perpendicular. |
View Answer play_arrow
-
Find the area of the smaller region bounded by the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] and the line \[\frac{x}{a}+\frac{y}{b}=1.\]
View Answer play_arrow
-
| The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By addinq first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method. |
| OR |
| Solve the following system of equations by matrix method, where \[x\ne 0,\] \[y\ne 0\] and \[z\ne 0.\] |
| \[\frac{2}{x}-\frac{3}{y}+\frac{3}{z}=10,\] \[\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=10\] |
| and \[\frac{3}{x}-\frac{1}{y}+\frac{2}{z}=13\] |
View Answer play_arrow
-
| Let \[A=\{x\in R:0\le x\le 1\}.\] If \[f:A\to A\] is defined by |
| \[f(x)=\left\{ \begin{matrix} x, & i\text{f}\,\,x\in Q \\ 1-x & \text{if}\,\,x\notin Q \\ \end{matrix} \right.\] |
| Then prove that \[fof(x)=x\] for all \[x\in A.\] |
| OR |
| Let \[A=N\times N\] and * be the binary operation on A defined by (a, b) * (c, d) = \[(a+c,\,\,b+d)\] |
| Show that * is commutative and associative. |
| Find the identity element for * on A, if any. |
View Answer play_arrow