question_answer

In an activity organised in the school, Rohan was given the task to put the slogan 'Satyamev Jayte' on a trapezium shaped card sheet. If the length of three sides of a trapezium other than base are equal to 10 cm, find the area of the trapezium when it is maximum. Explain the meaning of 'Satyamev Jayte'.

Answer:

Let ABCD be a trapezium such that DC is parallel to AB and AD = 10cm = DC = BC.               Now, draw perpendiculars DP and CQ from D and C, on AB, respectively. \[\therefore \]      \[\Delta APD\sim \Delta BQC\]                         Therefore,     PA = QB = x cm 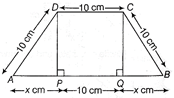                 In right angled \[\Delta APD,\] we have       \[A{{D}^{2}}=A{{P}^{2}}+P{{D}^{2}}\]            [by Pythagoras theorem] \[\Rightarrow \]   \[P{{D}^{2}}=A{{D}^{2}}-A{{P}^{2}}\] \[\Rightarrow \]   \[PD=\sqrt{A{{D}^{2}}-A{{P}^{2}}}\] \[\Rightarrow \]   \[PD=\sqrt{100-{{x}^{2}}}cm\] Similarly, in \[\Delta BQC,\,\,QC=\sqrt{100-{{x}^{2}}}cm\] If A denotes the area of the trapezium ABCD, then \[A=f(x)=\frac{1}{2}\](Sum of parallel sides) \[\times \] Height \[\Rightarrow \]   \[f(x)=\frac{1}{2}(AB+DC)\times PD\] \[\Rightarrow \]   \[f(x)=\frac{1}{2}[(2x+10)\times 10]\times \sqrt{100-{{x}^{2}}}\] \[\Rightarrow \]   \[f(x)=(x+10)\sqrt{100-{{x}^{2}}}\]                      ?(i) On differentiating both sides of Eq. (i) w.r.t. x, we get \[f'(x)=1\sqrt{100-{{x}^{2}}}+(x+10)\left( \frac{-\,2x}{2\sqrt{100-{{x}^{2}}}} \right)\] \[\Rightarrow \] \[f'(x)=\frac{(100-{{x}^{2}})-{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\] \[=\frac{100-2{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\] Again differentiating both sides w.r.t. x, we get \[f'(x)=\frac{\left[ \begin{align}   & \sqrt{100-{{x}^{2}}}(-\,4x-10) \\  & -(100-2{{x}^{2}}-10x)\left( \frac{-\,2x}{2\sqrt{100-{{x}^{2}}}} \right) \\ \end{align} \right]}{(100-{{x}^{2}})}\] \[=\frac{\left[ (100-{{x}^{2}})(-\,4x-10)+(100x-2{{x}^{3}}-10{{x}^{2}}) \right]}{(100-{{x}^{2}})\sqrt{100-{{x}^{2}}}}\] \[=\frac{\left[ (-\,400x-1000+4{{x}^{3}}+10{{x}^{2}})+(100x-2{{x}^{3}}-10{{x}^{2}}) \right]}{(100-{{x}^{2}})\sqrt{100-{{x}^{2}}}}\] For maxima or minima, put             \[f'(x)=0\] \[\Rightarrow \]   \[\frac{100-2{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}=0\] \[\Rightarrow \]   \[100-2{{x}^{2}}-10x=0\] \[\Rightarrow \]   \[2{{x}^{2}}+10x-100=0\] \[\Rightarrow \]   \[2({{x}^{2}}+5x-50)=0\] \[\Rightarrow \]   \[{{x}^{2}}+5x-50=0\] \[\Rightarrow \]   \[{{x}^{2}}+10x-5x-50=0\] \[\Rightarrow \]   \[x(x+10)-5(x+10)=0\] \[\Rightarrow \]   \[(x+10)(x-5)=0\] \[\therefore \]      \[x=-\,10,\] x = 5 \[\Rightarrow \]x = 5 [\[\because \,\,x\] represents distance, so it cannot be negative] On putting x = 5 in Eq. (ii), we get \[{{[f''(x)]}_{at\,\,x=5}}=\frac{\left( \begin{align}   & [-\,400(5)-1000+4{{(5)}^{3}}+10{{(5)}^{2}} \\  & +[100(5)-2{{(5)}^{3}}-10{{(5)}^{2}}] \\ \end{align} \right)}{(100-25)\sqrt{100-25}}\] \[=\frac{(-\,3000+500+250)+(500-250-250)}{75\sqrt{75}}\] \[=\frac{-\,2250}{75\sqrt{75}}=\frac{-\,30}{\sqrt{75}}<0\] Hence, the area of trapezium is maximum, when x = 5 and the area is given by \[f(5)=(5+10)\sqrt{100-25}=15\sqrt{75}=75\sqrt{3}\,c{{m}^{2}}\] Value 'Satyamev Jayte' means truth always wins. We should always follow the path of truth in our life.