question_answer

The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By addinq first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.

OR

Solve the following system of equations by matrix method, where \[x\ne 0,\] \[y\ne 0\] and \[z\ne 0.\]

\[\frac{2}{x}-\frac{3}{y}+\frac{3}{z}=10,\] \[\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=10\]

and       \[\frac{3}{x}-\frac{1}{y}+\frac{2}{z}=13\]

Answer:

Let first, second and third numbers be denoted by x,  y and z, respectively.

Then, according to the question,

\[x+y+z=6,\text{ }y+3z=11\]

and       \[x+z=2y\]

\[\Rightarrow \]   \[x-2y+z=0\]

In matrix form, this system of equations can be written as

AX = B                                        ...(i)

Where 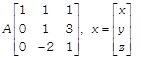  and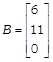

Here,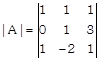

\[=1(1+6)-1(0-3)+1(0-1)\]

[expanding along \[{{R}_{1}}\]]

\[=7+3-1=9\ne 0\]

Since, \[|A|\,\ne 0,\] so the inverse of A exists.

Now, cofactors corresponding to each element of |A| are

\[{{C}_{11}}={{(-\,1)}^{1+1}}\left| \begin{matrix}    1 & 3  \\    -\,2 & 1  \\ \end{matrix} \right|=1+6=7\]

\[{{C}_{12}}={{(-\,1)}^{1+2}}\left| \begin{matrix}    0 & 3  \\    1 & 1  \\ \end{matrix} \right|=-(0-3)=3\]

\[{{C}_{13}}={{(-\,1)}^{1+3}}\left| \begin{matrix}    0 & 1  \\    1 & -\,2  \\ \end{matrix} \right|=0-1=-\,1\]

\[{{C}_{21}}={{(-\,1)}^{2+1}}\left| \begin{matrix}    1 & 1  \\    -\,2 & 1  \\ \end{matrix} \right|=-(1+2)=-\,3\]

\[{{C}_{22}}={{(-\,1)}^{2+2}}\left| \begin{matrix}    1 & 1  \\    1 & 1  \\ \end{matrix} \right|=0\]

\[{{C}_{23}}={{(-\,1)}^{2+3}}\left| \begin{matrix}    1 & 1  \\    1 & -\,2  \\ \end{matrix} \right|=-(-\,2-1)=3\]

\[{{C}_{31}}={{(-\,1)}^{3+1}}\left| \begin{matrix}    1 & 1  \\    1 & 3  \\ \end{matrix} \right|=3-1=2\]

\[{{C}_{32}}={{(-\,1)}^{3+2}}\left| \begin{matrix}    1 & 1  \\    0 & 3  \\ \end{matrix} \right|=-(3-0)=-\,3\]

\[{{C}_{33}}={{(-\,1)}^{3+3}}\left| \begin{matrix}    1 & 1  \\    0 & 1  \\ \end{matrix} \right|=1-0=1\]

Then, adj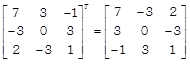

Thus,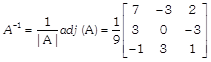

Now, the solution of Eq. (i) is given by

\[X={{A}^{-1}}B\]                                ?(ii)

On putting the values of \[{{A}^{-1}}\] and B in RHS of Eq. (ii) we get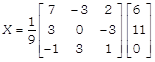

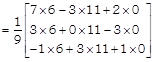
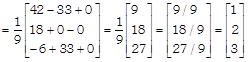
\[\Rightarrow \]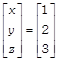

On comparing both sides, we get

x = 1, y = 2 and z = 3

Which are the required numbers.

OR

Given system of equations can be written in matrix form as AX = B                         ?(i)

Where 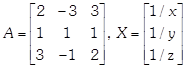and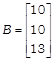

Now,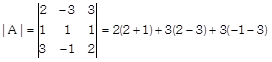

\[=6-3-12=-\,9\ne 0\]

\[\therefore \,\,{{A}^{-1}}\text{exists}.\]

Now, cofactors of elements of |A| are

\[{{C}_{11}}={{(-\,1)}^{1+1}}\left| \begin{matrix}    1 & 1  \\    -\,1 & 2  \\ \end{matrix} \right|=2+1=3\]

\[{{C}_{12}}={{(-\,1)}^{1+2}}\left| \begin{matrix}    1 & 1  \\    3 & 2  \\ \end{matrix} \right|=-(2-3)=1\]

\[{{C}_{13}}={{(-\,1)}^{1+3}}\left| \begin{matrix}    1 & 1  \\    3 & -\,1  \\ \end{matrix} \right|=-\,1-3=-\,4\]

\[{{C}_{21}}={{(-\,1)}^{2+1}}\left| \begin{matrix}    -\,3 & 3  \\    -\,1 & 2  \\ \end{matrix} \right|=-\,(-\,6+3)=3\]

\[{{C}_{22}}={{(-\,1)}^{2+2}}\left| \begin{matrix}    2 & 3  \\    3 & 2  \\ \end{matrix} \right|=4-9=-\,5\]

\[{{C}_{23}}={{(-\,1)}^{2+3}}\left| \begin{matrix}    2 & -\,3  \\    3 & -\,1  \\ \end{matrix} \right|=-(-\,2+9)=-\,7\]

\[{{C}_{31}}={{(-\,1)}^{3+1}}\left| \begin{matrix}    -\,3 & 3  \\    1 & 1  \\ \end{matrix} \right|=-\,3-3=-\,6\]

\[{{C}_{32}}={{(-\,1)}^{3+2}}\left| \begin{matrix}    2 & 3  \\    1 & 1  \\ \end{matrix} \right|=-(2-3)=1\]

\[{{C}_{33}}={{(-\,1)}^{3+3}}\left| \begin{matrix}    2 & -\,3  \\    1 & 1  \\ \end{matrix} \right|=2+3=5\]

\[\therefore \] adj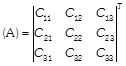

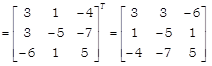
\[\because \] \[{{A}^{-1}}=\frac{1}{|A|}\] adj(A)

\[\Rightarrow \]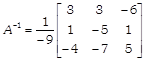

Now, Eq. (i) can be written as \[X={{A}^{-1}}B.\]

i.e.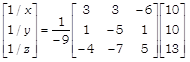

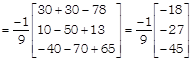
[dividing each element by \[-\,9\]]

\[\therefore \]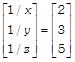

On comparing the corresponding elements, we get

\[\frac{1}{x}=2\] \[\Rightarrow \] \[x=\frac{1}{2}\]

\[\frac{1}{y}=3\] \[\Rightarrow \] \[y=\frac{1}{3}\]

and       \[\frac{1}{z}=5\] \[\Rightarrow \] \[z=\frac{1}{5}\]

Hence, \[x=\frac{1}{2},\] \[y=\frac{1}{3}\]

and       \[z=\frac{1}{5}\]