question_answer

Using the properties of determinants, show that

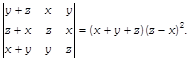OR

Find the value of \[\theta \] satisfying

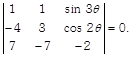Answer:

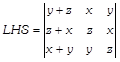
Applying \[{{R}_{1}}\to {{R}_{1}}+{{R}_{2}}+{{R}_{3}},\] we get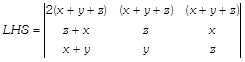

On taking common \[(x+y+z)\] from \[{{R}_{1}},\] we get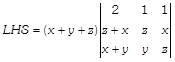

Applying \[{{C}_{1}}\to {{C}_{1}}-2{{C}_{3}}\] and \[{{C}_{2}}\to {{C}_{2}}-{{C}_{3}},\] we get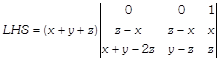

Expanding along \[{{R}_{1}},\] we get

\[LHS=(x+y+z)[(z-x)(y-z)-(x+y-2z)(z-x)]\]\[=(x+y+z)[(z-x)(y-z-x-y+2z)]\]

\[=(x+y+z)[(z-x)(z-x)]\]

\[=(x+y+z){{(z-x)}^{2}}\]

= RHS                                    Hence proved.

OR

Given,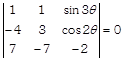

\[\Rightarrow \]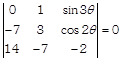

[applying \[{{C}_{1}}\to {{C}_{1}}-{{C}_{2}}\]]

\[\Rightarrow \]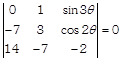

[taking 7 common from \[{{C}_{1}}\]]

\[\Rightarrow \]   \[7[0-1(2-2cos2\theta )+sin3\theta (7-6)]=0\]

[expanding along \[{{R}_{1}}\]]

\[\Rightarrow \]   \[-\,14+14\cos 2\theta +7\sin 3\theta =0\]

\[\Rightarrow \]   \[14\cos 2\theta +7\sin 3\theta =14\]

\[\Rightarrow \]   \[14(1-2si{{n}^{2}}\theta )+7(3\sin \theta -4{{\sin }^{3}}\theta )=14\]

\[\left[ \begin{align}   & \because \,\,\cos 2\theta =1-2{{\sin }^{2}}\theta \,\,and \\  & \sin 3\theta =3\sin \theta -4{{\sin }^{3}}\theta  \\ \end{align} \right]\]

\[\Rightarrow \]   \[14-28si{{n}^{2}}\theta +21\sin \theta -28{{\sin }^{3}}\theta =14\]

\[\Rightarrow \]   \[-\,28si{{n}^{2}}\theta -28{{\sin }^{3}}\theta +21\sin \theta =0\]

\[\Rightarrow \]   \[4si{{n}^{3}}\theta +4{{\sin }^{2}}\theta -3\sin \theta =0\]

[dividing by \[(-\,7)\]]

\[\Rightarrow \]   \[sin\theta (4{{\sin }^{2}}\theta +4\sin \theta -3)=0\]

Then, \[sin\theta =0\] \[\Rightarrow \] \[\theta =n\,\pi \]

or         \[4si{{n}^{2}}\theta +4\sin \theta -3=0\]

Which is a quadratic equation in \[\sin \theta .\]

\[\therefore \]      \[\sin \theta =\frac{-4\pm \sqrt{16+48}}{8}=\frac{-\,4\pm \sqrt{64}}{8}\]

\[=\frac{-4\pm 8}{8}=\frac{4}{8},\] \[\frac{-\,12}{8}\]\[\Rightarrow \] \[\sin \theta =\frac{1}{2},\,\,\frac{-\,3}{2}\]

Here, \[\sin \theta \ne \frac{-\,3}{2}\] [not possible, because \[-1\le \sin \theta \le 1\]]

\[\therefore \]      \[\sin \theta =\frac{1}{2}=\sin \frac{\pi }{6},\] then

\[\theta =n\,\pi \,+{{(-\,1)}^{n}}\frac{\pi }{6}\]

Hence, the required values of \[\theta \] are \[n\,\pi \,+{{(-\,1)}^{n}}\frac{\pi }{6}\] and \[n\,\pi .\]