Quadrilaterals
Category : 9th Class
Quadrilaterals
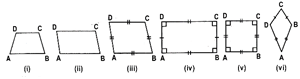
(i) Trapezium:
(a) A quadrilateral having exactly one pair of parallel sides is called a trapezium.
(b) A trapezium is said to be an isosceles trapezium if its non-parallel sides are equal.
ABCD is a trapezium in which AB || DC.
This trapezium is said to be an isosceles trapezium if AB || DC and AD = BC.
(ii) Parallelogram: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
ABCD is a parallelogram in which AB || DC and AD II BC.
Properties:
(a) In a parallelogram, any two opposite sides are equal.
(b) In a parallelogram, any two opposite angles are equal.
(c)In a parallelogram, the diagonals bisect each other.
(d) In a parallelogram, each diagonal divides it into two congruent triangles.
(e) In a parallelogram, any two adjacent angles have their sum equal to \[{{180}^{o}}\] i.e. the adjacent angles are supplementary.
(iii) Rhombus: A quadrilateral having all sides equal is called a rhombus.
ABCD is a rhombus in which AB II DC, AD || BC and AB = BC = CD = DA.
Properties:
(a) The diagonals of a rhombus bisect each other at right angles.
(b) Each diagonal of a rhombus divides it into two congruent triangles.
(c) Opposite angles of a rhombus are equal and the sum of any two adjacent angles is\[{{180}^{o}}\]
(d) The opposite sides of a rhombus are parallel.
(e) All the sides of a rhombus are equal.
(iv) Rectangle: A parallelogram whose angles are all right angles is called a rectangle.
ABCD is a rectangle in which,
AD || BC and AB || CD and
\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]
(a) Opposite sides of a rectangle are equal and opposite angles of a rectangle are equal.
(b) The diagonals of a rectangle bisect each other.
(c) Each diagonal divides the rectangle into two congruent triangles.
(d) The diagonals of a rectangle are equal.
(v) Square: A parallelogram having all sides equal and each angle equal to a right angle is called a square.
ABCD is a square in which AB || DC, AD || BC,
AB = BC = CD = DA and ZA = ZB = ZC = ZD= 90°.
(a) All sides are equal.
(b) All angles are equal.
(c) The diagonals are equal and bisect each other at right angles.
(d) Each diagonal divides the square into two congruent right angled isosceles triangles.
(vi) Kite: A quadrilateral having two pairs of equal adjacent sides but unequal opposite sides is called a kite.
ABCD is a kite in which AB = AD and BC = CD.
(a) Both pairs of opposite sides should be equal (or)
(b) One pair of opposite sides should be equal and parallel (or)
(c) Both pairs of opposite angles should be equal (or)
(d) Its diagonals should bisect each other.
(a) All its angles should be right angles (or)
(b) Its diagonals should be equal and bisect each other (or)
(c) Both pairs of opposite sides should be equal and one angle must be 90° (or)
(d) Both pairs of opposite sides and its diagonals should be equal.
Conditions for a quadrilateral to become a rhombus:
(a) All its sides should be equal (or)
(b) Its diagonals should bisect each other at right angles (or)
(c) Both pairs of its opposite sides should be equal and the diagonals should intersect at right angles.
(a) All its sides should be equal and one angle must be 90° (or)
(b) All its sides and the diagonals should be equal (or)
(c) All its angles should be equal and the diagonals should intersect at right angles.
(i) To construct a quadrilateral, 5 independent measurements are needed.
(ii) To construct a trapezium, 4 independent measurements are required.
(iii) To construct a parallelogram, 3 independent measurements are required.
(iv) To construct a rhombus, 2 independent measurements are required.
(v) To construct a rectangle, 2 independent measurements are required.
(vi) To construct a square, 1 measurement is required.
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and half of it.
You need to login to perform this action.
You will be redirected in
3 sec
