9th Class Mathematics Quadrilaterals Quadrilateral

 QUADRILATERAL

FUNDAMENTALS

• Quadrilateral is a figure which is bounded by four straight lines. A quadrilateral has four vertices, four sides, four angles and sum of angles is\[{{360}^{{}^\circ }}\].

TYPES OF QUADRILATERAL

• Square:-

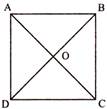
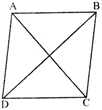
A quadrilateral which sides are equal and each angle is equal to \[{{90}^{{}^\circ }}\] is called square.

Diagonals of square are equal and cut each other at\[{{90}^{{}^\circ }}\].

i.e., \[AB=BC=CD=DA\].

\[\angle A=\angle B=\angle C=\angle D\]

and \[AC=CD\].

• Rectangle

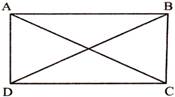
A quadrilateral whose all angles arc right angle and. each pair of opposite sides are equal is called Rectangle.

i.e., \[\angle A=\angle \mathbf{B}=\angle C=\angle D={{90}^{{}^\circ }}\], and \[AB=CD,AD=BC\] The diagonals of rectangle are equal and bisect each other at right angle. Each diagonal divides rectangle into congruent triangles.

i.e., \[AC=BD\] and \[\Delta ADC=\Delta ABC\], \[\Delta ABD=\Delta BCD\]

• Trapezium: A, quadrilateral in which exactly one pair of parallel sides are equal is called a trapezium

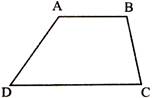
\[AB\parallel CD\]

• A trapezium, is an isosceles trapezium if its non - parallel sides are equal.
• ABCD is a isosceles trapezium if

            \[AB\parallel CD\text{ }and\text{ }AD=BC\].

• Parallelogram:- A quadrilateral having both pairs of opposite sides are equal is called a. parallelogram,

• In parallelogram ABCD \[AB\parallel CD\] and \[AD=BC\],
• In a parallelogram two opposite sides are equal.

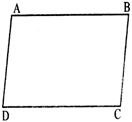
i.e., \[AD=BC,AB=CD\]

• In a. parallelogram two opposite angles are equal

i.e., \[\angle A=\angle C\] and \[\angle B=\angle D\].

• In a parallelogram sum of two adjacent angles is \[{{180}^{{}^\circ }}\]e., \[\angle A+\angle B={{180}^{{}^\circ }},\angle B+\angle C={{180}^{{}^\circ }}\]

\[\angle C+\angle D={{180}^{{}^\circ }}\]and \[\angle D+\angle A={{180}^{{}^\circ }}\]

• Each diagonal of a parallelogram divides it into two congruent triangles.

            i.e., \[\Delta ABC=\Delta ADC\]

            \[\Delta ABD=\Delta BCD\]

• Rhombus:- A quadrilateral which all sides are equal is called a rhombus.

• The opposite side of a rhombus are parallel.

i.e., \[AB\parallel CD\]and \[BC\parallel 2AD\]

• Opposite angles of a rhombus are equal

i.e., \[\angle A=\angle C\] and \[\angle B=\angle D\]

• Each diagonal of a rhombus divides it into two congruent triangles.