9th Class Mathematics Quadrilaterals Quadrilateral

       Introduction

We know that a plane figure which is bounded by four line segments is called quadrilateral. Previously we have studied about different types of quadrilateral like rectangle, square, parallelogram etc. In this chapter, we will discuss about different properties of quadrilateral with the help of theorems.  

        Quadrilateral In the figure given below:

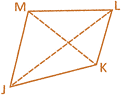
(i) Points J, K, L and M are the vertices of quadrilateral JKLM.

(ii) The line segments J, K, L, LM and JM are the sides of this quadrilateral.

(iii) The two sides of a quadrilateral having a common point is called adjacent side.

(iv) The two sides have no common end point is called opposite side.

(v) Two angles of a quadrilateral having common arm is called adjacent angle.

(vi) Two angles of a quadrilateral having no common arm is called vertically opposite angles.  

            Theorem on a Quadrilateral  

Theorem 1: The sum of all interior angles of a quadrilateral is 360°  

Given: A quadrilateral PQSR  

To Prove:

\[\angle \text{P}+\angle \text{Q}+\angle \text{R}+\angle \text{S}=\text{36}0{}^\circ \]  

Construction:

Join PQ

Proof:

In \[\Delta \text{PQR}\]

\[\angle \text{Q}+\angle \text{QPR}+\angle \text{QRP}=\text{18}0{}^\circ \]                  .....(i)

In \[\Delta \text{PRS}\] \[\angle \text{S}+\angle \text{SRP}+\angle \text{SPR}=\text{18}0{}^\circ \]                     .....(ii)

Adding (i) and (ii), we get:

\[\angle \text{Q}+\angle \text{S}+(\angle \text{QPR}+\angle \text{SPR})+(\angle \text{QRP}+\angle \text{SRP})=\text{36}0{}^\circ \]

\[\Rightarrow \] \[\angle \text{Q}+\angle \text{S}+\angle \text{P}+\angle \text{R}=\text{36}0{}^\circ \]

[Because \[\angle \text{QPR}+\angle \text{SPR}=\angle \text{P},\angle \text{QRP}+\angle \text{SRP}=\angle \text{R}\]]

Hence, proved  

Theorem 2:

In a parallelogram opposite sides and opposite angles are equal and diagonals bisect each other.  

Given:

A parallelogram PQSR, PQ II RS and PS II QR  

To Prove:

(i) \[\text{PQ}=\text{RS},~~~~\text{PS}=\text{QR}\]

(ii) \[\angle \text{P}=\angle \text{R}\] and \[\angle \text{Q}=\angle \text{S}\]

(iii) 0 is the midpoint of PR and SQ

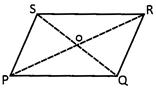
Proof:

In\[\Delta \text{PQR}\]and\[\Delta \text{RSP}\]

\[\angle \text{RPQ}=\angle \text{PRS},\]             (Alternate)

\[\angle \text{PRQ}=\angle \text{RPS}\]

and \[PR=PR\]                   (Common)

\[\Delta \text{PQR}=\Delta \text{PRS}\]

By C.P.C.T. (Corresponding part of congruence triangle PQ = RS, and PS = QR and\[\angle \text{Q}=\angle \text{S}\].

Similarly In

\[\Delta \text{PQS}\] and \[\Delta \text{QSR}\]

we get:

\[\Delta P\text{QS}\cong \Delta QSS\]                  

\[\Rightarrow \]              \[\angle P=\angle R\]

so,  

\[PQ=RS\] and \[PS=QR\]         Proved

\[\angle P=\angle R\] and \[\angle Q=\angle S\]       Proved              

Now In

\[\Delta \text{POQ}\] and \[\Delta \text{ROS}\]

\[\angle \text{OPQ}=\angle \text{ORS}\]             (Alternate)        

\[\angle \text{OQP}=\angle \text{OSR}\]

And        \[\text{PQ}=\text{QR}\]                                           (Opposite of Parallelogram)

\[\Rightarrow \]   \[\Delta POQ\cong \Delta SOR\]                           (By ASA)

\[\Rightarrow \]    PO = OR and QO = OS                (By CPCT)

\[\Rightarrow \] O is the midpoint of PR and QS                                                     (Hence, proved)