10th Class Mathematics Introduction to Trigonometry Trigonometry

TRIGONOMETRY

Systems of Measurement of an Angle

Circular System

In this system, the angle is measured in radians.

Radian: The angle subtended by an arc length APB equal to the radius of a circle at its centre is defined of one radian (see figure). It is written as \[{{1}^{c}}\]. (‘c’ denotes radian)

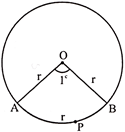
Relation between the Units

Look at the circle in the above figure and note that,

\[360{}^\circ =2{{\pi }^{c}}\Rightarrow 90{}^\circ =\frac{{{\pi }^{c}}}{2}\] and \[45{}^\circ =\frac{{{\pi }^{c}}}{4}\]; Or, simply, \[90{}^\circ =\frac{\pi }{2},45{}^\circ =\frac{\pi }{4}\]

For convenience, the above relation can be written as, \[\frac{D}{90}=\frac{R}{\frac{\pi }{2}}\], where, D denotes degrees, and R radians.

Remember

1. \[1{}^\circ =\frac{\pi }{180}\] radian \[=0.0175\] radians (approximately).
2. \[1{}^\circ =\frac{180}{\pi }\] degrees \[=57{}^\circ 17'44''\] (approximately).
3. \[30{}^\circ =\frac{\pi }{6},45{}^\circ =\frac{\pi }{4};60{}^\circ =\frac{\pi }{3};90{}^\circ =\frac{\pi }{2};120{}^\circ =\frac{2\pi }{3},180{}^\circ =\pi \]

Note: If no unit of measurement is shown for any angle, it is considered as radian.

Trigonometric Ratios

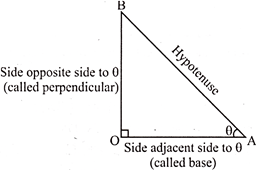
Let AOB be a right triangle with \[\angle AOB\] as \[90{}^\circ \]. Let \[\angle OAB\]be \[\theta \]. Notice that \[0{}^\circ <9<90{}^\circ \]. That is, \[\theta \] is an acute angle (see adjacent figure).

Six possible ratios among the three sides of the triangle AOB, are possible. They are called trigonometric ratios.

1. Sine of the angle \[\theta \] or, simply \[\text{sin}\theta \]: \[\sin \theta =\frac{Perpendicular}{Hypotenuse}=\frac{p}{h}=\frac{OB}{AB}\]
2. Cosine of the angle \[\theta \] or, simply \[\cos \theta \]: \[\cos \theta =\frac{Base}{Hypotenuse}=\frac{b}{h}=\frac{OA}{AB}\].
3. Tangent of the angle \[\theta \] or, simply \[tan\theta \]: \[\tan \theta =\frac{perpendicular}{base}=\frac{p}{b}=\frac{OB}{OA}\]
4. Cotangent of the angle \[\theta \] or, simply \[\cot \,\theta \]: \[\cot \theta =\frac{base}{perpendicular}=\frac{b}{p}=\frac{OA}{OB}\]
5. Cosecant of the angle \[\theta \] or, simply \[cosec\theta \]: \[co\sec \,\,\theta =\frac{hypetenuse}{perpendicular}=\frac{h}{p}=\frac{AB}{OB}\]
6. Secant of the angle \[\theta \] or, simply \[sec\theta \]: \[\sec \,\,\theta =\frac{h}{b}=\frac{AB}{OB}\]

We observe that,

1. \[\cos ec\,\theta =\frac{1}{\sin \,\theta },\sec \,\theta =\frac{1}{\cos \,\theta }\] and \[\cot \,\theta =\frac{1}{\tan \,\theta }\];
2. Also, \[\tan \,\theta =\frac{\sin \,\theta }{\cos \,\theta }=\left( \frac{p/h}{b/h} \right)\] and \[co\operatorname{t}\,\theta =\frac{\cos \,\theta }{\sin \,\theta }=\left( \frac{b/h}{p/h} \right)\]

PYTHAGOREAN TRIPLETS

Pythagorean Triplets are basically sides of a right A which obey Pythagoras theorem.

Examples are:

1. 3, 4, 5 (and all their multiples in the form of 3k, 4k, 5k etc. for eg. 6, 8, 19 & etc.)
2. 8, 15, 17 (and all their multiples in the form of 8k, 15k, 17k etc.)
3. 9, 49, 41 (and all their multiples in the form of 9k, 49k, 41k etc.)
4. 1, 2. 4, 2.6 (and all their multiples in the form of 1k, 2.4k, 2.6k etc.)
5. 5, 12, 13 (and all their multiples in the form of 5k, 12k, 13k etc.)
6. 7, 24, 25 (and all their multiples in the form of 7k, 24k, 25k etc.)

Example: If \[\cos \theta =\frac{2}{5}\], then find the values of \[\tan \,\theta ,\cos ec\,\theta .\]

Solution:

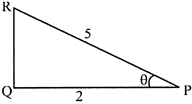
Given, \[\cos .\theta =\frac{2}{5}\]

Let PQR be the right triangle such that \[\angle QPR=\theta \] (see figure)

Assume that \[PQ=2\] and \[PR=5\].

Then, \[QR=\sqrt{P{{R}^{2}}-P{{Q}^{2}}}=\sqrt{25-4}=\sqrt{21}\]

So, \[\tan \,\theta =\frac{Opposite\,\,side\,\,to\,\,\angle \theta }{base}=\frac{QR}{PQ}=\frac{\sqrt{21}}{2}\]  and \[\cos ec\,\theta =\frac{Hypotenuse}{perpendicular}=\frac{PR}{QR}=\frac{5}{\sqrt{21}}\]

Trigonometric Identities

1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[cose{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
4. \[\sin (90-\theta )=cos\theta ;\,\,\,\,cos(90-\theta )=sin\theta \]
5. \[\sec (90-\theta )=cosec\theta ;\,\,\,\,cosec(90-\theta )=\sec \theta \]
6. \[ten(90-\theta )=cot\theta ;\,\,\,\,cot(90-\theta )=ten\theta \]

Value of Trigonometric Ratios for Specific Angles

Note:

1. For \[\theta =\frac{\pi }{4}\] (or \[45{}^\circ \]) \[sin\theta =cos\theta ,tan\theta =cot\theta \]and \[sec\theta =cosec\theta \].
2. \[\sin \theta \] and \[tan\theta \] are increasing functions in \[0{}^\circ \le \theta \le 90{}^\circ \] {or \[\theta \in [0,\frac{\pi }{2}]\]}.

Graphically it is shown as,

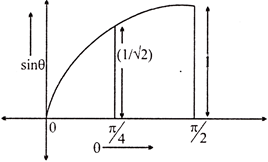
Graph of \[y=\sin \,\theta \] in \[\theta \,\in [0,\pi /2]\]

3. \[\cos \,\theta \] is a decreasing function in \[0{}^\circ \le \theta \le 90{}^\circ \] {or \[\theta \in [0,\frac{\pi }{2}]\]}

            Graphically, it is shown as,

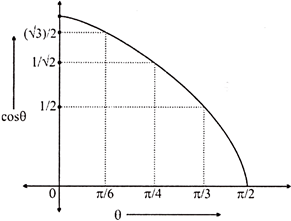
Graph of \[y=\cos \theta \] in \[\theta \in \left[ 0,\frac{\pi }{2} \right]\]