10th Class Mathematics Introduction to Trigonometry Introduction To Trigonometry

Introduction to Trigonometry

As we know, the trigonometry is the branch of Mathematics in which we study about the relationship between angles and its sides. In this chapter, we will discuss about trigonometric ratios which are defined in a right-angled triangle.

Trigonometrical Ratios

In the given triangle ABC, \[\angle B=90{}^\circ \]and let angle C is\[\theta \].

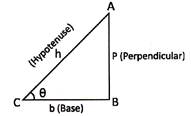
Then the trigonometrical ratios are defined as follows:

• \[\sin \theta =\frac{Perpendicular}{Hypotenuse}=\frac{AB}{AC}\]
• \[\cos \theta =\frac{Base}{Hypotenuse}=\frac{BC}{AC}\]
• \[\tan \theta =\frac{Perpendicular}{Base}=\frac{AB}{BC}\]
• \[\cot \theta =\frac{Base}{Perpendicular}=\frac{BC}{AB}\]
• \[\sec \theta =\frac{Hypotenuse}{Base}=\frac{AC}{BC}\]
• \[cosec\theta =\frac{Hypotenuse}{\operatorname{Perpendicular}}=\frac{AC}{AB}\]

Relationship between T-ratios

\[\sin \theta =\frac{1}{\operatorname{cosec}\theta },\,\,\cos \theta =\frac{1}{\sec \theta }\,\,and\,\,\cot \theta =\frac{1}{\tan \theta }\]

From the above, we conclude that sine of an angle is reciprocal to the cosec of that angle and so on.

Tringonometric Ratios of Complementary Angles

• \[\sin \,\,(90{}^\circ -\theta )=\cos \theta \]\[\frac{1}{2}\]
• \[\cos \,\,(90{}^\circ -\theta \,\,)=\,\,\sin \theta \]
• \[\tan \,\,(90{}^\circ -\theta \,\,)=\,\,\cot \theta \]
• \[\cot \,\,(90{}^\circ -\theta \,\,)=\,\,\tan \theta \]
• \[\sec \,\,(90{}^\circ -\theta \,\,)=\,\,\cos ec\theta \]
• \[\cos ec\,\,(90{}^\circ -\theta \,\,)=\,\,\sec \theta \]

Trigonometric Identities

The trigonometric ratios of an angle \[\theta \] is said to be a trigonometric identity if it is satisfied for ail values of 9 .In this chapter we will learn about following identities.

• \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
• \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
• \[cose{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]

T-ratios of Some Standard Angles        

Example:

\[\cos ec\theta -\cot \theta =a\], then the value of \[\cot \theta \]is:

(a) \[\frac{a-1}{2a}\]                  (b) \[\frac{1-{{a}^{2}}}{2a}\]

(c) \[{{a}^{2}}-1\]                    (d) \[\frac{{{a}^{2}}-1}{{{a}^{2}}+1}\]

(e) None of these

Answer (b)

Explanation: Here it is given that          … (i)

We know that, \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]

\[\Rightarrow \,\,\cos ec\theta +\cot \theta =\frac{1}{\cos ec\theta -\cot \theta }\]

\[\Rightarrow (\cos ec\theta +\cot \theta )=\frac{1}{a}\]                 … (ii)

\[\Rightarrow \cot \theta =\frac{1-{{a}^{2}}}{2a}\]

Example:

The value of \[\frac{{{\sin }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{{{\sin }^{2}}45{}^\circ }\] is:

(a) \[\frac{1}{2}\]                                   (b) \[\frac{1}{4}\]

(c) 3                              (d) 1

(e) None of these

Answer (c)

Explanation:  \[\frac{{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}+{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}}{\left( \frac{1}{\sqrt{2}} \right)}=\frac{\frac{6}{4}}{\frac{1}{2}}=\frac{12}{4}=3\]

Example:

The value of \[2({{\cot }^{2}}45{}^\circ +{{\sec }^{2}}30)\]

\[-6(ta{{n}^{2}}45{}^\circ -co{{\sec }^{2}}60{}^\circ )\]

(a) \[\frac{4}{7}\]                                   (b) \[\frac{20}{3}\]

(c) \[\frac{3}{20}\]                                 (d) \[\frac{1}{3}\]

(e) None of these

Answer (b)

Explanation: Given trigonometric expression is:

\[2(\cos {{t}^{2}}45{}^\circ +{{\sec }^{2}}30{}^\circ )\]\[-6(ta{{n}^{2}}45{}^\circ -co{{\sec }^{2}}60{}^\circ )\]

\[=2\left[ 1+{{\left( \frac{2}{\sqrt{3}} \right)}^{2}} \right]\] \[-\,\,6\left[ 1-{{\left( \frac{2}{\sqrt{3}} \right)}^{2}} \right]\]

\[=2\left[ 1+\frac{4}{3} \right]-\,\,6\,\,\left[ 1-\frac{4}{3} \right]=\frac{20}{3}\]