10th Class Mathematics Introduction to Trigonometry Trigonometry

TRIGONOMETRY

FUNDAMENTALS

• Trigonometry is the study of relationship between the sides and angles of a triangle.

Trigonometrical ratio

• Trigonometric ratio of angle in a right angled AABC are defined as follows:

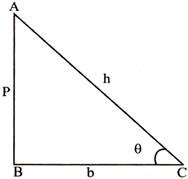
\[\sin \theta =\frac{AB}{AC}=\frac{P}{h}\]

            \[Cos\theta =\frac{AB}{AC}=\frac{b}{h}\]

            \[\tan \theta =\frac{AB}{AC}=\frac{p}{b}\]

The ratio \[\text{cosec}\theta ,\,\text{sec}\theta \] and \[\cot \theta \] are respectively the reciprocals of the \[sin\theta ,cos\theta \]and \[tan\theta .\]

i.e., \[\text{sin}\,\theta =\frac{1}{\text{cosec}\,\theta },\text{cos}\theta =\frac{1}{\sec \theta }\text{and}\,\,\text{tan}\,\theta =\frac{1}{\cot \theta }\]

Trigonometric ratio of some specific angles

• \[{{\sin }^{2}}\theta +co{{s}^{2}}\theta =1\]
• \[se{{c}^{2}}\theta -ta{{n}^{2}}\theta =1\]
• \[cose{{c}^{2}}\theta -co{{t}^{2}}\theta =1\]
• \[\sin \left( {{90}^{{}^\circ }}-\theta \right)=cos\theta ;\,\,cos\left( {{90}^{{}^\circ }}-\theta  \right)=sin\theta \]
• \[sec\left( {{90}^{{}^\circ }}-\theta \right)=cosec\theta ;\,\,cosec\left( {{90}^{{}^\circ }}-\theta  \right)=sec\theta \]
• \[tan\left( {{90}^{{}^\circ }}-\theta \right)=cot\theta ;\,\,cot\left( {{90}^{{}^\circ }}-\theta  \right)=tan\theta \]