-
question_answer1) In the given figure if \[DE\parallel BC,AE=8\,cm,\,\,EC=2cm\] and \[BC=6\,cm\], then find DE.
View Answer play_arrow
-
question_answer2) Evaluate: \[10.\frac{1-{{\cot }^{2}}45{}^\circ }{1+{{\sin }^{2}}90{}^\circ }\]
View Answer play_arrow
-
question_answer3) If cosec\[\theta =\frac{5}{4}\], find the value of \[cot\text{ }\theta \].
View Answer play_arrow
-
question_answer4)
| Following table shows sale of shoes in a store during one month: |
| Size of shoe | 3 | 4 | 5 | 6 | 7 | 8 |
| Number if pairs sold | 4 | 18 | 25 | 12 | 5 | 1 |
| Find the model size of the shoes sold. |
View Answer play_arrow
-
question_answer5) Find the prime factorisation of the denominator of rational number expressed as \[6.\overline{12}\] in simplest form.
View Answer play_arrow
-
question_answer6) Find a quadratic polynomial, the sum and product of whose zeroes are \[\sqrt{3}\] and \[\frac{1}{\sqrt{3}}\] respectively.
View Answer play_arrow
-
question_answer7)
| Complete the following factor tree and find the composite number x. |
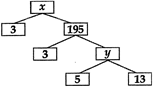 |
View Answer play_arrow
-
question_answer8) In a rectangle ABCD, E is middle point of AD. If \[AD=40\text{ }m\] and \[AB=48\text{ }m\], then find EB.
View Answer play_arrow
-
question_answer9) If \[x=p\text{ }sec\theta +q\text{ }tan\theta \] and \[y=p\text{ }tan\theta +q\text{ }sec\theta \] then prove that \[{{x}^{2}}-{{y}^{2}}={{p}^{2}}-{{q}^{2}}\].
View Answer play_arrow
-
question_answer10)
| Given below is the distribution of weekly pocket money received by students of a class. Calculate the pocket money that is received by most of the students. |
| Pocket Money (in Rs.) | 0 ? 20 | 20 ? 40 | 40 ? 60 | 60 ? 80 | 80 ? 100 | 100 ? 120 | 120 ? 140 |
| No. of Students | 2 | 2 | 3 | 12 | 18 | 5 | 2 |
View Answer play_arrow
-
question_answer11) Prove that \[3+2\sqrt{3}\] is an irrational number.
View Answer play_arrow
-
question_answer12)
| Solve by elimination: |
| \[3x=y+5\] |
| \[5x-y=11\] |
View Answer play_arrow
-
question_answer13) A man earns Rs. 600 per month more than his wife, One-tenth of the man?s salary and one-sixth of the wife?s salary amount to Rs. 1,500, which is saved every month. Find their incomes.
View Answer play_arrow
-
question_answer14) Check whether polynomial \[x-1\] is a factor of the polynomial \[{{x}^{3}}-8{{x}^{2}}+19x-12\]. Verify by division algorithm.
View Answer play_arrow
-
question_answer15) If the perimeters of two similar triangles ABC and DEF are 50 cm and 70 cm respectively and one side of\[\Delta \,ABC=20\text{ }cm\], then find the corresponding side of \[\Delta \,DEF\].
View Answer play_arrow
-
question_answer16)
| In the figure if \[DE\parallel OB\] and \[EF\parallel BC\], then prove that \[DF\parallel OC\] |
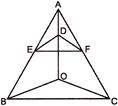 |
View Answer play_arrow
-
question_answer17) Prove the identify: \[(sec\text{ }A-cos\text{ }A)\,.\,(cot\text{ }A+tan\text{ }A)=tan\text{ }A\,.\,\,sec\text{ }A\].
View Answer play_arrow
-
question_answer18) Given \[2\,\,cos\,\,3\theta =\sqrt{3}\], find the value of \[\theta \].
View Answer play_arrow
-
question_answer19)
| For helping poor girls of their class, students saved pocket money as shown in the following table: |
| Money saved (in Rs.) | 5 ? 7 | 7 ? 9 | 9 ? 11 | 11 ? 13 | 13 ? 15 |
| Number of students | 6 | 3 | 9 | 5 | 7 |
| Find mean and median for this data. |
View Answer play_arrow
-
question_answer20)
| Monthly pocket money of students of a class is given in the following frequency distribution: |
| Pocket money (in Rs.) | 100 ? 125 | 125 ? 150 | 150 ? 175 | 175 ? 200 | 200 ? 225 |
| Number of students | 14 | 8 | 12 | 5 | 11 |
| Find mean pocket money using step deviation method. |
View Answer play_arrow
-
question_answer21) If two positive integers x and y are expressible in terms of primes as \[x={{p}^{2}}{{q}^{3}}\] and \[y={{p}^{3}}q\], what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain.
View Answer play_arrow
-
question_answer22) Sita Devi wants to make a rectangular pond on the road side for the purpose of providing drinking water for street animals. The area of the pond will be decreased by 3 square feet if its length is decreased by 2 ft. and breadth is increased by 1 ft. Its area will be increased by 4 square feet if the length is increased by 1 ft. and breadth remains same. Find the dimensions of the pond. What motivated Sita Devi to provide water point for street animals?
View Answer play_arrow
-
question_answer23) If a polynomial \[{{x}^{4}}+5{{x}^{3}}+4{{x}^{2}}-10x-12\] has two zeroes as \[-2\] and \[-3\], then find the other zeroes.
View Answer play_arrow
-
question_answer24) Find all the zeroes of the polynomial \[8{{x}^{4}}+8{{x}^{3}}-18{{x}^{2}}-20x-5,\] if it is given that two of its zeroes are \[\sqrt{\frac{5}{2}}\] and \[-\sqrt{\frac{5}{2}}\].
View Answer play_arrow
-
question_answer25)
| In the figure, there are two points D and E on side AB of \[\Delta \,ABC\] such that \[AD=BE\]. If \[DP\parallel BC\]and \[EQ\parallel AC\], then prove that \[PQ\parallel AB\]. |
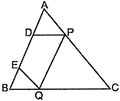 |
View Answer play_arrow
-
question_answer26)
| In \[\Delta \,ABC\], altitudes AD and CE intersect each other at the point P. Prove that |
| (i) \[\Delta \,APE\sim \Delta \,CPD\] |
| (ii) \[AP\times PD=CP\times PE\] |
| (iii) \[\Delta \,ADB\tilde{\ }\Delta \,CEB\] |
| (iv) \[AB\times CE=BC\times AD\] |
View Answer play_arrow
-
question_answer27) Prove that: \[{{(cot\text{ }A+sec\text{ }B)}^{2}}-{{(tan\text{ }B-cosec\text{ }A)}^{2}}=2(cot\text{ }A.sec\text{ }B+tan\text{ }B.cosec\text{ }A).\]
View Answer play_arrow
-
question_answer28) Prove that: \[(sin\,\theta +cos\,\theta +1).(sin\,\theta -1+cos\,\theta ).sec\,\theta \text{ }.\text{ }cosec\text{ }\theta =2\].
View Answer play_arrow
-
question_answer29)
| If \[tan\,(20{}^\circ -3\alpha )=cot\,\text{(}5\alpha -20{}^\circ )\], then find the value of \[\alpha \] and hence evaluate: |
| \[sin\text{ }\alpha \,.\text{ }sec\text{ }\alpha \,.\text{ }tan\text{ }\alpha -cosec\text{ }\alpha \text{ }.\text{ }cos\text{ }\alpha \text{ }.\text{ }cot\text{ }\alpha \]. |
View Answer play_arrow
-
question_answer30)
| The frequency distribution of weekly pocket money received by a group of students is given below: |
| Pocket money in (Rs.) | More than or equal to 20 | More than or equal to 40 | More than or equal to 60 | More than or equal to 80 | More than or equal to 100 | More than or equal to 120 | More than or equal to 140 | More than or equal to 160 | More than or equal to 180 | More than or equal to 200 |
| Number of Students | 90 | 76 | 60 | 55 | 51 | 49 | 33 | 12 | 8 | 4 |
| Draw a ?more than type? ogive and from it, find median. Verify median by actual calculations. |
View Answer play_arrow
-
question_answer31)
| Cost of living Index for some period is given in the following frequency distribution: |
| Index | 1500 ? 1600 | 1600 ? 1700 | 1700 ? 1800 | 1800 ? 1900 | 1900 ? 2000 | 2000 ? 2100 | 2100 ? 2200 |
| No. of weeks | 3 | 11 | 12 | 7 | 9 | 8 | 2 |
| Find the mode and median for above data. |
View Answer play_arrow



