-
question_answer1)
The whole surface of a rectangular block is 8788 square cm. If length, breadth and height are in the ratio of\[4:3:2\], find length.
A)
26 cm done
clear
B)
52 cm done
clear
C)
104 cm done
clear
D)
13 cm done
clear
View Solution play_arrow
-
question_answer2)
The diameters of two cones are equal. If their slant height be in the ratio \[5:7\], find the ratio of their curved surface areas.
A)
\[25:7\] done
clear
B)
\[25:49\] done
clear
C)
\[5:49\] done
clear
D)
\[5:7\] done
clear
View Solution play_arrow
-
question_answer3)
The ratio of radii of a cylinder to that of a cone is \[1:2\] If their heights are equal, find the ratio of their volumes?
A)
\[1:3\] done
clear
B)
\[2:3\] done
clear
C)
\[3:4\] done
clear
D)
\[3:1\] done
clear
View Solution play_arrow
-
question_answer4)
Find the number of bricks, each measuring\[25\,\,cm\times 12.5\,\,cm\times 7.5\,\,cm\], required to construct a wall 12m long, 5 m high and 0.25 m thick, while the sand and cement mixture occupies 5% of the total volume of wall.
A)
6080 done
clear
B)
3040 done
clear
C)
1520 done
clear
D)
12160 done
clear
View Solution play_arrow
-
question_answer5)
In a shower, 10 cm of rain falls. What will be the volume of water that falls on 1 hectare area of ground?
A)
\[500\text{ }{{m}^{3}}\] done
clear
B)
\[650\text{ }{{m}^{3}}\] done
clear
C)
\[1000\text{ }{{m}^{3}}\] done
clear
D)
\[750\text{ }{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer6)
In a swimming pool measuring 90 m by 40 m, 150 men take a dip. If the average displacement of water by a man is 8 cubic metres, what will be the rise in the water level?
A)
30 cm done
clear
B)
50 cm done
clear
C)
20 cm done
clear
D)
33.33 cm done
clear
View Solution play_arrow
-
question_answer7)
A conical tent is to accommodate 10 persons. Each person must have \[6\text{ }{{m}^{2}}\] space to sit and \[30\,\,{{m}^{3}}\] of air to breath. What will be the height of the cone?
A)
37.5 m done
clear
B)
150 m done
clear
C)
75 m done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer8)
A hollow spherical shell is made of a metal of density \[4.9g/{{m}^{3}}\]. If it?s internal and external radii are 10 cm and 12 cm respectively, find the weight of the shell. (Take \[\pi =3.1416\])
A)
5016 gm. done
clear
B)
1416.8 gm. done
clear
C)
19948.27 gm. done
clear
D)
5667.1 gm. done
clear
View Solution play_arrow
-
question_answer9)
A spherical cannon ball, 28 cm in diameter, is melted and cast into a right circular conical mould the base of which is 35 cm in diameter. Find the height of the cone correct up to two places of decimals.
A)
8.96 cm done
clear
B)
35.84 cm done
clear
C)
5.97 cm done
clear
D)
17.92 cm done
clear
View Solution play_arrow
-
question_answer10)
The areas of three adjacent faces of a cuboid are x, y, z. If the volume is V, then \[{{V}^{2}}\] will be equal to
A)
\[xy/z\] done
clear
B)
\[yz/{{x}^{2}}\] done
clear
C)
\[{{x}^{2}}{{y}^{2}}/{{z}^{2}}\] done
clear
D)
\[xyz\] done
clear
View Solution play_arrow
-
question_answer11)
The biggest possible cube is taken out of a right solid cylinder of radius 15 cm and height 25 cm respectively. What will be the volume of the cube?
A)
\[600\text{ }c{{m}^{3}}\] done
clear
B)
\[700\text{ }c{{m}^{3}}\] done
clear
C)
\[8000\text{ }c{{m}^{3}}\] done
clear
D)
\[850\text{ }c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer12)
A hemispherical bowl is filled with hot water to the brim. The contents of the bowl are transferred into a cylindrical vessel whose radius id 50% more than its height. If diameter of the bowl is the same as that of the vessel and the volume of the hot water in the cylindrical vessel is x% of the volume of the cylindrical vessel then x =?
A)
90 done
clear
B)
100 done
clear
C)
105 done
clear
D)
110 done
clear
View Solution play_arrow
-
question_answer13)
A tank internally measuring \[150\,\,cm\times 120\text{ }cm\times 100\text{ }cm\] has \[1281600\text{ }c{{m}^{3}}\]water in it Porous bricks are placed in the water until the tank is full up to its brim. Each brick absorbs one tenth of its volume of water. How many bricks, of \[20\text{ }cm\times 6\text{ }cm\times 4\text{ }cm\], can be put in the tank without spilling over the water?
A)
1150 done
clear
B)
1175 done
clear
C)
1200 done
clear
D)
1250 done
clear
View Solution play_arrow
-
question_answer14)
A spherical metal ball of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by n%. Then n =?
A)
900 done
clear
B)
800 done
clear
C)
600 done
clear
D)
200 done
clear
View Solution play_arrow
-
question_answer15)
A cap is in the shape of a right circular cone of base radius 14 cm and height 26.5 cm. The approximate area of the sheet required to make 7 such caps is
A)
\[9240\text{ }c{{m}^{2}}\] done
clear
B)
\[9420\text{ }c{{m}^{2}}\] done
clear
C)
\[8000\text{ }c{{m}^{2}}\] done
clear
D)
\[8906\text{ }c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer16)
A right circular cone is enveloping a right circular cylinder that rests on the base of the cone. If the radius and the height of the cone is 4 cm and 10 cm respectively, the radius of the cylinder is ?r? cm and the largest possible curved surface area of the cylinder is \[\text{ }\!\!'\!\!\text{ }\!\!\pi\!\!\text{ }\,\,\text{ar(b-r) }\!\!'\!\!\text{ ,}\] then \[a\times b=?\]
A)
15 done
clear
B)
20 done
clear
C)
21 done
clear
D)
24 done
clear
View Solution play_arrow
-
question_answer17)
The dimensions of a field are 20 m by 9 m. A pit 10 m long, 4.5 m wide and 3 m deep is dug in one corner of the field and the earth removed has been evenly spread over the remaining area of the field. What will be the rise in the height of field as a result of this operation?
A)
1 m done
clear
B)
2 m done
clear
C)
3 m done
clear
D)
4 m done
clear
View Solution play_arrow
-
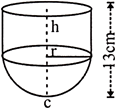
question_answer18)
A vessel is in the form of a hollow cylinder mounted on a hemispherical bowl. The diameter of the sphere is 14 cm and the total height of the vessel is 13 cm. find the capacity of the vessel. (Take \[\pi =22/7\])
A)
\[321.33\text{ }c{{m}^{3}}\] done
clear
B)
\[1642.67\text{ }c{{m}^{3}}\] done
clear
C)
\[1232\text{ }c{{m}^{3}}\] done
clear
D)
\[1632.33\text{ }c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer19)
A circular tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
A)
3894 m done
clear
B)
973.5 m done
clear
C)
1947 m done
clear
D)
1800 m done
clear
View Solution play_arrow
-
question_answer20)
A steel sphere of radius 4 cm is drawn into a wire of diameter 4 mm. Find the length of wire.
A)
10665 mm done
clear
B)
42660 mm done
clear
C)
21333 mm done
clear
D)
14220 mm done
clear
View Solution play_arrow
-
question_answer21)
A cylinder and a cone having equal diameter of their bases are placed in the form of a Minar, one over the other, with the cylinder placed at the bottom. If their curved surface areas of cylinder & cone are in the ratio of \[8:5\] respectively, find the ratio of their heights. Assume the height of the cylinder to be equal to the radius of the Minar. (Assume the Minar to be having same radius throughout).
A)
\[1:4\] done
clear
B)
\[3:4\] done
clear
C)
\[4:3\] done
clear
D)
\[2:3\] done
clear
View Solution play_arrow
-
question_answer22)
If the curved surface area of first cone is thrice that of another cone whereas slant height of the second cone is thrice that of the first, find the ratio of the area of their base.
A)
\[81:1\] done
clear
B)
\[9:1\] done
clear
C)
\[3:1\] done
clear
D)
\[27:1\] done
clear
View Solution play_arrow
-
question_answer23)
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, find the uniform thickness of the cylinder.
A)
2 cm done
clear
B)
3 cm done
clear
C)
1 cm done
clear
D)
3.5 cm done
clear
View Solution play_arrow
-
question_answer24)
A hollow sphere of external and internal radius 6 cm and 4 cm respectively is melted into a cone of base diameter 8 cm. find the height of the cone.
A)
4.75 cm done
clear
B)
9.5 cm done
clear
C)
19 cm done
clear
D)
38 cm done
clear
View Solution play_arrow
-
question_answer25)
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid (formed by adjacent placing of cubes) to that of the sum of the surface areas of the three cubes.
A)
\[7:9\] done
clear
B)
\[49:81\] done
clear
C)
\[9:7\] done
clear
D)
\[27:23\] done
clear
View Solution play_arrow
-
question_answer26)
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13 cm and 5 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if the height of conical part is 12 cm.
A)
\[1440\text{ }c{{m}^{2}}\] done
clear
B)
\[385\text{ }c{{m}^{2}}\] done
clear
C)
\[1580\text{ }c{{m}^{2}}\] done
clear
D)
\[770\text{ }c{{m}^{2}}\] done
clear
View Solution play_arrow
-
question_answer27)
A solid wooden toy is in the form of a cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of wood used in toy.
A)
\[343.72\text{ }c{{m}^{3}}\] done
clear
B)
\[266.11\text{ }c{{m}^{3}}\] done
clear
C)
\[532.22\text{ }c{{m}^{3}}\] done
clear
D)
\[133.55\text{ }c{{m}^{3}}\] done
clear
View Solution play_arrow
-
question_answer28)
A cylindrical container whose diameter is 12 cm and height is 15 cm, is filled with ice cream. The whole ice ? cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice ? cream cone. (radius of top of ice-cream cone = radius of hemisphere)
A)
6 cm done
clear
B)
12 cm done
clear
C)
3 cm done
clear
D)
18 cm done
clear
View Solution play_arrow
-
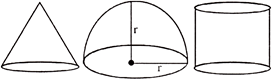
question_answer29)
A cone, a hemisphere and a cylinder stand on equal bases and have the same height what is the ratio of their volumes?
A)
\[2:1:3\] done
clear
B)
\[2.5:1:3\] done
clear
C)
\[1:2:3\] done
clear
D)
\[1.5:2:3\] done
clear
View Solution play_arrow
-
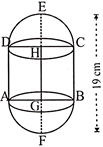
question_answer30)
A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the total surface area of the solid. (Use = 22/7)
A)
\[398.75\text{ }c{{m}^{2}}\] done
clear
B)
\[418\text{ }c{{m}^{2}}\] done
clear
C)
\[444\text{ }c{{m}^{2}}\] done
clear
D)
\[412\text{ }c{{m}^{2}}\] done
clear
View Solution play_arrow
