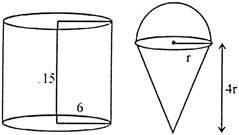
A) 6 cm
B) 12 cm
C) 3 cm
D) 18 cm
Correct Answer: A
Solution :
(a): Volume of cylindrical container \[=\pi {{(6)}^{2}}15\] Volume of ice-cream cone = volume of the cone + volume of hemispherical top \[=\frac{1}{3}\pi {{r}^{2}}4r+\frac{2}{3}\pi {{r}^{2}}=2\pi {{r}^{3}}\] (Where ?r? is the radius of the cone). \[\therefore \] \[10\times 2\pi {{r}^{3}}=\pi {{(6)}^{2}}15\] or \[{{r}^{3}}=27\] \[\Rightarrow \] \[2r=2{{(27)}^{\frac{1}{3}}}=6\,\,cm\]You need to login to perform this action.
You will be redirected in
3 sec
