Arithmetical Reasoning
Category : 9th Class
ARITHMETICAL REASONING
Learning Objectives
Introduction
This chapter includes three types of problems based on word problems Ages and Venn-diagrams.
Types of Arithmetical Reasoning
There are three types of arithmetical reasoning.
(i) Calculation on Word Problems
(ii) Problems on Ages
(iii) Venn-diagrams Problems
Calculation on Word Problems
In word problems, apply mathematical principles to the real life phenomena.
Example
(a) 35 (b) 50
(c) 64 (d) 78
(e) None of these
Answer: (c)
Explanation: Option (c) is correct. Suppose the number of girls in the class = X. i.e; the number of boys in the class =\[3\times X=3X\]
Thus, the total number of student =\[3\times X\]. Number of boys + No. of girls \[~=\text{ }X+3X=4X.\] Thus, the number of students in the class must be multiple of 4. Out of the given options only 64 is the multiple of 4. So answer is (C).
The first bunch of bananas has \[\frac{1}{4}\] excess to as many as bananas in the second bunch.
(a) 9 (b) 10
(c) 12 (d) 15
(e) None of these
Answer: (d)
Explanation: Option (d) is correct. Suppose the number of bananas in second bunch = ‘a’
Therefore, the number of bananas in first bunch \[=a+\frac{a}{4}=\frac{4a+a}{4}=\frac{5a}{4}\]
Thus, \[\frac{5a}{4}-a=3\Rightarrow 5a-4a=12\Rightarrow a=12\]
Then, number of bananas in the first bunch \[=\frac{5\times 12}{4}=15.\]
Commonly Asked Questions
(a) 36 (b) 48
(c) 56 (d) 64
(e) None of these
Answer: (b)
Explanation: Option (b) is correct. Let there be x students in the class.
When 4 students sit on each bench, number of benches \[=\left( \frac{x}{4}+3 \right)\]
When 3 students sit on each bench, number of benches \[=\left( \frac{x-3}{3} \right)\]
\[\therefore \]\[\frac{x}{4}+3=\frac{(x-3)}{3}\Leftrightarrow 3x+36=4x-12\Leftrightarrow x=48\].
Hence, number of students in the class = 48. So, the answer is (B)
(a) 35 (b) 38
(c) 40 (d) 42
(e) None of these
Answer: (b)
Explanation: Option (b) is correct. Let the number of questions attempted correctly be x. Then, number of incorrect ones \[=\left( 60-x \right)\].
\[\therefore \]\[4x-1\,(60-x)=130\Leftrightarrow 5x=190\Leftrightarrow x=38\].
Hence, the answer is (B).
(a) 106 (b) 301
(c) 309 (d) 400
(e) None of these
Answer (b)
Explanation: Option (b) is correct. Clearly, the required number would be such that it leaves a remainder of 1 when divided by 3, 4, 5 or 6 and no remainder when divided by 7. Thus, the number must be of the form
\[\left( L.C.M. of 3, 4, 5, 6 \right)\times \,\,+\,\,1\] i.e. \[\left( 60x+1 \right)\]and a multiple of 7. Clearly, for x = 5, the number is a multiple of 7. So, the number is 301.
Hence, the answer is (B).
There are 13 boys ahead of Sarita who ranked 19th the class. How many girls are in the behind Sarita?
(a) 5 (b) 6
(c) 11 (d) 12
(e) None of these
Answer (b)
Explanation: Option (b) is correct. Suppose the number of girls = a
\[\therefore \] the number of boys = 2a
Thus, a + 2a = 36 or 3a = 36
a = 36/3 = 12
Thus, there are 12 girls and 24 boys.
Number of students before Sarita = 18 and out of 18, the boys are 13 and girls are 5
So, Number of girls behind Sarita \[=12\left( 5+1 \right)=126=6\]
(a) 140 grams (b) 280 grams
(c) 240 grams (d) 120 grams
(e) None of these
Answer: (c)
Explanation: Option (c) is correct. At first time the cake was cut into two equal parts. After it one of these two parts is further cut into 6 equal parts. One small part weights 20 grams, so half cake weight \[20\times 6=120\] grams and thus the whole cake weigh \[120\times 2=240\] grams.
Problems on Ages
Example:
(a) 12 (b) 15
(c) 18 (d) 20
(e) None of these
Answer: (b)
Explanation: Option (b) is correct. Let son’s age be x then father’s age is 3x
Five years ago, father’s age = 3x – 5 and son’s age = x – 5
So, \[3x\,~5=4\text{ }\left( x5 \right)\]
\[\Rightarrow 3x5=4x~20\]
\[\Rightarrow x=15\]
How old is Reena now?
(a) 6 years (b) 12 years
(c) 10 years (d) 16 years
(e) None of these
Answer: (b)
Explanation: Option (b) is correct. Let Sunita’s present age = x years
Then Reena present age = 2x years
Three years ago
\[\left( 2x-3 \right)=3\left( x-3 \right)\]
\[2x-3=3x-9\]
or \[x=6\]
Reena age \[=2x=2\times 6=12\text{ }year\].
Commonly Asked Questions
(a) 9 years (b) 36 years
(c) 41 years (d) 51 years
(e) None of these
Answer: (c)
Explanation: Option (c) is correct. Vinay’s present age is 17 years
Five years ago, Vinay age was 12 years and that of Vikas was 36 years
Present age of Vikas = 36 + 5 = 41 years
(a) 6 years (b) 8 years
(c) 10 years (d) 12 years
(e) None of these
Answer: (b)
Explanation: Option (b) is correct Let the present age of Pushpa be x years.
Then, the present age of Rita would be (x – 2) years. Now, as given is the question.
\[X=\text{ }2\left( x22 \right)\]
or \[~x=2x8\]
or \[x=8\] years
Therefore, present age of Pushpa is 8 years.
(a) 5 years (b) 10 years
(c) 20 years (d) 30 years
(e) None of these
Answer: (c)
Explanation: Option (c) is correct. Let Chandravati's age, 10 years ago, be x years.
Then, mother's age, 10 years ago, was 4x years. After 10 years, or after 20 years when Chandravati's age would be 10 years, we have
\[\left( 4x+20 \right)=\,\,2\left( x+20 \right)\]
\[4x20=2x40\]
\[2x=20\text{ }or\text{ }x=10\] years.
Present age of Chandravati = 20 years.
(a) 25 years, 10 years (b) 36 years, 9 years
(c) 39 years, 6 years (d) All of these
(e) None of these
Answer: (b)
Explanation: Option (b) is correct. Let the present age of father be x years and that of the son be \[\left( 45x \right)\] years.
Five years ago the age of son was \[\left( 45x5 \right)=\left( 40x \right)\] and that of father was \[\left( x5 \right)\] years.
Now, \[\left( x5 \right)\left( 40x \right)=4\left( x5 \right)\text{ }{{x}^{2}}\left( 36+5 \right)x+180=0\]
or \[{{x}^{2}}-36x-5x+180=0\text{ }or\text{ }x\left( x-36 \right)-5\left( x-36 \right)=0\]
or \[\left( x-36 \right)\left( x-5 \right)=0\]
or \[~x-36-0\text{ }or\text{ }x-36\left| x \right.-5=0\text{ }or\text{ }x=5\] unacceptable
Therefore, the present age of father and son are 36 years and 9 years respectively.
(a) 20 years (b) 24 years
(c) 30 years (d) cannot be determined
(e) None of these
Answer (b)
Explanation: Option (b) is correct. Let the age of Anil and Prashant be x and (48 – x) years, respectively.
Let the age of Jayesh be y years, then
\[\left( x-y \right)=y-\left( 48-x \right)\]
or \[x-y=y-\left( 48-x \right)\]
or \[2y=48,~\,or\,~y=24\] years
\[\therefore \] Age of Jayesh is 24 years.
(A) 27 Years (b) 32 years
(c) 36 Years (q) 40 years
(E) None of these
Answer (c)
Explanation: Option (c) is correct.
Let the present age of Ashok be x years the age of Rajan = 3x years.
In 12 years hence, the age of Ashok would be (x + 12) years and that of Rajan be (3x + 12) years.
As given in the question
\[\left( 3x+12 \right)=2\left( x+12 \right)\]
or \[~3x+12=2x+24\]
or \[x=12\] years
Therefore, the age of Rajan \[=3\times 12=36\] years.
Venn-Diagram Based Problem
A Venn diagram allows us to have a pictorial representation of sets. In a Venn diagram we have a universal set U, which is represented by the region that contains everything else.
Example:

Five hundred candidates appeared in the examination conducted for the test in English, Hindi and Mathematics. The diagram gives the number of candidates who failed in different tests. What is the percentage of candidates who failed in at least two subjects?
(a) 0.078% (b) 1.0%
(c) 6.8% (d) 7.8%
(e) None of these
Answer: (d)
Explanation: Option (d) is correct. From the diagram, it is clear that number of candidates who failed in at least two subjects = number of candidates who failed in two or more subjects.
\[=\text{ }\left( 10+12+12+5 \right)=39\].
Therefore, the required percentage \[=\left( \frac{39}{500}\times 100 \right)%=7.8%\]
Therefore, the option (D) is the correct answer.
(a) 23% (b) 27%
(c) 34% (d) 40%
(e) None of these
Answer: (c)
Explanation: Option (c) is correct.
A = 42% B = 17%
C = 52%
Let the total number of students who appeared for the examination be 100 Circles a and Y represent the students who failed in Hindi and English, respectively Now number of students who failed in Hindi only.
\[=\left( 42-17 \right)\]
= 25%
Number of students who failed in English only (52 – 17) = 35%
Total number of students failed
= students failed in Hindi only + students failed in English only
= 25+35=60%.
Number of student passed = 100 – 60 = 40%
Hence, option (D) is the correct answer.
Commonly Asked Questions
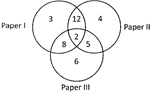
(a) 5, 000 (b) 5, 400
(c) 6, 000 (d) 6, 250
(e) None of these
Answer (b)
Explanation: Option (b) is correct. No. of persons who read at least two newspapers
= No. of persons who read two newspapers and more
\[=12+2+8+5=27\]
It means out of 50 persons 27 read at least two newspapers.
No. of such persons per\[10000=\left( \frac{27}{50}\times 10000 \right)=5400\].
(a) 18 (b) 24
(c) 21 (d) 27
(e) None of these
Answer (d)
Explanation: Option (d) is correct.
\[3,\text{ }6,\text{ }9,\text{ }...,45\]
\[a=3,\text{ }d=63=3,\text{ }n=9\]
\[{{T}_{n}}=?\]
\[=3+\left( 91 \right)\times 3=3+24=27\]
|
The following diagram shows the number of students who got distinction in there subject in a total of 500 students. Study the diagram carefully and then answer the questions that follow: |
|
|
(a) 8% (b) 9%
(c) 10% (d) 12%
(e) None of these
Answer: (a)
Explanation: Option (a) is correct. No. of students who got distinction in two subjects
\[=\left( 15+13+12 \right)=40\]
\[\therefore \] Required percentage \[=\left( \frac{40}{500}\times 100 \right)=8%\]
(a) 28% (b) 18.6%
(c) 38% (d) 15%
(e) None of these
Answer (c)
Explanation: Option (c) is correct. No. of students who got distinction
\[=\left( 50+47+42+12+11+13+15 \right)=190\]
\[\therefore \] Required percentage \[=\left( \frac{190}{500}\times 100 \right)=38%\]
(a) 17.8% (b) 18.6%
(c) 19.2% (d) 20.6%
(e) None of these
Answer: (a)
Explanation: Option (a) is correct. No. of students with distinction marks in mathematics
\[=\left( 50+13+11+15 \right)=\,\,89\]
\[\therefore \] Required percentage \[=\left( \frac{59}{500}\times 100 \right)=17.8%\]
You need to login to perform this action.
You will be redirected in
3 sec
