TRIANGLE
FUNDAMENTALS
- A closed figure formed by three intersecting lines is called a triangle
TYPES OF TRIANGLE
- Equilateral triangle:- All the three sides are equal.
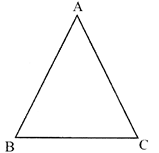
i.e., \[\angle A=\angle B=\angle C\] and also \[AB=BC=AC\]
- Isosceles triangle:- Two sides are equal.
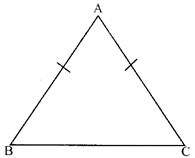
i.e., \[\angle B=\angle C\ne \angle A\] \[AB=AC\]
- Scalene triangle:- None of the three sides are equal.
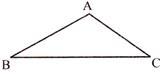
i.e., \[AB\ne BC\ne AC\]
and \[\angle A\ne \angle B\ne \angle C\]
- Acute angle triangle:- Ail the three angles are less then\[{{90}^{{}^\circ }}\]. \[\angle A,\angle B\] and \[\angle C\]are less than\[90{}^\circ \].
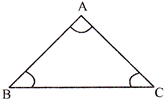
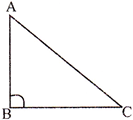
- Right angle triangle:- One Angle is equal to \[{{90}^{{}^\circ }}\] Here, \[\angle B={{90}^{{}^\circ }}\]
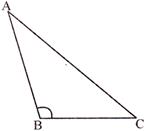
- Obtuse Angle triangle:- One of the angle greater than \[{{90}^{{}^\circ }}\], \[\angle B>{{90}^{{}^\circ }}\]
- Similar triangle:- All the angles of triangle are equal to the angles of another triangle.
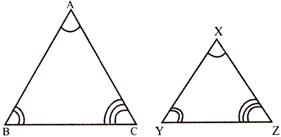
\[\angle A=\angle X\], \[\angle B=\angle Y\], \[\angle C=\angle Z\]
- Congruent triangle:- Two triangles are congruent if they are exactly same to each other in sides or angles.
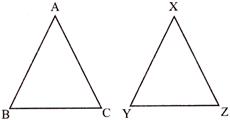
\[AB=XY\], \[BC=YZ\], \[AC=XZ\]
- Congruency conditions:- S - S - S (Side - Side - Side)
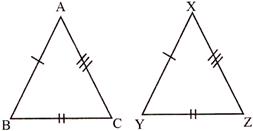
\[AB=XY,BC=YZ\] and \[AC=XZ\]
Then \[\Delta ABC\cong \Delta XYZ\]
- S - A - S (Side - Angle - Side)
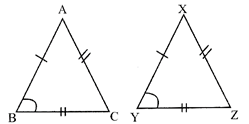
\[AB=XY\], \[BC=YZ\] and \[\angle B=\angle Y\]
Then \[\Delta ABC\cong \Delta XYZ\]
- A - S - A (Angle - Side - Angle)
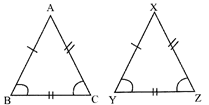
\[\angle B=\angle Y,\text{ }\angle C=\angle Z,\text{ }BC=YZ\]
Then, \[\Delta ABC\cong \Delta XYZ\]
- R - H - S (Right - Hypotenuse - Side)
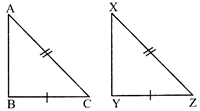
\[\angle B=\angle Y={{90}^{{}^\circ }}\] \[BC=YZ\], then \[\Delta ABC\cong \Delta XYZ.\]
SIMILARITY OF A TRIANGLE
- Two triangles are similar if their corresponding angles are equal and also their corresponding sides are in the same ratio
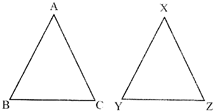
\[\Delta ABC\] and \[\Delta XYZ\] are similar if \[\angle A=\angle X,\angle B=\angle Y,\text{ }\angle C=\angle Z\] and \[\frac{AB}{XY}\text{=}\frac{BC}{YZ}=\frac{AC}{XZ}\]
- Centroid of a triangle:- Point of intersection of all the three medians.
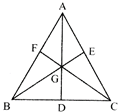
Here, Point G is centroid of triangle ABC
In Centre:- Meeting Point of all the three angle bisectors of a triangle.
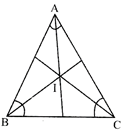
I is the in-centre of triangle ABC.
- Circum-centre:- Meeting point of the perpendicular bisectors of the perpendicular bisectors of the sides of a triangle.
- Ortho-centre:- Meeting Point of the three altitudes of a triangles.
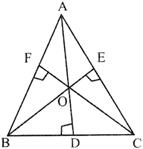
Here, Point 0 is the ortho - centre of the triangle.
PROPERTIES OF TRIANGLE
- Sum of interior angles of triangle \[{{180}^{{}^\circ }}\] and sum of exterior angles is\[{{360}^{{}^\circ }}\].
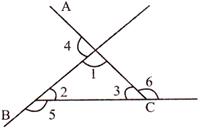
\[\angle 1+\angle 2+\angle 3={{180}^{{}^\circ }}\]
\[\angle 4+\angle 5+\angle 6={{360}^{{}^\circ }}\]
- If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
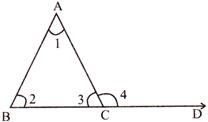
\[\angle 1+\angle 2=\angle 4\]
- If two angles of a triangles are equal, then sides opposite to them are equal.
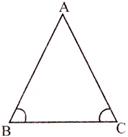
i.e., If \[\angle B=\angle C\], then \[AB=AC.\]
- If the two sides are unequal then, the longer side has the greater angle opposite to it.
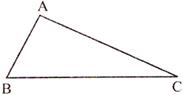
If \[AC>AB,\]
Then \[\angle B>\angle C.\]
- The sum of any two sides of mangle is greater than the third side,
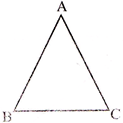
\[AB+BC>AC\]
\[AB+AC>BC\]
\[AC+BC>AB\]
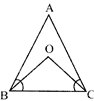
- In a \[\Delta ABC\], the bisectors of \[\angle B\] and \[\angle C\] intersect each other at a point O. Then \[\angle BOC=90+\frac{1}{2}\angle A\]
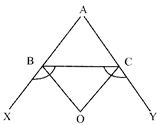
- In a triangle ABC, the sides AB and AC are produced to X and Y respectively. The bisectors of \[\angle XBC\] and \[\angle YCB\] intersect at a point 0. Then \[\angle BOC=90-\frac{1}{2}\angle A\]
- In a certain triangle ABC, \[\angle B\] is an obtuse angle and \[AD\bot BC\], then \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+2BC.CD\]
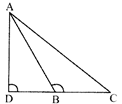
- In a certain triangle ABC \[\angle B\] is an acute angle and \[AD\bot BC\], then \[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BC.CD\]
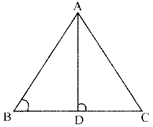
\[\angle B\] is an acute angle.
- The internal bisector of one base angle and the external bisector of the other is equal to one half of the vertical angle.
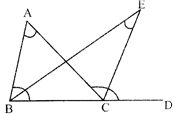
\[\angle E=\frac{1}{2}\angle A\]
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
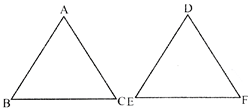
\[\frac{Area\,of\,ABC}{Area\,of\,DEF}={{\left( \frac{AB}{DE} \right)}^{2}}{{\left( \frac{BC}{EF} \right)}^{2}}{{\left( \frac{AC}{DF} \right)}^{2}}\]



























