9th Class Mathematics Triangles Congruency Figures

       Congruency Figures

Two geometrical figures are said to be congruent if they have same shape and size. e.g. two angles are said to be congruence if they have same measure similarly two line segments are said to be congruent if they have same length. In this section we will discuss about congruence of triangles.  

            Congruency of Triangles

Two triangles are said to be congruent if and only if:

(i) Their corresponding sides are equal.

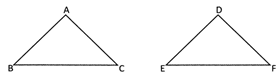
(ii) Two triangles ABC and DEF are said to be congruent if:

(a) AB = DE, BC = EF and CA = FD

(b) \[\angle \text{A}=\angle \text{D,}\,\angle \text{B}=\angle \text{E}\] and\[\angle \text{C}=\angle \text{F}\]  

            Criteria for Congruency

S-S-S Criteria

Two triangles are said to be congruent if the three sides of one triangle are equal to the correspond three sides of other.

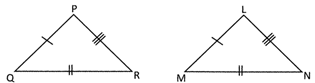
In the above given figure \[\Delta PQR\] and \[\Delta LMN\] in such a way that

\[\text{PQ}=\text{LM},\text{ QR}=\text{MN},\text{ PR}=\text{LN}\]

Then \[\Delta \text{PQR}\cong \Delta \text{LMN}\]            (Read as\[\Delta \text{PQR}\]and\[\Delta LMN\]are congruent)  

S-A-S Criteria

Two triangles are to be congruent if the two sides and included angle of one triangle is equal to the other.

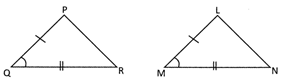
In the above given figure, \[\text{PQ}=\text{LM},\text{ QR}=\text{MN}\] and\[\angle \text{Q}=\angle \text{M}\],

Then \[\Delta \text{PQR}=\Delta \text{LMN}\]  

A-S-A Criteria

If the two angles and the side included by the angles are equal to the corresponding two angles and included sides of the other triangle then the two triangles are congruent.

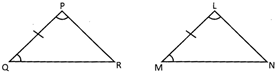
In the above given figure \[\angle P=\angle L,\angle Q=\angle M\] and \[\text{PQ}=\text{LM}\].Therefore, \[\Delta \text{PQR}\cong \Delta \text{LMN}\]  

R-H-S Criteria

This criteria is for right angle triangle. If one side and hypotenuse of a right angled triangle is equal to the corresponding side and hypotenuse of other right angled triangle then two right angled triangles are said to be congruent.

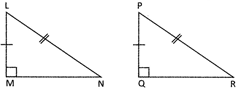
In the above given figure, LM=PQ and LN= PR, \[\angle \text{M}=\angle \text{Q}=\text{9}0{}^\circ ,\] \[\Rightarrow \] \[\Delta \text{LMN}=\Delta \text{PQR}\]