9th Class Mathematics Triangles Similar Triangles

        Similar Triangles

 

Two triangles are said to be similar if

(i) Their corresponding angles are equal and

(ii) Their corresponding sides are in proportion.

For two triangles \[\Delta ABC\] and \[\Delta PQR\]

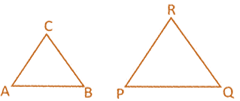
If \[\angle \text{A}=\angle \text{P},\text{ }\angle \text{B}=\angle Q\] and \[\angle C=\angle R,\] and \[\frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{PR}\]

Then \[\Delta ABC\sim \Delta PQR\]

~ : represents similarity, and the above is read as \[\Delta \]ABC is similar to \[\Delta \text{PQR}\]  

 

            Basic Proportionality Theorem or Thales Theorem

If a line is drawn parallel to any one side of a triangle intersecting the other two sides at distinct points then it divides two sides in the same ratio.  

Given: In a \[\Delta ABC\] a line I which is parallel to BC and intersect AB and AC at distinct point D and E respectively.  

To Prove:                

          \[\frac{AD}{BD}=\frac{AE}{CE}\]

 

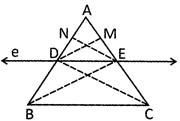
Construction:

Draw \[DM\bot AB\] and \[EN\bot AB\] and join BE, CD  

Proof:

Area of \[\Delta ADE=\frac{1}{2}\times AD\times EN\] and

Area of \[\Delta BDE=\frac{1}{2}\times BD\times EN\]

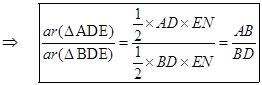              ...(i)

Similarly 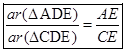                                       ...(ii)  

But \[\Delta BDE\] and \[\Delta CDE\] have the same base DE and between same parallel lines DE and BC

\[\therefore \] \[ar(\Delta BDE)=ar(\Delta CDE)\]

\[\Rightarrow \] \[\frac{ar(\Delta ADE)}{ar(\Delta BDE)}=\frac{ar(\Delta ADE)}{ar(\Delta CDE)}\]

Hence, proved  

 

            Converse of Basic Proportionality Theorem

If any line divides any two sides of a triangle in the same ratio, the line must be parallel the third side.  

 

            Criteria for Similarity

A-A-A Criteria

When two triangles are equiangular, they are said to be similar. This criteria is known as (A-A-A).

S-S-S Criteria

Two triangles are said to be similar if their corresponding sides are in proportion.

S-A-S Criteria

If one pair of corresponding sides are proportional and the included angle are equal then the triangles are said to be similar.  

 

            Theorem

The ratio of area of two similar triangles are equal to the ratio of the square of any corresponding sides.  

Given:

\[\Delta LMN\] and \[\Delta PQR\] are similar to each other.  

To Prove:        

\[\frac{ar(\Delta LMN)}{ar(PQR)}=\frac{L{{M}^{2}}}{P{{Q}^{2}}}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}=\frac{L{{N}^{2}}}{P{{R}^{2}}}\]

 

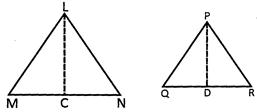
Construction:

Draw \[LC\bot MN\] and \[PD\bot QR\]  

Proof:

Since \[\Delta LMN\] and \[\Delta PQD\] are similar

\[\angle \text{L}=\angle \text{P},\text{ }\angle \text{M}=\angle \text{Q},\text{ }\angle \text{N}=\angle \text{R}\]

and \[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{LN}{PR}\]                     ... (i)

In \[\Delta \text{LMC}\] and \[\Delta \text{PQD}\], we have

\[\angle \text{LMC}=\angle \text{PQD}\]

and  \[\angle \text{LCM=}\angle \text{PDQ}=\text{9}0{}^\circ \]

\[\Rightarrow \] \[\Delta \text{LMC}\tilde{\ }\Delta \text{PQD}\]

\[\Rightarrow \]\[\frac{LM}{PQ}=\frac{LC}{PD}\]                                              ...(ii)

from (i) and (ii), we get

\[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{NL}{RP}=\frac{LC}{PD}\]

Now

\[\frac{Area\,of\,\Delta LMN}{Area\,of\,\Delta PQR}=\frac{\frac{1}{{}}\times LC\times MN}{\frac{1}{\bcancel{2}}\times PD\times QR}\]

\[\Rightarrow \]\[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{LC}{PD}\times \frac{MN}{QR}\]

\[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{MN}{QR}\times \frac{MN}{QR}\]                 \[\left[ because\frac{LC}{PD}=\frac{MN}{QR} \right]\] \[\Rightarrow \] \[\frac{ar(\,\Delta LMN)}{ar(\Delta PQR)}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}\]

but we have:

\[\frac{LM}{PQ}=\frac{MN}{QR}=\frac{NL}{RP}\]

\[\Rightarrow \] \[\frac{L{{M}^{2}}}{P{{Q}^{2}}}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}=\frac{N{{L}^{2}}}{R{{P}^{2}}}\] \[\Rightarrow \] \[\frac{ar(\Delta LMN)}{ar(\Delta PQR)}=\frac{L{{M}^{2}}}{P{{Q}^{2}}}=\frac{M{{N}^{2}}}{Q{{R}^{2}}}=\frac{N{{L}^{2}}}{R{{P}^{2}}}\]

Hence, proved  

 

            Pythagoras Theorem

In a right angled triangle, the square of hypotenuse is equal to the sum of the square of the other two sides.  

Given:

In a right angled \[\Delta \text{PQR}\] right angle at Q.  

To Prove:    

\[P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}\]

 

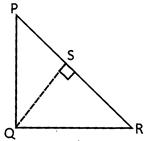
Construction:

From Q draw\[QS\bot PR\]  

Proof:        

In \[\Delta \text{PSQ}\] and \[\Delta \text{PQR}\]

\[\angle \text{P}=\angle \text{P}\]

and \[\angle \text{QSP}=\angle \text{PQR}\]

By A-A-A criteria

\[\Delta \text{PSQ}\tilde{\ }\Delta \text{PQR}\]

\[\Rightarrow \] \[\frac{PS}{PQ}=\frac{PQ}{PR}\]             \[\Rightarrow \] \[P{{Q}^{2}}=PS\times PR\]        .....(i)

In\[\Delta \text{QSR}\]and\[\Delta \text{PQR}\]

\[\angle \text{R}=\angle \text{R}\]

and   \[\angle \text{QSR}=\angle \text{PQR}=\text{9}00\]

By A-A-A criteria

\[\Delta \text{QSR}\tilde{\ }\Delta \text{PQR}\]

\[\Rightarrow \] \[\frac{SR}{QR}=\frac{QR}{PR}\]             \[\Rightarrow \] \[Q{{R}^{2}}=SR\times PR\]       .....(ii)

Adding equation (i) and (ii), we get:

\[P{{Q}^{2}}+Q{{R}^{2}}=PS\times PR+SR\times PR\]

\[\Rightarrow \] \[P{{Q}^{2}}+Q{{R}^{2}}=PR(PS+SR)\] \[\Rightarrow \] \[P{{Q}^{2}}+Q{{R}^{2}}=PR\times PR\]

\[\Rightarrow \]\[P{{Q}^{2}}+Q{{R}^{2}}=P{{R}^{2}}\]

Hence, proved  

 

            Converse of Pythagoras Theorem

In a triangle if the square of one side is equal to their sum of the square of other two sides, then the angle opposite to the side is right angle.  

 

The height of two poles are \[x\] metre and y metre respectively. If the poles are "a" metre apart then the point of intersection of the lines joining the top of each pole from opposite foot of the pole is given by..... .

(a) \[\frac{xy}{x+y}\]                                     

(b) \[\frac{x+y}{xy}\]

(c) \[\frac{1}{x}+\frac{1}{y}\]                                     

(d) \[\frac{{{x}^{2}}{{y}^{2}}}{x+y}\]

(e) None of these  

 

Answer: (a)  

Explanation:

Let AB and CD are the poles of height \[x\] metre and y metre respectively, and E is the point of intersection as required condition.

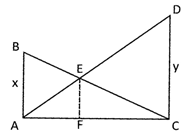
Draw \[EF\bot AC\]

In \[\Delta ABC\] and \[\Delta CFE\]

\[\angle \text{BAC}=\angle \text{EFC}\] and \[\angle \text{BCA}=\angle \text{ECA}\]

\[\Rightarrow \] \[\Delta \text{ABC}\sim \Delta \text{FCE}\]

\[\Rightarrow \] \[\frac{AB}{EF}=\frac{AC}{FC}\]

Similarly

\[\Rightarrow \]\[\Delta ACD\sim \Delta AFE\]  \[\Rightarrow \]\[\frac{CD}{EF}=\frac{AC}{AF}\]               ...(ii)

Now

Here,     AB = \[x\] metre                

               CD = y metre                

               AC = a metre

Let          AF = p metre (suppose)

\[\Rightarrow \]               \[\text{FC}=(\text{a}-\text{p)}\]metre

                      EF = h (suppose)  

Now from (i),                

\[\frac{x}{h}=\frac{a}{p}\]

\[\Rightarrow \]               \[x=\frac{ah}{p}\]

or            \[p=\frac{ah}{x}\]                             .....(i)  

Similarly from (ii)

\[\frac{y}{h}=\frac{a}{a-p}\]       \[\Rightarrow \] \[y=\frac{ah}{a-p}\]

or \[a-y=\frac{ah}{y}\]                                   .....(ii)

Adding (i) and (ii), we get:

\[a=\frac{ah}{x}+\frac{ah}{y}\]

\[\Rightarrow \] \[a=ah\left( \frac{1}{x}+\frac{1}{y} \right)\] \[\Rightarrow \] \[a=ah\left( \frac{x+y}{xy} \right)\]

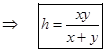
Hence, proved