| (a) \[15x{{y}^{2}},17y{{z}^{2}}\] |
| (b) \[-5{{a}^{2}}bc,11ab,13ab{{c}^{2}}\] |
| (a) Find the area of rectangular park which is \[36\frac{3}{5}\] m long and \[16\frac{2}{3}\] m broad. |
| (b) Write the name of property for any rational numbers \[\frac{a}{b}\]and\[\frac{c}{d}\], we have \[\left( \frac{a}{b}\times \frac{c}{d} \right)=\left( \frac{c}{d}\times \frac{a}{b} \right)\] |
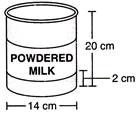
| (a) Find the population in 2001. |
| (b) What would be its population in 2005? |
| (a) \[-\frac{2}{3}\times \frac{3}{5}+\frac{5}{2}-\frac{3}{5}\times \frac{1}{6}\] |
| (b) \[\frac{2}{5}\times \left( -\frac{3}{7} \right)-\frac{1}{6}\times \frac{3}{2}+\frac{1}{14}\times \frac{2}{5}\] |
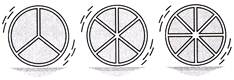
| Number of spokes | 4 | 6 | 8 | 10 | 12 |
| Angle between a pair of consecutive spokes | \[90{}^\circ \] | \[60{}^\circ \] | - | - | - |
| (a) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion? | |||||
| (b) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes. | |||||
| (c) How many spokes would be needed, if the angle between a pair of consecutive spokes is\[40{}^\circ \]? | |||||
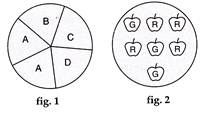
| (a) Probability of the pointer stopping on D in (figure 1) |
| (b) Probability of getting an ace from a well shuffled deck of 52 playing cards. |
| (c) Probability of getting a red apple. |
 |
| Simplify |
| (a) \[{{({{a}^{2}}-{{b}^{2}})}^{2}}\] |
| (b) \[{{(2x+5)}^{2}}-{{(2x-5)}^{2}}\] |
| (c) \[{{\left( 7m+8n \right)}^{2}}+{{\left( 7m+8n \right)}^{2}}\] |
| (d)\[{{\left( 4m+5n \right)}^{2}}+{{\left( 5m+4n \right)}^{2}}\] |
| (a) Compounded annually. |
| (b) Compounded half yearly. |
| (a) \[28{{x}^{4}}\div 56x\] |
| (b) \[-36{{y}^{3}}\div 9{{y}^{2}}\] |
| (c) \[66p{{q}^{2}}{{r}^{3}}\div 11q{{r}^{2}}\] |
| (d)\[34{{x}^{3}}{{y}^{3}}{{z}^{3}}\div 51x{{y}^{3}}{{z}^{3}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
