-
Evaluate \[\int{{{x}^{x}}(1+\log \,x)\,\,dx.}\]
View Answer play_arrow
-
The sides of an equilateral triangle are increasing at the rate of 2 cm/s. How far is the area increasing when the side is 10 cm?
View Answer play_arrow
-
Find non-zero values of x satisfying the matrix equation. \[x\left[ \begin{matrix} 2x & 2 \\ 3 & x \\ \end{matrix} \right]+2\left[ \begin{matrix} 8 & 5x \\ 4 & 4x \\ \end{matrix} \right]=2\left[ \begin{matrix} {{x}^{2}}+8 & 24 \\ 10 & 6x \\ \end{matrix} \right]\]
View Answer play_arrow
-
Find the value of \[\lambda \] such that the line \[\frac{x-2}{12}=\frac{y-1}{\lambda }=\frac{z-3}{-\,8}\] is perpendicular to the plane \[3x-y-2z=7.\]
View Answer play_arrow
-
If \[y=|x-{{x}^{2}}|,\] then find \[\frac{dy}{dx}\] at x = 1.
View Answer play_arrow
-
Find the slope and equation of the normal to \[x=1-a\sin \theta ,\] \[y=b{{\cos }^{2}}\theta \] at \[\theta =\frac{\pi }{2}.\]
View Answer play_arrow
-
Evaluate \[\int{\frac{{{e}^{x}}}{\sqrt{5-4{{e}^{x}}-{{e}^{2x}}}}dx.}\]
View Answer play_arrow
-
Find an angle \[\theta \] which increases twice as fast as its sine.
View Answer play_arrow
-
Show that all the positive integral powers of a symmetric matrix are symmetric.
View Answer play_arrow
-
Find the point on the parabola \[{{y}^{2}}=18x\] at which the ordinate increases at twice the rate of the abscissa.
View Answer play_arrow
-
Show that the three points
View Answer play_arrow
-
How many dice must be thrown so that there is a batter than even chance of obtaining a six?
View Answer play_arrow
-
| Show that |
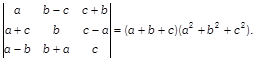 |
| OR |
If 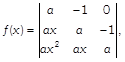 by using properties of determinants, find the value of \[f(2x)-f(x).\] by using properties of determinants, find the value of \[f(2x)-f(x).\] |
View Answer play_arrow
-
If \[y=\frac{{{\sin }^{-1}}x}{\sqrt{1-{{x}^{2}}}},\] then show that \[(1-{{x}^{2}})\frac{{{d}^{2}}y}{d{{x}^{2}}}-3x\frac{dy}{dx}-y=0.\]
View Answer play_arrow
-
Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the coordinate axes at A and B_ such that P is the mid-point of AB.
View Answer play_arrow
-
| Evaluate \[\int{\frac{1}{3{{x}^{2}}+5x+7}\,dx.}\] |
| OR |
| Evaluate \[\int{\frac{x{{e}^{x}}}{{{(x+1)}^{2}}}\,dx.}\] |
View Answer play_arrow
-
Show that \[\int_{0}^{\pi /2}{f(\sin 2x)\sin \,x\,\,dx}\] \[=\sqrt{2}\int_{0}^{\pi /4}{f(cos2x)cos\,x\,\,dx}\]
View Answer play_arrow
-
Solve the following equation. \[{{\tan }^{-1}}\sqrt{{{x}^{2}}+x}+{{\sin }^{-1}}\sqrt{{{x}^{2}}+x+1}=\frac{\pi }{2}\]
View Answer play_arrow
-
Solve the following differential equation. \[(1+{{x}^{2}})\frac{dy}{dx}-2xy=({{x}^{2}}+2)({{x}^{2}}+1),\] When x = 1 and y = 2. If y is distance and x is the time, \[\frac{dy}{dx}\] is velocity. John rides a vehicle beyond the limit on a highway. What suggestion would you give him to help understands the risks of overlapping?
View Answer play_arrow
-
Find the distance from the point (3, 4, 5) to the point, where the line \[\frac{x-3}{1}=\frac{y-4}{2}=\frac{z-5}{2}\] meets the plane \[x+y+z=2.\]
View Answer play_arrow
-
Find the probability distribution of number of doublets in three throws of a pair of dice.
View Answer play_arrow
-
Show that area of the parallelogram whose diagonals are given by \[\vec{a}\] and \[\vec{b}\] is \[\frac{|\vec{a}\,\,\times \vec{b}|}{2}.\] Also, find the area of the parallelogram whose diagonals are \[2\hat{i}-\hat{j}+\hat{k}\] and \[\hat{i}+3\hat{j}-\hat{k}.\]
View Answer play_arrow
-
| A letter is known to have come from either TATANAGAR' or 'CALCUTTA?. On the envelope just two letters ?TA? are visible. What is the probability that the letter has come from |
| (i) TATANAGAR? |
| (ii) CALCUTTA? |
| OR |
| If A and B are two independent events such that \[P(\bar{A}\cap B)=\frac{2}{15}\] and \[P(A\cap \bar{B})=\frac{1}{6},\] then find P(A) and P(B). |
View Answer play_arrow
-
| If \[f:R\to R\] is a function defined by \[f(x)=2{{x}^{3}}-5,\] then show that the function f is a objective function. |
| OR |
| Consider \[f:R\to R\] given by \[f(x)=4x+3.\]Show that f is invertible and find the inverse off. |
View Answer play_arrow
-
| The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method, |
| OR |
If 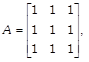 prove that prove that |
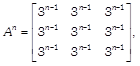 \[n\in N.\] \[n\in N.\] |
View Answer play_arrow
-
Find the area of the region bounded by \[y=-\,1,\] y = 2, \[x={{y}^{3}}\] and x = 0.
View Answer play_arrow
-
| A variable plane which remains at a constant distance 3p from the origin cut the coordinate axes at A, B and C. Show that the locus of the centroid of \[\Delta ABC\] is \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}={{p}^{-2}}.\] |
| OR |
| If the lines \[\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\] and \[\frac{x-3}{2}=\frac{y-k}{2}=\frac{z}{1}\] intersect, find the value of k and hence, find the equation of the plane containing these lines. |
View Answer play_arrow
-
A manufacturer considers that men and women workers are equally efficient, so he pays them at the same rate. He has 30 and 17 units of workers (male and female) and capital respectively, which he uses to produce two types of goods A and B, To produce 1 unit of A, 2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce 1 unit of B. If A and B are priced at Rs. 100 and Rs. 120 per unit respectively, then how should he use his resources to maximise the total revenue? Form the above as an LPP and solve it graphically. Also, write what quality of manufacturer reflects here?
View Answer play_arrow
-
Find the value of p for which the curves\[{{x}^{2}}-9p(9-y)\] and \[{{x}^{2}}=p(y\,+1)\] cut each other at right angle.
View Answer play_arrow
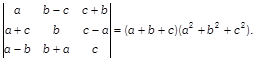
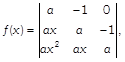 by using properties of determinants, find the value of \[f(2x)-f(x).\]
by using properties of determinants, find the value of \[f(2x)-f(x).\]  prove that
prove that 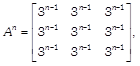 \[n\in N.\]
\[n\in N.\] 