-
If \[y={{\sin }^{-1}}(\sin \,x),\] \[x\in \left[ \frac{\pi }{2},\,\,\frac{3\pi }{2} \right],\] then evaluate \[\frac{dy}{dx}.\]
View Answer play_arrow
-
If area of a triangle with vertices (k, 0), (1, 1) and (0, 3) is 5 sq units, find the value(s) of k.
View Answer play_arrow
-
Find all the vectors of magnitude \[10\sqrt{3}\] that are perpendicular to the plane of \[\hat{i}+2\hat{j}+\hat{k}\] and \[-\,\hat{i}+3\hat{j}+4\hat{k}.\]
View Answer play_arrow
-
Evaluate \[\int_{-\pi /6}^{\pi /6}{{{x}^{3}}\,{{\cos }^{2}}x\,dx.}\]
View Answer play_arrow
-
If \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] are three vectors such that \[\vec{a}+\vec{b}+\vec{c}=0,\] prove that \[\vec{a},\,\,\vec{b}\] and \[\vec{c}\] are coplanar.
View Answer play_arrow
-
Verify Lagrange's mean value theorem for \[f(x)=\log \,\,x\] in [1, 2].
View Answer play_arrow
-
The total revenue (in Rs.) received from the sale of x units of a product is given by \[R(x)=13{{x}^{2}}+26x+15.\] Find the marginal revenue when x = 7.
View Answer play_arrow
-
If the function \[f(x)=\frac{1}{x+2},\] find the points of discontinuity of the composite function \[y=f(f(x)).\]
View Answer play_arrow
-
Using elementary transformations, find the inverse of the matrix \[\left[ \begin{matrix} 3 & 10 \\ 2 & 7 \\ \end{matrix} \right],\] if it exists.
View Answer play_arrow
-
If \[x\sqrt{1+y}+y\,\,\sqrt{1+x}=0\] and \[x\ne y,\] prove that \[\frac{dy}{dx}=\frac{1}{{{(x+1)}^{2}}}.\]
View Answer play_arrow
-
Find the probability of drawing a diamond card in each of the two consecutive draws from a well-shuffled pack of cards, if the card drawn is not replaced after the first draw.
View Answer play_arrow
-
Evaluate \[\int_{\pi /4}^{\pi /2}{\sqrt{1-\sin 2x}\,dx}.\]
View Answer play_arrow
-
Evaluate \[\int{\frac{\sin x}{\sqrt{1+\sin x}}}\,dx.\]
View Answer play_arrow
-
| If \[x,\,\,y,\,\,z\in [-\,1,\,\,1],\] such that |
| \[{{\sin }^{-1}}x+{{\sin }^{-1}}y+{{\sin }^{-1}}z=\frac{-\,3\pi }{2},\] find the value of \[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}.\] |
| OR |
| Prove that |
| \[2{{\tan }^{-1}}\left( \frac{1}{5} \right)+{{\sec }^{-1}}\left( \frac{5\sqrt{2}}{7} \right)+2{{\tan }^{-1}}\left( \frac{1}{8} \right)=\frac{\pi }{4}.\] |
View Answer play_arrow
-
| Using properties of determinants, prove the following |
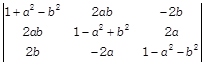 |
| \[={{(1+{{a}^{2}}+{{b}^{2}})}^{3}}.\] |
| OR |
| If x, y, z are in GP, using properties of determinants, show that |
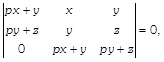 where \[x\ne y\ne z\]and p is any real number. where \[x\ne y\ne z\]and p is any real number. |
View Answer play_arrow
-
| Evaluate \[\int{(\sqrt{\tan \,\,x}\,+\,\sqrt{\cot \,x})}\,dx.\] |
| OR |
| Evaluate \[\int{{{e}^{x}}\left( \frac{1+\sin x}{1+\cos x} \right)}\,dx.\] |
View Answer play_arrow
-
Form the differential equation of the family of circles touching the X-axis at origin.
View Answer play_arrow
-
Solve \[({{x}^{3}}-3x{{y}^{2}})\,dx=({{y}^{3}}-3{{x}^{2}}y)\,dy.\]
View Answer play_arrow
-
By computing shortest distance, determine whether the following pair of lines intersect or not. \[\vec{r}=(4\hat{i}+5\hat{j})+\lambda (\hat{i}+2\hat{j}-3\hat{k})\] and \[\vec{r}=(\hat{i}-\hat{j}+2\hat{k})+\mu (2\hat{i}+4\hat{j}-5\hat{k})\]
View Answer play_arrow
-
Profit fnction of a company is given as \[P(x)=\frac{24x}{5}-\frac{{{x}^{2}}}{100}-500,\] where x is the number of units produced. What is the maximum profit of the company? Company feels its social responsibility and decided to contribute 10% of his profit for the orphanage. What is the amount contributed by the company for the charity? Justify that every company should do it.
View Answer play_arrow
-
Two cards are drawn successively without replacement from a Well-shuffled pack of 52 cards. Find the probability distribution of ace cards.
View Answer play_arrow
-
Let \[\vec{a},\,\,\vec{b}\] and \[\vec{c}\] be non-zero, non-coplanar vectors. Prove that \[\vec{a}-2\vec{b}+3\vec{c},\] \[-\,2\vec{a}+3\vec{b}\,-4\vec{c}\] and \[\vec{a}-3\vec{b}\,+5\vec{c}\] are coplanar vectors.
View Answer play_arrow
-
In a hockey match, both teams A and B scored same number of goals upto the and of the game, so to decide the winner, the referee asked both the captains to throw a die alternatively and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match.
View Answer play_arrow
-
| Let * be the binary operation on N given by a * b = LCM of a and b. Find |
| (1) 5 * 7, 20 * 16. |
| (ii) Is * commutative? |
| (iii) Is * associative? |
| (iv) Find the identity of * in N. |
| (v) Which elements of N are invertible for the operation *? |
| OR |
| Let N denote the set of all natural numbers and R be the relation on \[N\times N\] defined by d(a, b) R (c, d), if \[ad(b+c)\text{ }=\text{ }bc(a+b).\] Show that R is an equivalence relation. |
View Answer play_arrow
-
Find the area of the circle \[{{x}^{2}}+{{y}^{2}}=16,\] which is exterior to the parabola \[{{y}^{2}}=6x,\] by using integration.
View Answer play_arrow
-
| Find the image of line |
| \[\frac{x-1}{3}=\frac{y-3}{1}=\frac{z-4}{-\,5}\] in the plane \[2x-y+z+3=0.\] |
| OR |
| Find the distance of the point (3, 4, 5) from the plane \[x+y+z=2\] measured parallel to the line\[2x=y=z\]. |
View Answer play_arrow
-
David wants to invest at most Rs. 12000 in bonds A and B. According to the rule, he has to invest at least Rs. 2000 in bond A and at least Rs. 4000 in bond B. If the rates of interest on bonds A and B respectively are 8% and 10% per annum. Formulate the problem as linear programming problem and solve it graphically for maximum interest. Also, determine the maximum interest received in a year. Why investment is important for future life?
View Answer play_arrow
-
| Find the equations of tangent and normal to the curve \[y=\frac{(x-7)}{(x-2)(x-3)}\] at the point, where it cut the X-axis. |
| OR |
| Show that the equation of normal at any point on the curve x = 3 |
| \[\cos \theta -{{\cos }^{3}}\theta ,\] \[y=3\sin \theta -{{\sin }^{3}}\theta \] is |
| \[4(y\,{{\cos }^{3}}\theta -x\,{{\sin }^{3}}\theta )=3\,\sin 4\theta .\] |
View Answer play_arrow
-
If \[A=\left[ \begin{matrix} 0 & -\tan \alpha /2 \\ \tan \alpha /2 & 0 \\ \end{matrix} \right]\] and I is the identity matrix of order 2, show that \[I+A=(I-A)\left[ \begin{matrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \\ \end{matrix} \right].\]
View Answer play_arrow
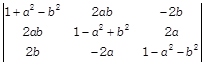
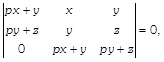 where \[x\ne y\ne z\]and p is any real number.
where \[x\ne y\ne z\]and p is any real number. 