question_answer

Find the equations of tangent and normal to the curve \[y=\frac{(x-7)}{(x-2)(x-3)}\] at the point, where it cut the X-axis.

OR

Show that the equation of normal at any point on the curve x = 3

\[\cos \theta -{{\cos }^{3}}\theta ,\] \[y=3\sin \theta -{{\sin }^{3}}\theta \] is

\[4(y\,{{\cos }^{3}}\theta -x\,{{\sin }^{3}}\theta )=3\,\sin 4\theta .\]

Answer:

Given equation of curve is

\[y=\frac{x-7}{(x-2)(x-3)}\]                                 ?(i)

To find the intersection of given curve with; X-axis.

Put y = 0 in Eq. (i), we get

\[0=\frac{x-7}{(x-2)(x-3)}\]

\[\Rightarrow \]   \[x-7=0\] \[\Rightarrow \] x = 7

Thus, the curve cut the X-axis at (7, 0).

Now, differentiating equation of curve w.r.t. x, we get

\[=\frac{(x-2)(x-3)-(x-7)(2x-5)}{{{[(x-2)(x-3)]}^{2}}}\]

\[=\frac{(x\,-2)(x\,-3)\left[ 1-\frac{(x-7)}{(x-2)(x-3)}(2x-5) \right]}{{{[(x-2)(x-3)]}^{2}}}\]     \[=\frac{1-y\,(2x-5)}{(x-2)(x-3)}\]               [using Eq. (i)]

\[\Rightarrow \]   \[{{\left( \frac{dy}{dx} \right)}_{(7,\,\,0)}}=\frac{1-0}{5\cdot 4}=\frac{1}{20}\]

Thus, slope of tangent \[=\frac{1}{20}\]

and slope of normal \[=\frac{-\,1}{\text{slope}\,\,\text{of}\,\,\text{tangent}}=-\,20\]

Hence, the equation of tangent at (7, 0) is

\[y-0=\frac{1}{20}(x-7)\] \[\Rightarrow \] \[20y-x+7=0\]

and the equation of normal at (7, 0) is \[y-0=-\,20(x-7)\] or \[20x+y-140=0.\]

OR

Given, \[x=3\cos \theta -{{\cos }^{3}}\theta \]

On differentiating both sides w.r.t. \[\theta ,\] we get

\[\frac{dx}{d\theta }=-\,3\sin \theta -3{{\cos }^{2}}\theta (-sin\theta )\]

\[=3{{\cos }^{2}}\theta \sin \theta -3sin\theta \]

\[=3\sin \theta (co{{s}^{2}}\theta -1)\]

\[[\because \,\,co{{s}^{2}}\theta +si{{n}^{2}}\theta =1]\]

\[=-\,3{{\sin }^{3}}\theta \]                                 ?(i)

and       \[y=3\sin \theta -{{\sin }^{3}}\theta \]

On differentiating both sides w.r.t.\[\theta ,\] we get

\[\frac{dy}{d\theta }=3\cos \theta -3{{\sin }^{2}}\theta \cos \theta \]

\[=3\cos \theta (1-{{\sin }^{2}}\theta )=3\cos \theta \cdot {{\cos }^{2}}\theta \]  \[=3{{\cos }^{3}}\theta \]                         ?(ii)

\[\therefore \]      \[\frac{dy}{dx}=\frac{\frac{dy}{d\theta }}{\frac{dx}{d\theta }}=\frac{3{{\cos }^{3}}\theta }{-\,3{{\sin }^{3}}\theta }=-\frac{{{\cos }^{3}}\theta }{{{\sin }^{3}}\theta }\]

Now, equation of the normal at

\[(3cos\theta -co{{s}^{3}}\theta ,3sin\theta -si{{n}^{3}}\theta )\] is

\[y-3\sin \theta +{{\sin }^{3}}\theta =-\frac{\frac{-\,1}{{{\cos }^{3}}\theta }}{{{\sin }^{3}}\theta }(x-3\cos \theta +{{\cos }^{3}}\theta )\]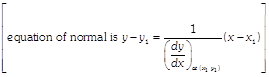

\[\Rightarrow \] \[y-3\sin \theta +{{\sin }^{3}}\theta =\frac{{{\sin }^{3}}\theta }{{{\cos }^{3}}\theta }\]

\[(x-3cos\theta +co{{s}^{3}}\theta )\]

\[\Rightarrow \] \[y{{\cos }^{3}}\theta -3\sin \theta {{\cos }^{3}}\theta +{{\sin }^{3}}\theta co{{s}^{3}}\theta \]

\[=x{{\sin }^{3}}\theta -3{{\sin }^{3}}\theta \cos \theta +{{\sin }^{3}}\theta {{\cos }^{3}}\theta \]

\[\Rightarrow \] \[y{{\cos }^{3}}\theta -x{{\sin }^{3}}\theta +3({{\sin }^{3}}\theta \cos \theta -\]

\[\sin \theta {{\cos }^{3}}\theta )=0\]

\[\Rightarrow \] \[y{{\cos }^{3}}\theta -x{{\sin }^{3}}\theta +3\sin \theta \cos \theta \]

\[({{\sin }^{2}}\theta -{{\cos }^{2}}\theta )=0\]

\[\Rightarrow \] \[y{{\cos }^{3}}\theta -x{{\sin }^{3}}\theta -\frac{3}{2}\sin 2\theta \cos 2\theta =0\]

\[[\because \,\,\,sin2\theta =2sin\theta cos\theta ,\,\,co{{s}^{2}}\theta -si{{n}^{2}}\theta =cos2\theta ]\]

\[\therefore \] \[y{{\cos }^{3}}\theta -x{{\sin }^{3}}\theta -\frac{3}{4}\sin 4\theta =0,\]

\[[\because \,\,\,sin4\theta =2sin2\theta cos2\theta ]\]

\[\therefore \] \[4(y{{\cos }^{3}}\theta -x{{\sin }^{3}}\theta )=3sin4\theta \]

Hence proved.